基于变换域形状描述子的图像检索方法的比较与分析

毛玉妃 王 斌，2 舒华忠

(1东南大学影像科学与技术实验室，南京 210096)

(2南京财经大学江苏省电子商务重点实验室，南京 210046)

基于变换域形状描述子的图像检索方法的比较与分析

毛玉妃1王 斌1，2舒华忠1

(1东南大学影像科学与技术实验室，南京 210096)

(2南京财经大学江苏省电子商务重点实验室，南京 210046)

为了更好地了解变换域方法在图像检索中的检索效果，比较分析了Zernike矩、GFD、PCET、RCFT和RFMT等现有的5种基于变换域的形状描述方法.分别在不变性、计算复杂性、噪声鲁棒性、有效特征数的选取方面对其进行了深入的分析和比较.选用MPEG7 CE Shape-1 Part B中的1 400幅图像构成的图像库对这些方法进行检索和性能测试，并实际应用于由500幅病例图构成的图像库的医学图像检索.在研究噪声影响时，对各测试集图片加上不同程度的高斯噪声.通过比较分析及实验结果验证，Zernike矩和GFD方法的检索性能最好，有良好的抗噪性，因而适合于医学图像检索的实际应用.

图像检索;形状描述;变换域分析;医学图像检索

在基于内容的图像检索中形状特征是一个很重要的方面.因为形状是刻画物体最本质及最难描述的图像特征之一.形状特征又可分为空间域特征和变换域特征.变换域具有把握图像全局特性及抵抗图像噪声等天然优点，如 DCT(discrete cosine transform)域和 DFT(discrete Fourier transform)域的能量分布集中、DWT(discrete wavelet transform)域的多分辨率分析和Zernike变换的RST(rota-tion，scale and translation)不变性等.能量分布集中意味着只需用较少的特征就能大致表示一幅图像，RST不变意味着它能很好地应用于图像检索中.目前常见的用于图像检索的变换域方法有矩技术(包括几何矩［1］、Zernike 矩［2］、Legendre 矩［3］及Fourier-Mellin 矩［4］)、DWT［5］、傅里叶算子(包括一维 FD［6］(Fourier descriptor)和二维 GFD［6］)、Radon、ART［7］(angular radial transform)等.矩技术(除几何矩)有很好的旋转不变性，而平移不变性和尺度不变性可通过对图像进行预处理实现.单独的小波和Radon变换很难实现RST不变性，但可通过将小波和Radon变换与其他变换结合使用实现RST不变性.

本文详细分析比较了Zernike矩、GFD、PCET、RCFT和RFMT等5种具有RST不变性的变换域方法.将这5种方法应用于图像检索上，并且在RST不变性、噪声鲁棒性、时间复杂度和有效特征数等方面详细比较了这5种方法在图像检索中的检索效果.最后将这些检索方法应用在医学图像检索上，验证其在医学图像检索上的有效性.

1 5种变换域形状描述方法简介

一种特征能否用于图像检索主要取决于其有无RST不变性.也就是图像经过平移、旋转及尺度变换后，该图像计算出的特征值与原图像计算出的特征值的一致程度.下面主要围绕5种方法的RST不变性上展开研究.

1.1 Zernike矩

Zernike矩因其具有优良的旋转不变性而在模式识别等领域得到广泛的应用.在图像分析中，由于Zernike多项式的正交性，可以使信息冗余达到最优.虽然Zernike矩具有旋转不变性，但却不具备尺度不变性，因此在采用Zernike矩描述形状时，首先需要进行归一化处理［2］.MPEG-7标准中已将Zernike矩列为一种标准的区域描述符.

对H×W的图像f(x，y)，Zernike矩定义如下:

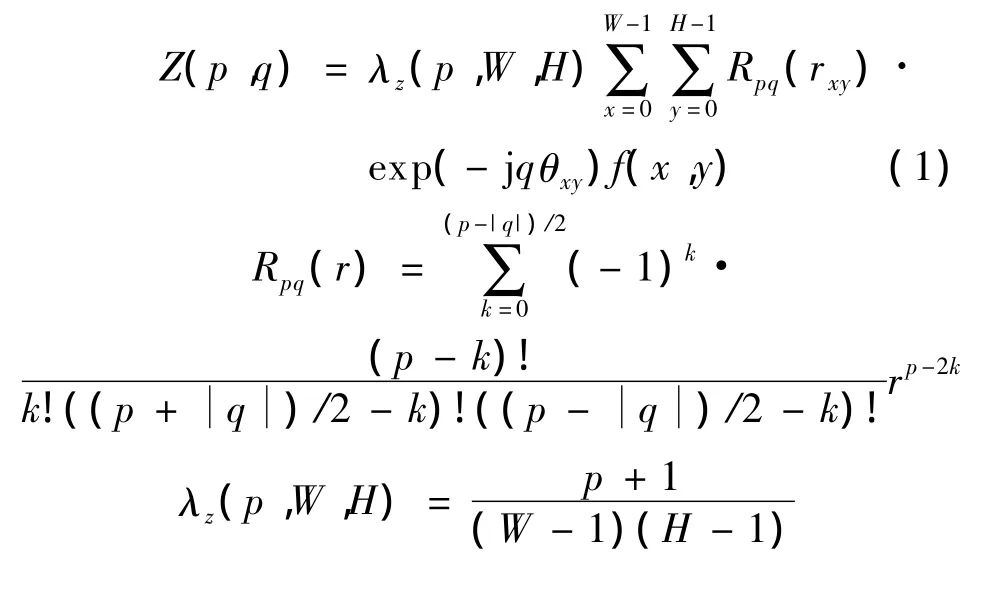
式中，p，q为整数，且为偶数;r为点(x，y)到形状质心的半径;θ为r与x轴的夹角.

Zernike矩RST不变性的实现方法如下:

1)旋转不变性 通过取Zpq模实现旋转不变.

2)平移不变性 通过将图像的质心移到图像的中点实现平移不变.

3)尺度不变性 通过除以图像的质量(即几何矩［1］m00)，实现尺度不变.

1.2 GFD

对图像直接进行二维离散傅里叶变换不具有旋转不变性，故需对图像进行一定处理.首先将GFD极坐标下的图像展开为笛卡尔坐标下的矩形图像［6］，进行极坐标变换后将图像的旋转转化为平移.然后对展开后的图像进行二维离散傅里叶变换，即可实现旋转不变.二维离散傅里叶变换式为

式中，R，T分别为径向频率分辨率和角向频率分辨率，0≤r＜R，0≤x＜T;η，φ 分别为径向频率和角向频率.

GFD方法RST不变性的实现方法如下:

1)旋转不变性 极坐标上的旋转反应在直角坐标上是平移，而平移表现在傅里叶变换上是相位的改变，故可通过取模实现旋转不变.

2)平移不变性 通过在计算时将质心设置为原点，实现平移不变.

3)尺度不变性 对计算得出的系数进行如下归一化处理，就可实现尺度不变

式中，A为转换为极坐标前的面积.

1.3 PCET

PCET方法的变换式定义［8］为

式中，Hnl(r，θ)=Rn(r)ejlθ，Rn(r)=ej2πnr2;n为阶数;l为重复度.

PCET的定义与GFD相似，仅是内核有差异.从式(4)可以看出，随着阶数的增大，GFD的特征值G趋于0，而高阶PCET特征值并不趋于0.

PCET方法实现平移不变、旋转不变与尺度不变的处理方法与GFD方法相同.

1.4 RCFT

RCFT方法是通过几种变换的组合实现RST的不变性.首先通过倒角距离变换［9］(chamfer distance transform)将一幅图像分成多幅相似的图像.然后对倒角距离变换后的每幅图像f(x，y)进行Radon变换，即

式中，δ(·)为狄拉克函数(当x=0 时，δ(x)=1，否则δ(x)=0);ρ为投影线到原点的距离;φ为投影线的方向.在Radon变换的基础上再进行RTransform［10］，即

最后，对每个Rf(φ)进行一维傅里叶变换.

由于直接对图像进行Radon变换和R-Transform，图像的许多信息会丢失.而进行倒角距离变换后，可以通过取不同的灰度得到多幅图像，这样既可以提取到轮廓信息，又能提取到内部结构信息.

RCFT方法RST不变性的实现方法如下:

1)旋转不变性 旋转表现在R-Transform上是平移变换，通过取一维傅里叶变换的模消除旋转的影响.

2)平移不变性 通过Radon变换与R-Transform共同作用实现平移不变.

3)尺度不变性 由于图像放大/缩小α倍，RTransform放大/缩小α3倍，故可实现尺度不变.

1.5 RFMT

RFMT方法［11］也是通过几种变换的组合来实现RST不变.首先将图像的质心移到图像中心以实现平移不变，然后对图像进行Radon变换(见式(5)).

在Radon变换的基础上进行Fourier-Mellin变换，即

RFMT方法RST不变性的实现方法如下:

1)旋转不变性 经Radon变换后可将旋转变换转变成平移变换，平移变换经过Fourier-Mellin计算后只表现在相位的改变上，所以可通过取模消除图像旋转的影响.

2)平移不变性 通过将图像的质心移到图像的中点，实现平移不变.

3)尺度不变性 经Radon和Fourier-Mellin变换后，尺度变换只表现在系数的改变上，故通过除以该系数就能实现尺度不变.

2 性能比较分析

以下从RST、噪声、时间复杂度、有效特征数等方面分析比较5种变换域形状描述方法的性能.

2.1 RST不变性

前面对于Zernike矩、GFD、RFMT及PCET的RST不变性分析主要是针对二值图像.对于非二值图像，灰度值的变化很容易导致图像质心的偏移，所以本文在医学图像的检索上不预先进行图像平移处理.平移不变性关键在于2幅图像的质心与图像中心的相对位置的一致，因此只要医学图像在存储时遵循一定的规范，就可以保证平移不变.

对于RCFT方法的图像平移和尺度变换表现在Radon变换上只是每个投影方向上的变化.而通过R-Transform可消除投影方向上的变化.由此可见，RCFT并不要求对图像进行事先平移，也不要求针对质心进行计算.因此RCFT方法在这方面具有独特优势.

2.2 噪声鲁棒性

对于Zernike矩和RFMT方法，噪声会引起图像质心的偏移，由此会对图像的检索产生影响.

对于GFD方法，由于其本质上是傅里叶变换，而傅里叶变换系数中的低阶反映图像的整体信息，高阶反映图像的细节信息(包括噪声)，因为本文选取的是低阶特征，所以对噪声不敏感.PCET方法与GFD方法类似，对噪声也不敏感.

RCFT方法需先对图像进行倒角距离变换，而倒角变换会受到噪声的影响.从图1可以看出，RCFT受噪声的影响较大.

图1 噪声对倒角距离变换的影响

2.3 时间复杂度

1)Zernike矩 由于涉及阶乘运算，直接计算会很耗时，故本文采用文献［12］的Zernike矩快速算法，对于N×N大小的图像，需计算O(n2×N)次乘法，O(n2×N2)次加法.

2)GFD 需计算O(N2)次乘法，O(N2)次加法.

3)PCET 需计算O(N2)次乘法，O(N2)次加法.

4)RCFT 倒角距离变换需计算O(N2)次加法，Radon变换需计算O(N2)次加法(Radon变换后图像大小为U×V).R-Transform需计算O(U×V)次乘法，V次加法.Fourier变换需计算O(U)次乘法，O(U)次加法.故RCFT的时间复杂度为O(U×V)+O(U)次乘法，O(N2)+O(U)次加法.

5)RFMT Radon需计算O(N2)次加法(Radon变换后图像大小为U×V).Fourier-Mellin矩需计算O(U×V)次乘法，O(U×V)次加法.故RFMT的时间复杂度为O(U×V)次乘法，O(N2)+O(U×V)次加法.

由上述分析可以看出，PCET的时间复杂度与GFD相同，但比Zernike矩快速算法的计算复杂度要高.对于单幅图像，RCFT与RFMT的时间复杂度相似，由Radon变换后的图像大小决定.但是由于RCFT中的倒角距离变换将图像拆分为多幅计算，因此RCFT的时间复杂度会比RFMT高几倍.

2.4 有效特征数

1)Zernike矩 当高于一定阶数后，Zernike矩的计算就不再准确，且高阶矩对噪声要比低阶矩敏感得多，所以一般使用低阶矩.本文取低于10阶的36个特征值.

2)GFD 由于GFD本质上是傅里叶变换，具有傅里叶变换的性质，因此在特征选取上阶数不能太高.本文取4个幅度频域和9个角频域，共36个频域系数.

3)PCET 由于PCET的高阶特征都可以使用，所以可以构造无穷多个RST不变的特征值.本文取阶数小于3、重复度小于12的36个特征值.

4)RCFT 经过R-Transform后，对所得值进行一维傅里叶变换.本文取倒角变换后的4幅图像(因运行时间会因图像数而明显变化，故对倒角距离变换后的图，本文只取了4个灰度级的图像)，每幅取9个傅里叶变换系数，共36个特征值.

5)RFMT 随着阶数的增加不会增加时间复杂度，因此理论上可以任选一组特征值.本文取Fourier-Mellin变换后阶数小于4、重复度小于9的36个特征值.

3 实验结果和分析

目前，常用的图像检索评估方法为由查全率和查准率定义的PVR曲线.查全率为R=a/(a+c)，查准率为P=a/(a+b).其中，a为查询到的相关图像的数目;b为查询到的不相关图像的数目;c为与检测图像相关，但没有检索到的数目.当计算出图像的查全率和查准率后，将查全率作为x轴，查准率作为y轴，则可绘制出图像检索结果的PVR曲线.

3.1 检索结果及噪声鲁棒性

图2为5种变换域方法在该测试集的平均PVR曲线图.其中选用的测试集为 MPEG7 CE Shape-1 Part B中的1 400幅图像.

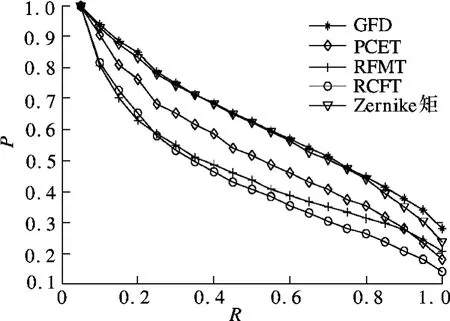
图2 各变换域方法在MPEG图像上的平均PVR曲线

实验中，2幅图像特征向量间的相似性比较采用市街区距离(city block distance).由图2可以看出，Zernike矩和GFD方法的检索效果最好，PCET次之，RFMT和 RCFT检索效果稍差.这是因为RFMT和RCFT需要几种变换才能实现RST不变性，累积离散误差比Zernike矩、GFD和PCET大.且RCFT经过R-Transform变换后会丢失很多细节信息.

对MPEG7 CE Shape-1 Part B的1 400幅图像测试集加上不同程度的高斯噪声后，各种方法的平均查准率结果见表1.

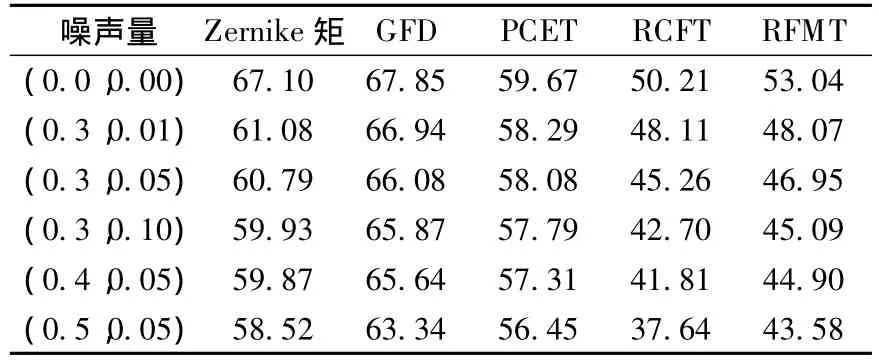
表1 加不同程度噪声后各方法的平均查准率 %

由表1可以看出，噪声对RCFT方法影响最大，其次是 Zernike矩和 RFMT，对 PCET和 GFD影响稍小.RCFT方法中由于倒角距离变换受噪声影响很大，故检索效果受噪声影响明显.由于噪声会引起图像质心的改变，因此Zernike矩和RFMT在平移图像时也易受噪声影响.

3.2 运行时间

表2为各种算法的运行时间，其中，图像为256×256像素，操作系统为Windows XP，实验平台为Visual Studio 2008，从图像提取的特征值存储在SQL Server 2005数据库中.

表2 5种变换域形状描述方法的运行时间

每种方法的运行时间是计算一组特征值所需的总时间，如计算Zernike矩的36个特征值用的总时间.RFMT算法由于Radon变换后图像变小了，因此总时间较少.而RCFT算法由于将一幅图像拆为多幅图像计算，因此所用的时间较多.

3.3 在医学图像检索中的应用

本实验的医学图像数据库是从“医影在线”网站上下载的病例，共有50种病例，每种病例包含10幅图像.当医生不能确定病例时，可以使用基于内容的图像检索，即由系统自动从图像数据库中搜索与所给样图相似的图像.这样可以根据数据库中的病例进行辅助诊断.图3为各变换域方法在医学图像上的平均PVR曲线图.

图3 各变换域方法在医学图像上的平均PVR曲线

从图3可以看出，Zernike矩和GFD的医学图像检索效果最好，而RFMT检索效果比PCET好，RCFT检索效果最差.这是因为医学图像比较复杂，而RCFT在进行倒角变换时对复杂图像影响较大，所以RCFT不适用于医学图像检索.

图4为加高斯噪声后的平均PVR曲线.从加噪声与未加噪声的对比实验可以看出，医学图像中的噪声对Zernike矩、RFMT、PCET和GFD的影响较小，但对RCFT的影响较大.

图4 加噪声后各方法在医学图像上的平均PVR曲线

4 结语

本文详细比较和分析了 Zernike矩、GFD、PCET、RFMT和RCFT 5种变换域图像检索方法，分析了它们的RST不变性、噪声鲁棒性及时间复杂度.并将这几种变换域方法用于医学图像的检索.实验结果表明，Zernike矩和GFD方法的检索效果最好，有良好的抗噪性，因而适合于医学图像检索的实际应用.

［1］Hu M K.Visual pattern recognition by moment invariant［J］.IRE Trans Information Theory，1962，8(2):179-187.

［2］Ye B，Peng J X.Analysis and improvement of invariance of Zernike moments［J］.Infrared and Laser Engineering，2003，32(1):37-41.

［3］Teh C H，Chin R T.On image analysis by the method of moments［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1988，10(4):496-513.

［4］Chao K，Mandyam D S.Invariant character recognition with Zernike and orthogonal Fourier-Mellin moments［J］.Pattern Recognition，2002，35(1):143-154.

［5］ Khalil M I，Bayoumi M M.A dyadic wavelet affine invariant function for 2D shape recognition［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2001，23(10):1152-1164.

［6］ Zhang D，Lu G.A comparative study of Fourier descriptors for shape representation and retrieval［C］//Proc5th Asian Conference on Computer Vision.Melbourne，Australia，2002:646-651.

［7］ Ricard J，Coeurjolly D，Baskurt A.Generalizations of angular radial transform for 2D and 3D shape retrieval［J］.Pattern Recognition Letters，2005，26(14):2174-2186.

［8］Yap P T，Jiang X D，Kot A C.Two-dimensional polar harmonic transforms for invariant image representation［J］.Pattern Analysis and Machine Intelligence，2010，32(7):1259-1270.

［9］ Borgefors G.Distance transformations in digital images［J］.Computer Vision，Graphics，and Image Processing，1986，34(3):344-371.

［10］ Tabbone S，Wendling L，Salmon J P.A new shape descriptor defined on the radon transform［J］.Comp Vis and Image Under，2006，102(1):42-51.

［11］ Wang X，Xiao B，Ma J F，et al.Scaling and rotation invariant analysis approach to object recognition based on Radon and Fourier-Mellin transforms［J］.Pattern Recognition，2007，40(12):3503-3508.

［12］ Gu J，Shu H Z，Toumoulin C，et al.A novel algorithm for fast computation of Zernike moments［J］.Pattern Recognition，2002，35(12):2905-2911.

Comparative study of transform domain image retrieval

Mao Yufei1Wang Bin1，2Shu Huazhong1

(1Laboratory of Image Science and Technology，Southeast University，Nanjing 210096，China)
(2Jiangsu Key Laboratory of Electronic Business，Nanjing University of Finance and Economics，Nanjing 210046，China)

In order to better understand the effect of transform domain method in image retrieval，we give a comparison of the five transform-based shape descriptors，which are Zernike moments，generic Fourier descriptor(GFD)，polar complex exponential transform(PCET)，Radon chamfer Fourier transform(RCFT)and Radon Fourier-Mellin transform(RFMT)were compared.Besides，analyses on invariance，computation complexity，noise robustness and effective number of features were conducted in detail.The five descriptors were tested by using 1 400 images from MPEG7 CE Shape-1 Part B.Furthermore，these descriptors were practically used for the medical image database including 500 images.To study the effect of the noise on retrieval，the Gaussian noise was applied to the two databases.It can be seen from the comparative analysis and the experimental results that the performance of Zernike moments and GFD are the best.They have robust noise immunity and are suitable for the practical application of medical image retrieval.

image retrieval;shape description;transform domain analysis;medical image retrieval

TP391

A

1001－0505(2012)02-0254-05

10.3969/j.issn.1001 －0505.2012.02.012

2011-12-29.

毛玉妃(1986—)，女，硕士生;舒华忠(联系人)，男，博士，教授，博士生导师，shu.list@seu.edu.cn.

国家自然科学基金资助项目(61073138，60911130370，61103141)、教育部博士点基金资助项目(20110092110023)、江苏省高校自然科学研究重大资助项目(11KJA520004).

毛玉妃，王斌，舒华忠.基于变换域形状描述子的图像检索方法的比较与分析［J］.东南大学学报:自然科学版，2012，42(2):254-258.［doi:10.3969/j.issn.1001 －0505.2012.02.012］