应用于类球体细胞电旋转分析中的介电参数求解算法

张 丽 朱晓璐 倪中华

(东南大学机械工程学院，南京 211189)

应用于类球体细胞电旋转分析中的介电参数求解算法

张 丽 朱晓璐 倪中华

(东南大学机械工程学院，南京 211189)

根据薄膜理论建立了一种面向类球体细胞的单壳介电模型，分析了细胞在电旋转静流场中的受力，并由旋转力矩和斯托克斯流体阻力矩平衡原理，推导得到细胞各层介电参数方程组.利用引入压缩因子的粒子群优化算法求解细胞的介电参数，并讨论了压缩因子的变化对求解结果的影响.以Granulocytes白细胞为例进行算法验证，得到细胞膜的电导率和相对介电常数分别为7.25 μS/m和10.3，细胞质的电导率和相对介电常数分别为0.487 S/m和136，且压缩因子的变化仅影响各组解的搜索概率，加速系数为2.015时所需解的搜索概率达到最高值.算法结果与白细胞介电参数的经验数据相吻合，表明该算法具有较高的精确性和稳定性.

介电参数;粒子群优化;电旋转;白细胞

电动旋转介电泳简称电旋转［1］，其基本原理是粒子在旋转电场中被极化产生偶极矩，并与电场相互作用而产生旋转运动.使用电旋转技术操纵、辨识和表征生物粒子的理论及应用已成为研究热点［2－4］.电旋转技术易于集成和控制，因而适用于红细胞、白细胞、酵母细胞等生物粒子的辨识、侦测和分离.已知细胞的介电参数是识别和操控细胞的前提［5］，有利于研究和分析细胞成分［6－7］.细胞在旋转电场中的旋转角速度与细胞的介电参数有关，因此，若已知细胞的电旋转定量运动规律，则可根据旋转角速度与介电参数的数值关系，得到细胞的介电参数值.国内外关于生物粒子的电旋转特性和介电参数估计的研究很多.Takashima［8］利用内部电极法和间隙法直接测量出较大生物细胞的介电性质;Asami等［9］提出应用微小吸管法来测定膜电容和膜电导;Mishima 等［6－7］发现相对介电常数增量与细胞内部包含的物质成正比，以此估计细胞内的生物质;Gascoyne等［5］采用灵敏度分析法和参数最优化法来分析电旋转数据，得到介电参数.

研究电旋转特性并间接估计细胞介电参数的工作，目前仅停留在细胞模型的建立［10］、公式推导［5，10］、测量装置的改进［11－12］等方面，对采用特定的数学方法进行参数求解的研究甚少.本文针对类球体生物细胞的电旋转数据特征，将粒子群优化方法引入到类球体细胞介电参数的求解过程中，提出了一种以改进的粒子群优化算法原理为基础的介电参数求解算法，并以Granulocytes白细胞为例，分析了计算结果.本文算法充分运用了粒子群优化的优势，大大提高了求解效率，同时降低了求解介电参数非线性方程组的难度.

1 类球体细胞模型与参数

生物细胞主要由细胞膜及内部介质(简称细胞质)构成.假设细胞质内部结构均匀，且类球体细胞的2层结构同心(见图1(a)).根据Jones的薄膜理论［10］，可将其等效为一个连续球形粒子(见图1(b)).等效后的细胞复介电常数为［10］

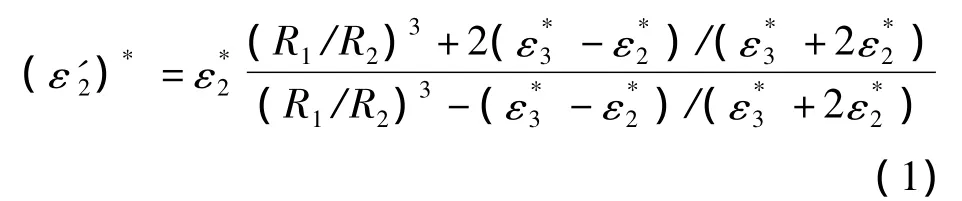
图1 类球体细胞的等效模型

式中，R1和R2分别为细胞和细胞质的半径;ε*1，ε*2，ε*3分别为流体介质、细胞膜、细胞质的复介电常数，且 ε*1= ε1－ jσ1/ω，ε*2= ε2－ jσ2/ω，ε*3=ε3－ jσ3/ω，其中 ε1，ε2，ε3分别为流体介质、细胞膜和细胞质的介电常数，σ1，σ2，σ3分别为流体介质、细胞膜和细胞质的电导率，ω为信号的角频率.

若细胞为哺乳动物细胞，且细胞膜的厚度远小于细胞半径，则其复介电常数可等效为［5］

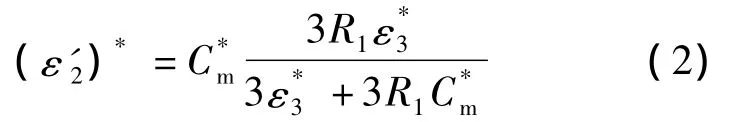
式中，C*m为细胞膜的膜电容，且C*m=ε2/Δ －jσ2/(Δω)，其中Δ为细胞膜厚度.

本文中，介电参数特指细胞膜电导率σ2、细胞膜介电常数ε2、细胞质电导率σ3和细胞质介电常数 ε3.

2 求解原理及方法

2.1 介电参数方程组的建立

将细胞放置于四相旋转电极之间，通过向4个电极分别施加相位相差90°、幅值和频率相等的信号，使细胞在偶极矩和旋转电场的相互作用下发生旋转(见图2).

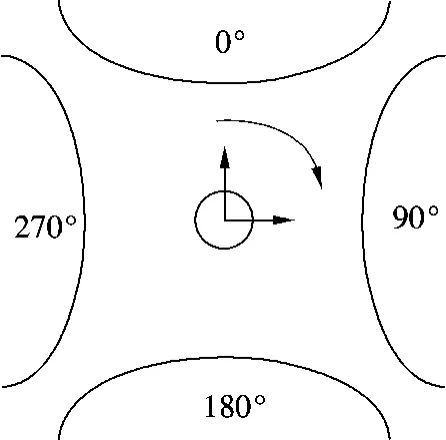
图2 电旋转电极示意图

在介电泳引起的旋转力矩及流体阻力矩的作用下，细胞匀速旋转且保持平衡.旋转力矩可表示为［10］

式中，K(ω)为克劳修斯-莫索提因子，且;E为电场强度均方根值.

由流体介质黏度产生的斯托克斯阻力矩为［5］

式中，η为流体的黏度;Ω为旋转角速度.

根据力矩平衡原理可得TDEP=TStoke.假定细胞介电参数在静流场环境中为定值，在实验中测得细胞旋转角速度Ω的频率谱，已知流体介电参数及电场规律，可建立如下的n(n＞4)维方程组:

式中，ω1，ω2，…，ωn为信号角频率;Ω1，Ω2，…，Ωn为相应的角速度.通过解此方程组，可获得细胞的介电参数.

将式(1)代入式(5)，可得超定非线性方程组，应用Matlab软件对其进行直接求解难度高且精度低.本文采用一种基于迭代的进化算法——粒子群优化(particle swarm optimization，PSO)算法［13］来求解方程组的数值解.与通用性较高的遗传算法相比，PSO算法具有更强的全局优化能力，能较快收敛，不需要考虑方程的具体组成形式，且对迭代初始点和目标函数导数的依赖性不大，适用于求解范围未知的细胞介电参数.

2.2 粒子群优化算法

PSO算法是基于群体的演化算法，源于对鸟群捕食行为的研究［13］.用PSO算法求解时，方程组介电参数的迭代解对应于鸟的位置，鸟被称为粒子.每个粒子都具有位置和速度.速度决定粒子下一次迭代的方向和前进大小.粒子位置的好坏用适应度来判定，例如对于鸟群而言，可将鸟本身与食物的距离作为捕食行动的适应度，当某一适应度为0或达到一定极限值时则捕食成功.

假设在一个D维搜索空间中，维数即为方程组未知数的个数，随机产生n个粒子(n也称为群体规模)，记第i个粒子的位置为 Xi={xi1，xi2，…，xiD}，速度为 Vi={vi1，vi2，…，viD}，其中i=1，2，…，n.将第i个粒子所经历的最佳位置称为个体极值，记为Pi={pi1，pi2，…，piD};群体中所有粒子经历的最佳位置称为全局极值，记为Gi={g1，g2，…，gD}.粒子的速度和位置可根据以下方程迭代获得［13］:

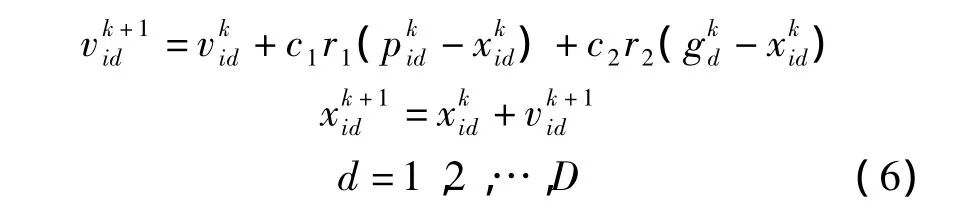
式中为第k次迭代前粒子的速度与位置;为第k次迭代后粒子的速度与位置;c1，c2为加速系数，取值范围为［0，2］;r1，r2为随机数，取值范围为［0，1］.

引入压缩因子［13］可有效地搜索不同区域，从而解决各介电参数取值范围数量级跨度大的问题，以确保PSO算法能以较快的速度收敛且得到高质量的解.相应的速度及位置迭代公式分别为

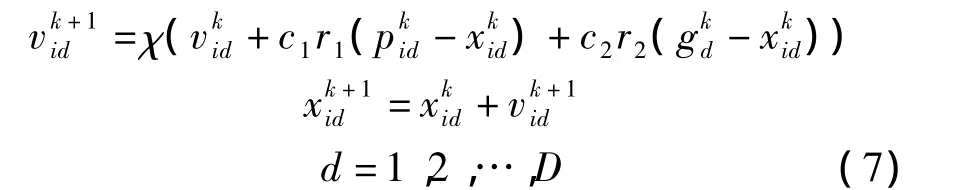
式中，χ为压缩因子，且

令欲求解的非线性方程组的一般形式为

根据PSO算法的通常处理办法［14］，定义第i个粒子的适应度函数为

式中，qj(Xi)为第j个方程代入第i个粒子后得到的实值函数.由此便可将非线性方程组的求解问题转化为minF(Xi)的最优化问题.

将PSO压缩因子法应用于求解方程组(5)，令搜索粒子的位置 Xi={σi2，εi2，σi3，εi3}，飞行速度 Vi={γi1，γi2，γi3，γi4}.根据式(7)可知，第i个粒子所对应的细胞膜电导率σi2和速度γi1的第k次迭代公式为将方程组(5)代入式(8)，得到PSO算法求解类球体细胞介电参数方程组的适应度函数，即

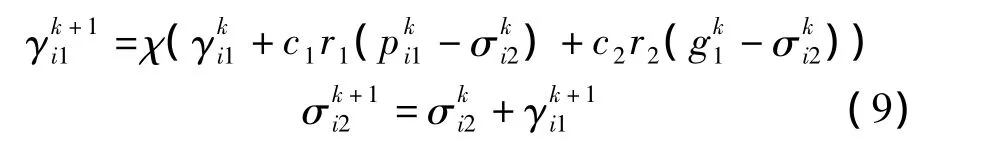
采用PSO算法求解类球体细胞介电参数的非线性方程组的步骤如下:

①确定所求介电参数的个数(即粒子维数)、粒子个数及各介电参数的数值范围.

②根据这些变量的范围，对每个粒子的介电参数(即位置)及速度进行初始化，并将每个粒子的初始介电参数作为该个体的个体极值.

③计算第i个粒子的适应度F(Xi)，并与历史最佳个体适应度以及全局最佳适应度进行比较.若F(Xi)小于历史最佳个体适应度，则将第i个粒子的介电参数作为该粒子的个体极值.同理，与全局最佳适应度比较，若F(Xi)较小，则将当前的介电参数作为全局极值.

④根据式(9)，更新粒子的介电参数和速度.

⑤如果满足结束要求，则停止迭代;否则，返回步骤③.

利用PSO算法求解非线性方程组的原理表明，当适应度越趋近于0时，得到的解越精确.为了提高算法的精确性，改进了适应度计算公式，对公式中的每一项进行1/10乘方，以避免计算时的舍入误差对适应度值产生影响.假设原适应度计算式处理后为F(X).图 3 为迭代次数N=1 000时的全局极值适应度曲线.由图可知，N＜50时适应度值下降幅度较大，N＞50时下降幅度逐渐减小，且N＞300时适应度值基本稳定不变.根据迭代法收敛性的定义，可判断该算法的收敛性:对于任意ξ＞0，该算法存在一个迭代次数K，使得对于任意大于K的迭代次数h，满足故由全局极值适应度构成的序列收敛.综上可知，采用PSO求解类球体细胞介电参数方程组的算法收敛，且收敛速度满足高效率计算的要求.

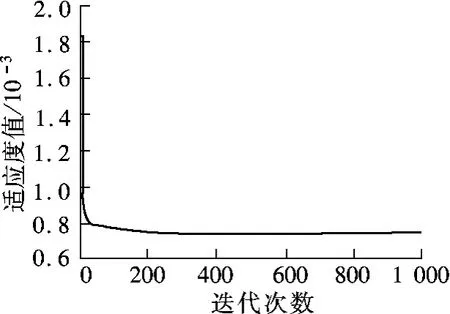
图3 全局极值适应度曲线

3 计算结果与分析

以类球体细胞Granulocytes白细胞为例，测试基于PSO的介电参数求解算法.电极形式为旋转电极;流体黏度为 0.85 mPa·s，电导率为56 mS/m，介电常数为80.2;类球体细胞的细胞半径为4.7 μm，细胞膜厚度为7.5 nm.Granulocytes白细胞的旋转角速度与频率的实验数据见图4.

设定迭代次数为1 000，粒子群体规模为20.运行算法50次，分别统计细胞膜电导率σ2、细胞膜介电常数ε2、细胞质电导率σ3以及细胞质介电常数ε3的计算结果.需要说明的是，以下统计的介电常数为相对介电常数，且各介电参数为平均值.压缩因子的取值直接影响了搜索解的能力.试凑法得到的计算结果表明，当加速系数c1，c2在2.00～2.02内取值时，方程组能获得质量较高的解.表1为算法运算50次后介电参数的统计数据.由表可知，运用本文算法可搜索到2组解，且压缩因子的取值变化仅影响搜到解的概率，不影响解的数值.

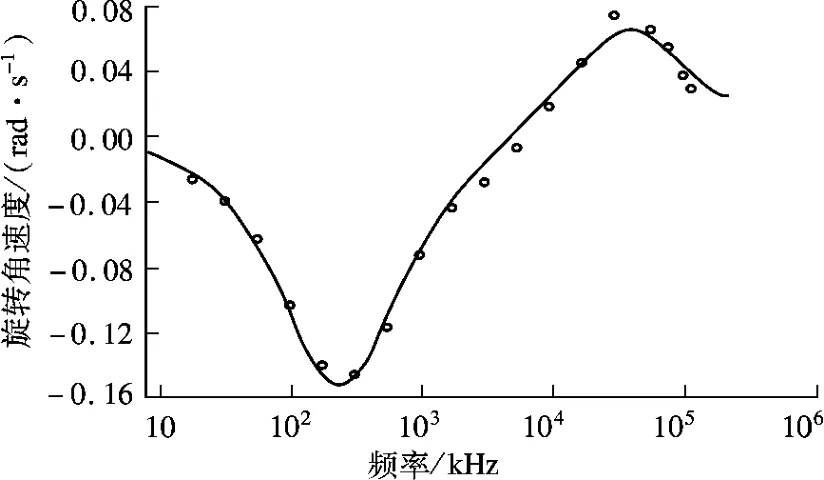
图4 Granulocytes白细胞的旋转角速度-频率实验曲线［4］

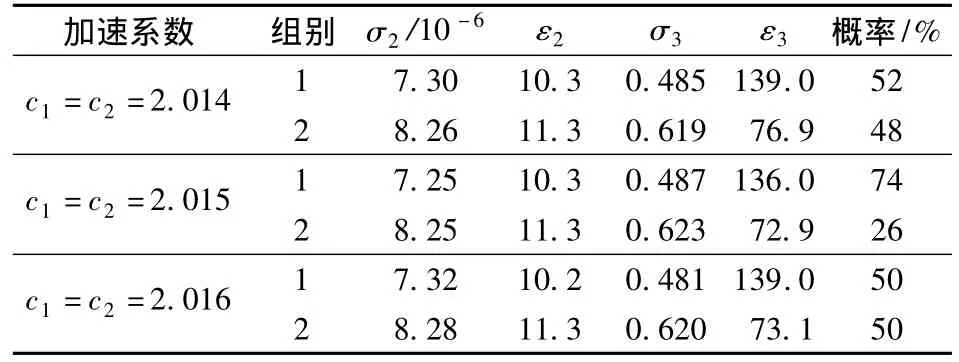
表1 介电参数的统计结果

对于单壳模型而言，典型的生物粒子介电参数范围为［5］:5 mF/m2＜Cm＜35 mF/m2，20 S/m2＜Gm＜2 000 S/m2，0.1 S/m ＜σ3＜1.3 S/m，50ε0＜ε3＜150ε0，其中Cm= ε2/Δ 为膜电容，Gm= σ2/Δ为膜电导，ε0为真空介电系数.表1所列2组解均满足上述范围.

为了进一步验证本文算法的稳定性，考察了c1，c2取值不同时算法运算50次2组解的分布情况(见图5).由图5(a)可知，细胞膜电导率主要分布在4～10 μS/m范围内，σ2的2组解范围有交集;细胞膜介电常数及细胞质电导率分布较聚集，且基本不存在交叉的现象;细胞质介电常数的第1组解分布集中，第2组解分布跨度较大，但2组数值没有交叉.比较4个介电参数发现，细胞膜电导率和细胞质介电常数的分布跨度较大，由此可推测，实验中这2个参数的取值在一定范围内对类球体细胞的速度影响不大.相比之下，细胞膜介电常数和细胞质电导率更能体现细胞的介电特性.对比图5(b)和(c)发现，压缩因子的取值仅影响各组解的聚集情况及搜索解的概率.

根据数值分析的理论定义，一个算法的输入数据有扰动，但计算过程中误差不增长，则称此算法是数值稳定的.在本文算法中，c1，c2取值变化时计算结果基本不变.因此，运用 PSO求解 Granulocytes白细胞介电参数的算法是数值稳定的.

图5 2组解的分布情况

文献［4］列出了Granulocytes白细胞介电参数的经验数据，即细胞半径为(4.71±0.23)μm，膜电容为(11.0±3.2)mF/m2，细胞质电导率为(0.60±0.13)S/m，细胞质介电常数为150.9±39.3.将这些数据作为判定本文算法正确性的依据.经计算可得ε2为9.32±2.71，比较计算结果可知，第1组解符合经验数据的取值范围，第2组解中细胞质的介电常数低于经验数据.第1组解的波动范围较小，取值较为集中，若以序列来表征50次计算的结果，则第1组解的方差显然小于第2组解，故第1组解更精密.综上可知，基于PSO的介电参数求解算法解得Granulocytes白细胞介电参数的最优解为第1组解.当c1=c2=2.015时，取搜索概率较高的第1组解，则细胞膜电导率为7.25 μS/m，细胞膜相对介电常数为10.3，细胞质电导率为0.487 S/m，细胞质相对介电常数为136，符合经验数据.因此，运用PSO求解Granulocytes白细胞介电参数的算法是精确的.

4 结语

本文描述一种基于PSO的类球体细胞介电参数求解算法.研究结果表明，引入压缩因子的PSO介电参数求解算法具有较好的收敛性，计算效率高，不依赖介电参数方程组形式且灵活性大，通过选择合适的压缩因子可获得高质量的解.以类球体细胞Granulocytes白细胞为例，在电旋转电极形式下，采用PSO算法求解介电参数方程组，可成功得到符合白细胞经验数据的计算解，即细胞膜电导率为7.25 μS/m，细胞膜相对介电常数为10.3，细胞质电导率为0.487 S/m，细胞质相对介电常数为136.因此，基于PSO的介电参数求解算法可有效地估算出类球体细胞的介电参数，这对研究未知生物粒子的性能具有重要意义.如何改进算法以及将其应用于椭球体等其他形状的生物细胞是进一步研究的重点之一.

［1］ Arnold W M，Zimmermann U.Electro－rotation:development of a technique for dielectric measurements on individual cells and particles［J］.Journal of Electrostatics，1988，21(2/3):151－191.

［2］ Sancho M，Martínez G，Muñoz S，et al.Interaction between cells in dielectrophoresis and electrorotation experiments［J］.Biomicrofluidics，2010，4(2):1－11.

［3］ Voyer D，Frénéa－Robin M，Buret F，et al.Improvements in the extraction of cell electric properties from their electrorotation spectrum ［J］.Bioelectrochemistry，2010，79(1):25－30.

［4］ Yang J，Huang Y，Wang X，et al.Dielectric properties of human leukocyte subpopulations determined by electrorotation as a cell separation criterion［J］.Biophysical Journal，1999，76(6):3307－3314.

［5］Gascoyne P R C，Becker F F，Wang X B.Numerical analysis of the influence of experimental conditions on the accuracy of dielectric parameters derived from electrorotation measurements［J］.Bioelectrochemistry and Bioenergetics，1995，36(2):115－125.

［6］ Mishima B，Mimura K A，Takahara Y，et al.On－line monitoring of cell concentrations by dielectric measurements［J］.Journal of Fermentation and Bioengineer-ing，1991，72(4):291－295.

［7］Harris C M，Todd R W，Bungard S J，et al.Dielectric permittivity of microbial suspensions at radio frequencies:a novel method for the real－time estimation of microbial biomass［J］.Enzyme Microb Technol，1987，9(3):181－186.

［8］ Takashima S.Passive electrical properties and voltage dependent membrane capacitance of single skeletal muscle fibers［J］.Pflugers Arch Eur J Physiol，1985，403(2):197－204.

［9］ Asami K，Takashima S.Membrane admittance of cloned muscle cells in culture:use of a micropipette technique［J］.Biochim Biophys Acta，1994，1190(1):129－136.

［10］ Jones T B.Basic theory of dielectrophoresis and electrorotation ［J］.IEEE Engineering in Medicine and Biology Magazine，2003，22(6):33－42.

［11］Gawad S，Cheung K，Seger U，et al.Dielectric spectroscopy in a micromachined flow cytometer:theoretical and practical considerations［J］.Lab Chip，2004，4(3):241－251.

［12］Holmes D，Green N G，Morgan H.Microdevices for dielectrophoretic flow－through cell separation ［J］.IEEE Engineering in Medicine and Biology Magazine，2003，22(6):85－89.

［13］杨维，李歧强.粒子群优化算法综述［J］.中国工程科学，2004，6(5):87－94.

Yang Wei，Li Qiqiang.Survey on particle swarm optimization algorithm ［J］.Engineering Sciences，2004，6(5):87－94.(in Chinese)

［14］陈长忆，叶永春.基于粒子群算法的非线性方程组求解［J］.计算机应用与软件，2006，23(5):137－139.

Chen Changyi，Ye Yongchun.Solving nonlinear systems of equations based on particle swarm optimization［J］.Computer Applications and Software，2006，23(5):137－139.(in Chinese)

Dielectric parameter solving algorithm in electrorotation analysis of spherical cells

Zhang Li Zhu Xiaolu Ni Zhonghua
(School of Mechanical Engineering，Southeast University，Nanjing 211189，China)

A dielectric model with single concentric shell of spherical cells is established based on film theory.The forces of the cells in a static flow field under the action of electrorotation are analyzed，and the force equilibrium equations are derived to obtain dielectric parameters of each shell by the balance of the rotating torque and the Stokes fluid drag torque.Then，the particle swarm optimization algorithm improved with the constriction factor is used to solve the equations.The influence of the change in the constriction factor on the solution results is also discussed.This algorithm is validated with Granulocytes as an example.The calculated membrane conductivity，membrane relative permittivity，cytoplasm conductivity and cytoplasm relative permittivity are 7.25 μS/m，10.3，0.487 S/m and 136，respectively.Besides，the change in the constriction factor just affects the search probability of each solution，and the search probability needed gets the highest value with the acceleration factor of 2.015.The calculated results are consistent with the empirical data，showing that the proposed algorithm can obtain high accuracy and stability.

dielectric parameter;particle swarm optimization;electrorotation;leukocyte

TP391

A

1001－0505(2012)02－0280－06

10.3969/j.issn.1001－0505.2012.02.017

2011－09－25.

张丽(1987—)，女，硕士生;倪中华(联系人)，男，博士，教授，博士生导师，nzh2003@seu.edu.cn.

国家自然科学基金重大研究计划(培育)资助项目(91023024)、教育部博士研究生学术新人奖资助项目、江苏省普通高校研究生科研创新计划资助项目(CX10B_062Z)、东南大学优秀博士学位论文基金资助项目.

张丽，朱晓璐，倪中华.应用于类球体细胞电旋转分析中的介电参数求解算法［J］.东南大学学报:自然科学版，2012，42(2):280－285.［doi:10.3969/j.issn.1001－0505.2012.02.017］