基于弹塑性理论带肋填砂管桩承载力的研究与应用
2012-09-16戴庆斌
戴庆斌
(温州职业技术学院 后勤基建处, 浙江 温州 325035)
基于弹塑性理论带肋填砂管桩承载力的研究与应用
戴庆斌
(温州职业技术学院 后勤基建处, 浙江 温州 325035)
带肋填砂管桩是对普通预应力混凝土管桩改进后形成的一种新的管桩应用类型。基于弹塑性理论的带肋填砂管桩沉降计算方法,既考虑桩身在荷载传递作用下的弹性压缩沉降,也考虑桩端以下土层的弹性和弹塑性变形沉降,并给出端阻力和桩侧阻力的分配系数确定方法。根据该模型计算结果,可进一步分析有关数据的特点及其产生的原理。结果表明,该模型的计算结果与实测结果较吻合,具有一定的应用价值。
带肋填砂管桩;承载力;沉降;侧阻力;弹塑性
0 引 言
普通预应力混凝土管桩在软土地区由于受到长细比及桩身接头数量等限制,单桩承载力不高,桩身混凝土强度无法得到充分运用而造成浪费。带肋填砂管桩作为一种对预应力混凝土管桩改进的桩型,是在普通预应力混凝土管桩桩身上加装钢肋,在沉桩施工过程中不断在肋间填筑粗砂,让粗砂充满肋间的空隙,在“硬”的桩身与“软”的桩侧软土间填入“过渡”的砂子,增加桩身的摩擦力,提高桩的承载力,充分发挥桩身混凝土的利用率[1]。带肋填砂管桩已在温州大学新校区信息行政中心工程和温州新亚电子有限公司厂房工程中应用,效果良好。这两个工程的桩基静载荷试验结果表明,带肋填砂管桩的承载力比起普通预应力混凝土管桩有较大的提高[2]。带肋填砂管桩根据静载荷试验中测得的各级加载下桩身各断面的轴力,换算出不同深度土层在各级加载下侧阻力值变化曲线,如图1所示。
1 带肋填砂管桩的沉降构成
带肋填砂管桩由于桩肋和填砂作用,一方面扩大了桩身与土层的接触面;另一方面由于粗砂对软土的改良作用,也提高了软土的侧阻力[3]。因此,带肋填砂管桩的桩身截面轴力与普通管桩相比要大很多。桩基在桩顶荷载作用下会产生沉降,在不考虑桩身缺陷的情况下,带肋填砂管桩的沉降,由在外力作用下的桩身压缩沉降以及桩侧阻力和端阻力作用下桩端以下土层压缩沉降构成。

图1 不同深度土层在各级加载下侧阻力值变化曲线
2 桩端以下持力层沉降的计算
桩基载荷通过桩身摩擦和桩端作用将荷载传递到桩侧和桩端以下土层中,致使土层中产生附加应力并产生应变,这些应变可根据土层附加应力的大小进行判别计算。根据各土层计算点处于的应力状态分别利用弹性模型和弹塑性模型计算应变,进而计算出各土层的沉降量。
2.1 桩端以下土层附加应力
根据Geddes的假设,桩基桩顶竖向荷载作用分别由桩侧阻力和端阻力(记为Pb)来承担,且侧阻力可大致呈上小下大的直角梯形分布[4]。为便于计算,可将侧阻力分为沿桩侧呈矩形均匀分布的侧阻力(记为Ps)和呈正三角分布的侧阻力(记为Pt),如图2所示。设Pb= αP,Ps=βP,Pt=γP,其中α,β,γ分别为桩端阻力、桩侧均布阻力和桩侧三角形侧阻力的荷载比例系数,γ=1-α-β。
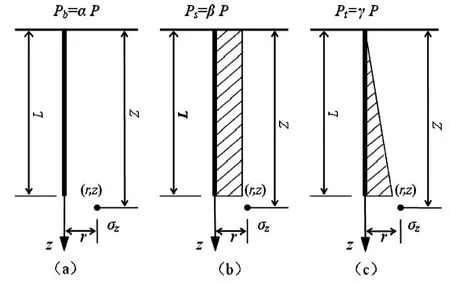
图2 单桩荷载分解
桩基在桩顶荷载作用下,桩端以下某点(r,z)处的应力可分别记为σr,σz,σθ,τrz,各应力相对应的计算公式分别为:

其中,L为单桩桩长,单位为m;Izb,Izs,Iz分别为Pb,Ps,Pt作用下土体某点(r,z)的z向(竖向)附加应力系数;Irb,Irs,Irt分别为Pb,Ps,Pt作用下土体某点(r,z)的r向附加应力系数;Iθb,IθS,Iθt分别为Pb,Ps,Pt作用下土体某点(r,z)的θ向附加应力系数;Irzb,Irzs,Irzt分别为Pb,Ps,Pt作用下土体某点(r,z)的附加剪应力系数。附加应力系数计算公式可参考文献[5]。在Pb,Ps,Pt作用下,利用叠加原理可计算出土体内任意点(r,z)处的三向附加应力。
2.2 端阻—侧阻荷载构成比例
对桩基来说,影响桩端阻力与侧阻力构成比例的因素很多,实际计算时只需考虑主要影响因素,这样计算出的结果往往会与实际有差异,当这种差异在可接受范围内,这种方法就会有利用价值。文献[6]根据刚性桩与桩侧土体协调变形原理构造出了求解桩基端阻—侧阻荷载分配系数的理论公式,但该理论公式未能区分不同土层特性、不同受力特点等对荷载分配影响较大的因素,这就使得理论公式求解出的结果与工程实际差异很大。本文采取数值拟合的方法对温州大学行政信息中心工程的试桩在各级荷载作用下实测得到的桩侧阻力数值进行拟合分析,寻找带肋填砂管桩端阻—侧阻构成比例与桩顶荷载之间的关系。其比例系数与桩顶荷载之间的拟合结果如图3所示。

图3 端阻—侧阻比例系数与桩顶荷载之间的关系
比例系数α,β,γ与桩顶荷载P的函数关系为:


其中,P为桩顶荷载,单位为KN;α,β,γ分别为桩端阻力、桩侧均布阻力和桩侧三角形侧阻力的荷载比例系数,γ=1-α-β。
3 基于弹塑性理论桩端以下土层沉降的计算
桩端以下土层属于正常固结土,假设其符合修正剑桥模型的屈服准则,将有关参数代入屈服函数F中,并判断各土层的弹塑性状态。如果该点处于屈服面以内或正好处于屈服面上,表明该点还处于弹性状态,该分土层只产生弹性变形。则该分土层在外力作用下的弹性应变增量为:

其中,Et为土层弹性模量,单位为Pa;v为泊松比;Δσz,Δσr,Δσθ分别为z,r,θ的向应力增量。
如果该点处于屈服面以外,表明该点处于弹塑性状态,该分土层既产生弹性变形,又产生塑性变形,则该土层在外力作用下的弹塑性应变增量为:

其中[D]ep为弹塑性模量矩阵。
计算桩端以下土层沉降时,将每一自然土层细分成厚度更小的分土层,根据计算精度要求不同,每一分土层的厚度也不一样,计算厚度越小表明计算精度越高。每一分土层的沉降量即为代表该土层的计算点的应变乘上该分土层厚度,在计算深度范围内,所有分土层的沉降量之和即为桩端以下卧土层沉降量Sb。计算深度的确定一般可采取设定一个桩端以下各分土层压缩沉降量限值。当往下计算各分土层沉降量时,如果分土层沉降量小于设定的限值时,即认为该土层以下土层在附加应力作用下的沉降量已经很小,可忽略不计。特别要注意的是,如果桩端以下下卧土层呈上硬下软分布时,计算深度一定要延伸到软的土层内。
4 荷载传递法桩身压缩沉降的计算
为了便于计算桩身压缩沉降,先将桩身划分成若干段,划分时要注意在不同土层交界面处即桩段的分界面,各分段长度可相等,也可不相等。
单桩在桩顶荷载作用下,桩身各截面的轴力由于桩—土共同作用的影响大小各不相同,桩—土间的荷载传递特征可用一双曲线函数近似地描述[7]。第i(i-1)段桩身的压缩沉降量如图4所示。
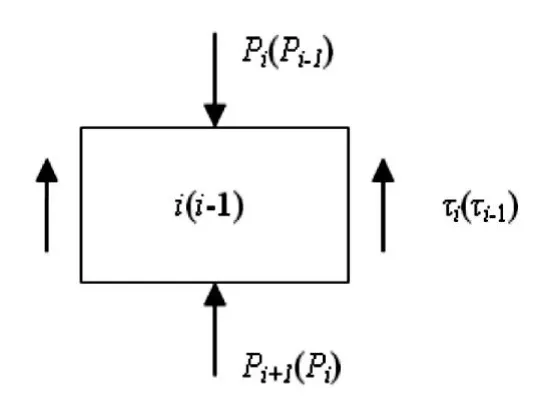
图4 第i(i-1)段桩身的压缩沉降量
根据桩—土传递双曲线函数可推导出桩侧阻力τi为:

其中,τu.i为第i土层与桩间的摩擦侧阻力的屈服值,单位为Pa;Su.i为第i土层侧阻力达到屈服值时所对应位移,单位为mm;Si+1为第i段桩身下截面土层位移,单位为mm;αi为第i桩侧土层在外力作用下屈服时所对应的土层侧阻力与土层所能达到的理论上最大侧阻力的比值,即,其中τlim.i为第i土层与桩间的摩擦侧阻力极大值,单位为Pa。
第i段轴力增量ΔPi、上截面轴力Pi和平均轴力分别为:

其中,U为桩身周长,li为第i段桩身长度,单位为mm;Pi+1为第i段桩身下截面轴力,单位为N。
第i段位移增量ΔSi、位移Si和平均位移分别为:

其中,E为桩身混凝土弹性模量,单位为Pa;A为桩身混凝土截面面积,单位为mm2;Si+1为第i段桩身下截面土层位移,单位为mm。
计算过程中假定第i分段的桩侧阻力沿桩身是均匀分布的,但实际上桩身不同深度处的侧阻力沿桩身的分布并不均匀。为提高计算精度,可将把前面计算得到的Pi,ΔSi,Si分别进行迭代计算。ΔPi可按(17)式重新计算后再代入(13)式中替换ΔPi,直至前后两次计算出的ΔPi与ΔPi'(或ΔSi与ΔSi')的差值满足要求为止。

计算桩身压缩沉降量时,应先从最下端的桩身(记为第n段)开始,第n段桩身下截面Pn和Sn即为桩端阻力Pb和桩端以下土层沉降量Sb;然后再将第n段计算的结果Pn-1,ΔSn-1,Sn-1分别当作第n-1分段桩身下断面轴力(见图4)。以此类推,可计算出位于桩基最顶端的第1段桩底轴力和桩段沉降位移P1,S1,而S1就是桩基在桩顶荷载P作用下的桩基沉降量。其中桩身压缩沉降Se即为桩基沉降量S1与桩端以下土层沉降量Sb之差。
5 应用实例
根据温州大学新校区信息行政中心工程项目提供的的地质资料①,桩端以下各土层修正剑桥模型参数见表1,各土层固结试验常规分层e-p参数见表2。

表1 桩端以下各土层修正剑桥模型参数

表2 各土层固结试验常规分层e-p参数
将上述参数代入模型中,可计算出各级加载下桩基的沉降值,然后再将模型计算值与实测沉降值对比分析,结果如图5所示。由图5可知,利用本模型分析计算出的荷载—沉降关系曲线与实测曲线比较吻合,但模型计算值比实测沉降值差异略大。

图5 桩顶沉降的模型计算值与实测沉降值对比分析
桩身压缩沉降和桩端以下土层沉降量如图6所示。由图6可知,当桩顶荷载不大时,桩身压缩沉降要大于桩端以下土层沉降;当桩顶荷载持续增大到一定程度时,桩端以下土层的沉降量急剧增加,并逐渐超过桩身压缩沉降量。这主要是因为计算土层中附加应力增加,使得土层的变形逐渐由弹性变形向弹塑性变形过渡,变形量增速加快;而桩身混凝土由于其弹性模量很大,桩身变形还依然处于弹性阶段,变形增长稳定。
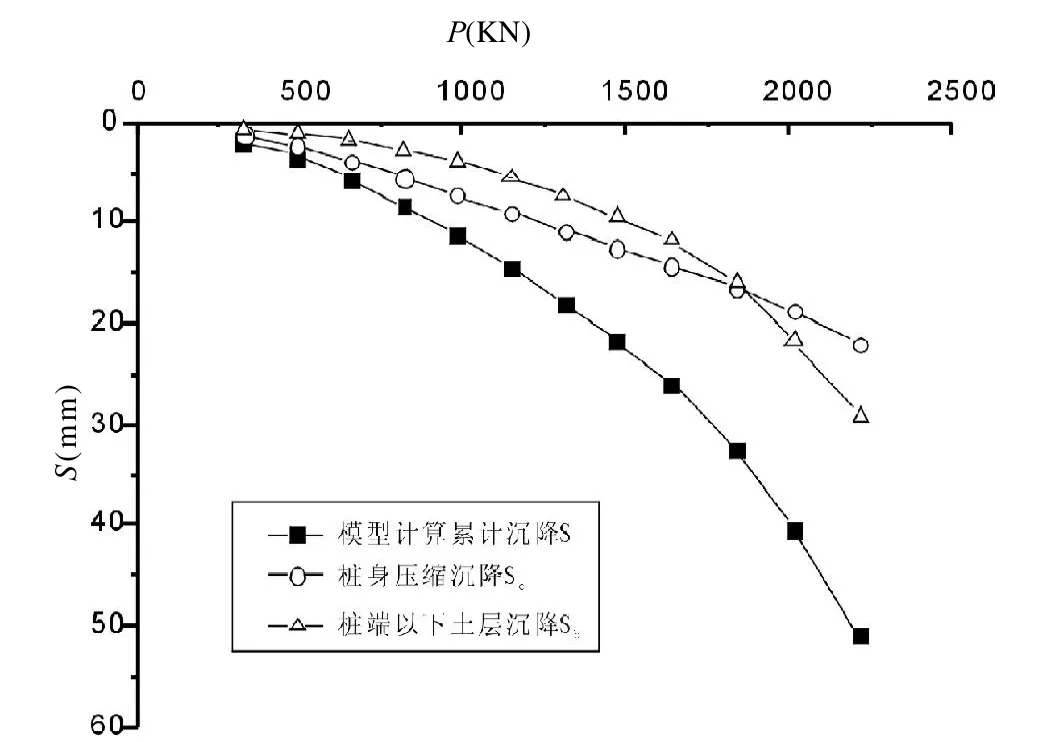
图6 试桩-1模型计算沉降组成对比分析
6 结束语
带肋填砂管桩与普通预应力混凝土管桩相比既有相似的地方也有不同的地方,且桩基沉降计算方法也不一样。基于弹塑性理论带肋填砂管桩沉降计算方法,既考虑桩身轴力较大产生的压缩沉降,又考虑桩端以下土层在较大附加应力作用下的弹塑性变形,通过修正剑桥模型函数,可判断出在附加应力作用下土层是处于弹性阶段还是弹塑性阶段,并分别加以区别计算。从实测结果比较看,计算结果与试验具有较高的吻合度,对带肋填砂管桩的应用具有一定的借鉴意义。
[1]金国平,黄敏,邹宗煊,等.扩大头带肋填砂预应力管桩的研究与应用[J].建筑结构,2006(S1):57-61.
[2]黄敏,龚晓南.一种带翼板预应力管桩及其性能初步研究[J].土木工程学报,2005(5):59-62.
[3]黄敏,龚晓南.带翼板预应力管桩承载性能的模拟分析[J].土木工程学报,2005(2):102-105.
[4]Geddes J D.Stresses in foundation soils due to vertical subsurface load[J].Geotechnique,1966(16):231-255.
[5]中华人民共和国建设部.GB 50007—2002建筑地基基础设计规范[S].北京:中国建筑工业出版社,2002:140-143.
[6]杨敏,王树娟,王伯钧,等.使用Geddes应力系数公式求解单桩沉降的讨论[J].同济大学学报:自然科学版,1997(3):71-74.
[7]何思明.基于荷载传递函数法的单桩沉降计算[J].四川建筑科学研究,1995(2):44-45,63.
[责任编辑:黄淑森]
Study and Application on Bearing Capacity of Ribbed and Sand-filled Tube Pile Based on Elastic-plastic Theory
DAI Qingbin
(Logistics Basic Construction Section, Wenzhou Vocational & Technical College, Wenzhou, 325035, China)
Ribbed and sand-filled tube pile is a new applied tube pile after the improvement of the general prestressed concrete pile. The settlement calculation of ribbed and sand-filled tube pile based on elastic-plastic theory not only takes into account of the compression settlement under the load transfer of the pile, but also the soil elastic and plastic settlement below the pile tip, and the method of coefficients between resistances of the pile tip and the pile side is presented. According to the result, the relevant statistics and their principle can be studied. Results indicates that the calculation agrees well with the measurement, and is of practical value.
Ribbed and sand-filled tube pile; Bearing capacity; Settlement; Side resistance; Elastic and plastic theory
TU473.1+1
A
1671-4326(2012)03-0049-04
2012-04-17
戴庆斌(1976—),男,安徽和县人,温州职业技术学院后勤基建处,讲师,工程师.
