矩形布局的启发式优化策略

张鹏程，王春艳，茹江燕

（1.河北工程技术高等专科学校 电力工程系，河北 沧州 061001；2.沧州设备安装技工学校，河北 沧州 061000）

矩形布局的启发式优化策略

张鹏程1，王春艳2，茹江燕2

（1.河北工程技术高等专科学校 电力工程系，河北 沧州 061001；2.沧州设备安装技工学校，河北 沧州 061000）

利用可行域算法求解矩形布局问题，通过调整矩形布入形态，改变其单一的可行域形式增大其解空间。算例结果表明，矩形调整对布局结果影响有规律，利用可行域算法求解矩形布局问题，简便、快捷、灵活、适应性强，从而能够灵活快速地获得更优异的矩形布局排布方案指导工程实践。

矩形布局；可行域；启发式算法；矩形形态；空间利用率

0 引 言

矩形布局问题作为一个具有NP-hard的组合最优化问题，广泛存在于板材切割、排样、大规模集成电路设计、服装裁剪和印刷排版等领域。由于在有限时间内无法获得全局最优解，许多学者提出各种启发式算法[1-3]用于解决不同领域的矩形布局问题，但很难找到一种对于各种不同特点的布局问题都有很好适应性的求解方法。通过对不同算例计算结果进行分析和比较得出，利用可行域算法求解矩形布局问题，简便、快捷、灵活、适应性强。

1 矩形布局问题的描述

矩形布局问题作为一类二维布局问题，将矩形作为排布对象，或利用矩形替代任意多边形或不规则图形进行排布，其特点是既保留了布局问题的复杂性，又使得问题求解一定程度上得到简化，工程实践中，有相当一部分多边形布局问题的求解是利用包络矩形将多边形转化为矩形来处理的。矩形布局问题是在给定的矩形板材上排放所需要的矩形零件，使排放区域或整张板材的废料尽可能减少，节省板材，即：给定n个矩形零件Rl，R2，…，Rn，将零件全部排放板材P上，使得板材利用率高，且满足下列约束条件：（1）对任意两个零件Ri，Rj不发生重叠，即Ri∩Rj=Φ，1≤i，j≤n且i≠j；（2）Ri必须在板材边界内，即，1≤i≤n；（3）满足一定的工艺条件。其求解目标可表述为：求最优排放序列I*，使，其中，Li为矩形的长，Wi为矩形的宽，为所有排入的矩形件的面积总和；M为所有矩形件排放完毕后所占用的板材面积。

2 利用可行域算法求解矩形布局问题

利用可行域算法求解矩形布局问题是一种很好的思路[4-6]。首先，求得每一个待布矩形在布局空间中的可行域；然后，根据定位策略,最终确定矩形最佳的摆放位置，如图1所示。单纯采用可行域算法求解矩形布局问题，根据约束条件设置定位函数参数，即可以获得较好的布局方案和较优的空间利用率。

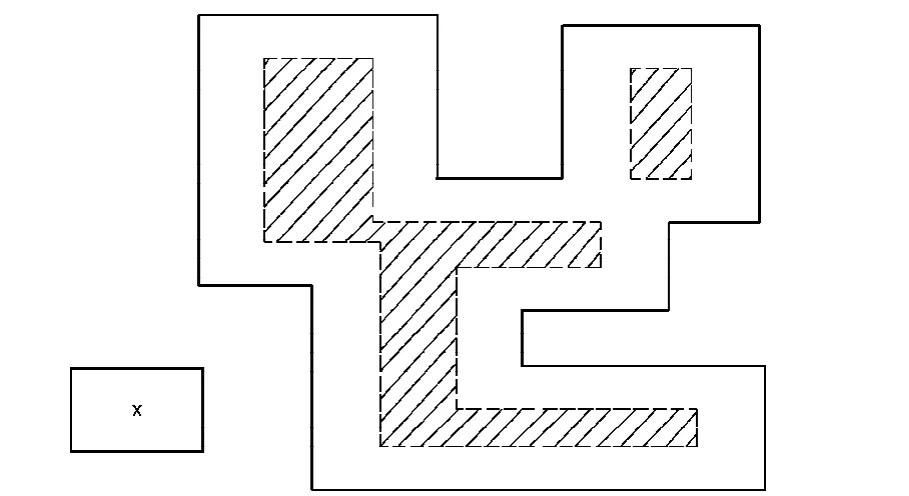
图1 矩形及其可行域

矩形可行域本质上属于矩形在其当空布局空间中的不适合多边形（NFP）。为求解过程的简化和概念的一致性，规定矩形按其原始形态进行计算，即布入时不发生旋转，而最终矩形放入布局空间的形态，由其最初输入时的状态确定。一般情况下，矩形放置方式不同，其在布局空间中的可行域大小和形态也不同（当其为正方形时例外），改变其中任一矩形的放置方式，都将会对最终布局结果产生影响。启发式布局算法对于布局问题求解的效果是以最终的布局空间占有率来衡量的，即最大程度地提高材料利用率，减少材料浪费，从而增加企业经济效益。布局问题也属于NPC问题，采用穷举法列出并比较所有布局方案的优劣是最简单、直观的策略，然而，这种方法只有当矩形数量较少的时候有效；当布局矩形达到一定规模时无疑会产生组合爆炸，而且这些计算在有限的时间内是不可能完成的。基于启发式的布局算法以人的认知经验为导向，由于个人的思维方式及研究问题的思路和出发点不同而不可避免地加入更多人为因素，故使得现有求解方法都不同程度地带有个人色彩。启发式算法虽然可以从根本上降低问题求解的复杂度维数，将问题由不可求转变为可求，并且可以在较短时间内获得较为合理的求解方案，但这些是以牺牲部分解空间为代价的。利用启发式算法只能以一定概率的方式获得最优解，或者是问题的近优解或次优解，对于工业生产中的实际问题其精确度已经足够。

3 矩形布局的启发式算法的实现

在确定矩形布入次序时，可以其面积为依据按从大到小顺序依次进行布局操作，规定已经布入布局空间的矩形位置不再发生变化，而矩形布入后布局空间会随之发生相应更新，以便为下一个矩形的放置做好准备。而先排放面积大的矩形，最后用较小的矩形填充空隙，也使得大矩形获得优先排放机会，小矩形的放置又相对灵活多变，从而尽可能提高布局空间总体的利用率。

在布局过程中，矩形放置方式(横放/纵放)不同，其可行域也不同，从而最终的布局结果也不一样。如图2所示，对于相同矩形布局空间，同一矩形横放时,可行域为900（30×30）；而纵放时，可行域为500（50 ×10）。显然，不同放置方式对后序布入的所有矩形及最终布局结果会产生很大影响，而这种影响必然从矩形布局的空间利用率表现出来。对于一个规模为N矩形布局问题（即矩形的数量为N）而言，当改变矩形的布入形态，其可能选择的布局方案比单一方式摆放方案多出2N-1种，这将大大增加布局解空间，从而使得更优秀方案的出现成为可能。

图2 矩形不同放置方式下的可行域

在矩形定位过程中，在所有有效放置位置（由矩形的可行域给出）中按照一定原则力求获得最佳放置位置，从而有利于后续矩形的布入及最终获得最优空间利用率。在定位策略的选择上，多数启法式算法的实现基于BL策略或BLF策略，本文采用文献[7]提出的定位函数法，定位函数的一般公式如下：

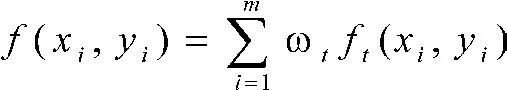
上式中，f（xi，yi）为总定位函数；ft（xi，yi）为关于各个吸引子定位函数；m为吸引子个数，吸引子原则上可以选取布局空间角上、边上、中心或任意位置；n为矩形数量；（xi，yi）为布局矩形基点坐标；（x0t，y0t）为布局吸引子坐标；αt，βt为权重因子，表示矩形摆放时出现在x轴方向或y轴方向上的概率，当αt>βt时,表示矩形优先在x方向摆放；当αt<βt时,表示矩形优先在y方向摆放。如当取吸引子的位置为布局空间左下角，矩形以相同概率摆放在x轴方向或y轴方向上时，定位函数的具体形式为：

为便于比较和计算，统一选取吸引子的位置为布局坐标系的原点，即布局空间的左下角，矩形布局测试数据集见表1。

3.1 利用可行域算法求解矩形布局

利用可行域算法对表1中所有矩形布局测试数据进行计算。求解过程中，采用矩形原始形态布入（即按strip3.xls文件中给出的长宽数据）。可行域算法测试7类共35组矩形布局测试数据的布局结果见表2。

布局结果表明，利用可行域算法可以快速有效地求解矩形布局问题，在极短的时间内获得较为理想的布局方案。随着矩形数量的增加，布局材料的空间利用率呈现上升趋势。这是因为对于相同大小的板材，当矩形数量较少时，则每一个矩形所占空间的权重就相对较大，而当每一个矩形的面积相对布局空间的比例较大时，其可行域就会相应变小，任意一个矩形不能布入，都会对最终空间占有率产生较大影响；当矩形数量较多时，矩形相对面积较小，一个矩形的布入与否不会对最终空间占有率产生较大影响，而且小矩形布局时容易“见缝插针”，布局过程更加灵活，所以最终空间利用率较高。利用可行域算法求解矩形布局问题，随着矩形数量的增加，布局效果越好，且不同矩形数据的空间利用率值越稳定，如图3所示。

表1 矩形布局测试数据集

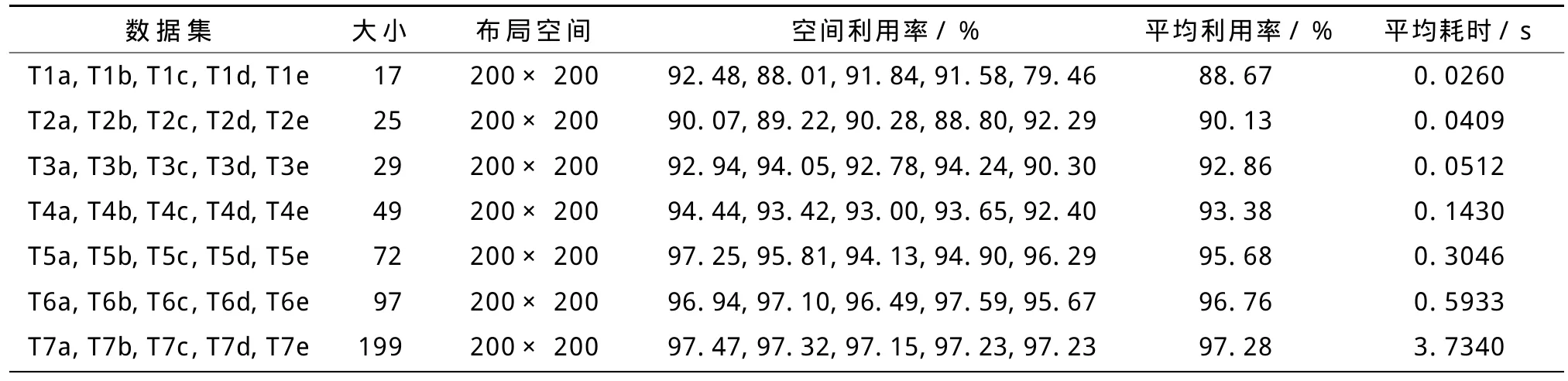
表2 可行域算法测试7类共35组矩形布局测试数据的布局结果

当无法获得布局最优解时（矩形全部布入，空间占有率100%），一定会产生有的矩形无法布入的情况。矩形无法布入的原因可能是由于布局空间本身太小，无法容纳该矩形，或者由于启发式布局策略自身的局限性所引起的，如矩形的放置位置和放置方式，不同的放置位置和放置方式一定会对后续所有矩形的放置产生影响。

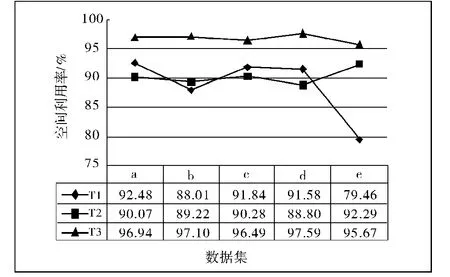
图3 T1,T2,T3三类数据布局结果比较

3.2 单一矩形旋转

矩形布局的启发式算法一般是将每一个矩形逐次放入布局空间。首先，按照布局规则和布局策略要求正确放入一个矩形，矩形放入后其位置不再发生变动，相关算法会计算布局空间所发生的变化，从而对布局空间进行更新，为下一个矩形的布入做好准备。在选定待布矩形后，确定矩形的放置方式：矩形放置方式不同，对后续矩形排布造成的影响也不一样，最终导致不同的布局结果。对于不同矩形进行旋转，取旋转后的布局结果与未旋转之前的布局结果进行比较，选取其中空间利用率较高的布局方案记录下来，将空间利用率较低的布局方案舍去。依次计算和比较每个矩形的情况，最后将空间利用率最高的结果作为最终布局方案。

以图3中直接布局结果最差的T1e组矩形布局测试数据为例，矩形数量为17个，布局空间为200×200，对T1e组矩形布局测试数据进行布局，布局结果见表3。先对所有矩形按面积降序排列，然后在布局过程中从大到小依次调整单个矩形的放置方式，获得单一矩形旋转后的布局结果见表4。单一矩形调整后的空间利用率与原空间利用率比较如图4所示。

表3 T1e组矩形布局测试数据的布局结果

从以上数据分析可以得出，通过对单一矩形布入形态进行调整，获得了更好的布局结果，空间利用率从79.46%增长为85.8125%，直接提高近7个百分点。另外，就布局矩形而言，面积较大的矩形形态的改变对最终布局结果的影响更明显，所以在设计矩形布局优化算法时，应以改变大面积的矩形放置方式为主。

3.3 多个矩形旋转

对照矩形输入时的宽度值和高度值定义的初始状态，随机调换部分矩形的宽度和高度值即改变其放置方式，从而影响最终的布局结果，增大解空间范围，通过比较从中优选出最佳布局方案。以系统时间作为种子，利用函数srand[(unsigned)time(NULL)]初始化随机数发生器，利用函数rand()产生随机数，并用算式rand()%n生成布局过程中随机发生旋转的矩形序号，n是参与布局的矩形数。从矩形旋转后产生的样本空间中随机选取1000个样本点，找到其中最优解，T1e组矩形布局测试数据多个矩形旋转后的布局结果见表5。

布局结果表明，多个矩形同时发生旋转可以进一步增大解空间，同时会有更优解出现。与表4相比，多个矩形调整放置方式比单一矩形旋转更容易获得优化布局结果，当发生旋转的矩形数量接近总数一半时，出现局部最优解的可能性较大。T1e组无矩形调整和多矩形调整方式产生的不同布局结果的比较如图5所示。

表4 T1e组矩形布局测试数据单一矩形旋转后的布局结果

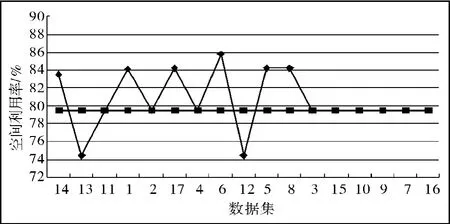
图4 单一矩形调整前后的空间利用率比较

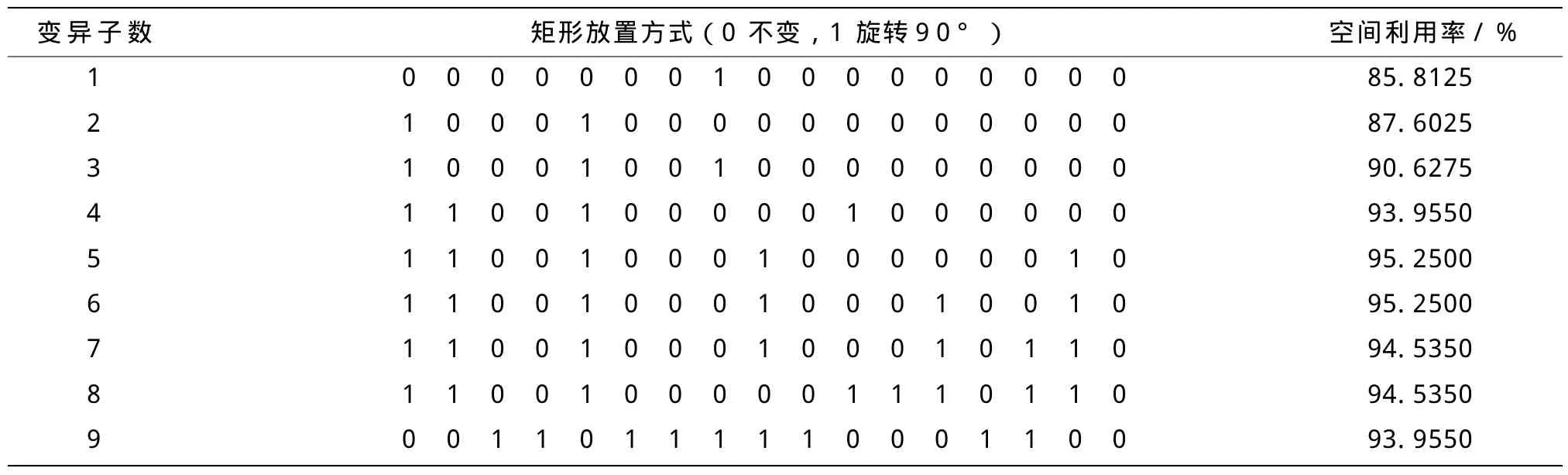
表5 T1e组矩形布局测试数据多个矩形旋转后的布局结果

4 结 论

利用可行域算法求解矩形布局问题是一种行之有效的方法，其简便、快捷、灵活、适应性强，求解结果不过度依赖矩形形式和问题规模，可以用于各种二维布局问题的求解实践中。本文在基于矩形可行域算法的基础上，引入启发式布局策略，以调整矩形布入形态特征增大解空间范围，最终通过对矩形布局过程和布局结果进行优化和优选，获得最佳矩形布局排布方案。对大量算例计算结果进行分析和比较，得出调整矩形布入形态对布局结果的影响规律，即一般情况下，多矩形调整效果优于单一矩形调整效果；而为获得更优异的布局结果，调整矩形的数量以接近矩形总数一半时为宜。

图5 T1e组矩形布局结果的比较

[1]王小港，姚林声，甘骏人.一种有效的VLSI布图规划算法[J].微处理机，2002(1):4-7.

[2] Chan H H，Markov I L.Practical slicing and non-slicing block-packing without simulated annealing[G]//ACM Special Interest Group on Design Automation.GLSVLSI’04.Boston:ACM Press，2004:282-287.

[3]Wu Y L，Huang Wenqi，LAU S，et al.An effective quasi-human based heuristic for solving the rectangle packing problem[J]. European Journal of Operational Research，2002(141):341-358.

[4]王金敏，张鹏程，朱艳华.矩形布局可行域的确定[J].计算机辅助设计与图形学学报，2008(2):246-252.

[5]张鹏程，郗艳梅，李国顺，等.利用可行域的矩形布局求解方法[J].现代制造工程，2010(3):90-93.

[6]张鹏程，郗艳梅，任红霞.矩形布局空间的处理及优化研究[J].温州职业技术学院学报，2011(1):54-58.

[7]王金敏，杨维嘉.动态吸引子在布局求解中的应用[J].计算机辅助设计与图形学学报，2005(8):1725-1730.

[责任编辑：王玮明]

Optimization for Rectangle Packing Problem Based on Heuristic Strategy

ZHANG Pengcheng1, WANG Chunyan2, RU Jiangyan2
(1. Department of Electrical Engineering , Hebei Engineering and Technical College, Cangzhou, 061001, China; 2. Cangzhou Technical School of Equipment Installation, Cangzhou, 061000, China)

In order to solve the rectangle packing problem on the basis of feasible region algorithm, the rectangle pose can be adjusted to change its single feasible region form and expand its space. The result of the numerical example shows that the impact of rectangle pose adjustment to packing problem is regular. Applying the feasible region algorithm to solve rectangle packing problem is simple, fast, flexible and adaptable, and thus a better rectangle packing problem can be obtained to guide the practice.

Rectangle packing problem; Feasible region; Heuristic strategy; Rectangle pose; Space utilization ratio

TP301.6

A

1671-4326(2012)03-0045-04

2012-03-26

张鹏程（1976—），男，河北泊头人，河北工程技术高等专科学校电力工程系，实验师，硕士；王春艳（1977—），女，河北黄骅人，沧州设备安装技工学校讲师；茹江燕（1979—），女，河北宣化人，沧州设备安装技工学校讲师.