L－相对乘积空间与θ－连通性＊

姜金平，王小霞

（延安大学数学与计算机科学学院，陕西延安 716000）

L－相对乘积空间与θ－连通性＊

姜金平，王小霞

（延安大学数学与计算机科学学院，陕西延安 716000）

借助广义Zadeh函数引入了相对乘积空间的概念，讨论了L－拓扑空间的相对乘积空间的θ－连通性，证明了θ－连通性关于这种相对乘积运算是可乘性质，即相对乘积空间是θ－连通的当且仅当其每一个因子空间都是θ－连通的．

L－拓扑空间；L－相对乘积空间；θ－连通性

文献［1］研究了广义Zadeh函数，文献［2］借助这种广义Zadeh函数引入了相对乘积空间的概念，并在其中讨论了连通性的可乘性问题．笔者在文献［3］的基础上进一步讨论了L－拓扑空间的相对乘积空间的θ－连通性，证明了θ－连通性关于这种积运算是可乘性质．

文中，LX表示非空分明集X上的L－fuzzy集的全体，LX中的最大元与最小元分别记作1和0．设δ为LX上L－fuzzy拓扑，将（LX，δ）称为L－拓扑空间，简记为L－ts．文中未定义的概念与符号均见文献［4］．定义1［1］设L1和L2是2个F格，X与Y是2个非空分明集，p：X→Y是分明映射，q：L1→L2是序同态，由p，q按下列方式诱导出一个从到的函数

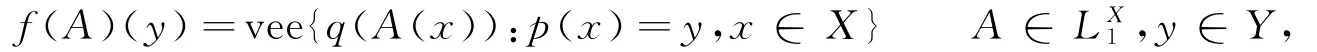
称为广义Zadeh型函数，简称GZF，记作f＝pq．

定义2［2］设是一族L－拓扑空间是投影映射，对于给定的F格L及从L到Lt的一一满序同态qt，由pt，qt诱导出来的广义Zadeh型函数称为投影序同态，则LX上以γ＝｛f－1（At）｜At∈δt，t∈T｝为子基所生成的LF拓扑δ叫做各LF拓扑空间相对于｛L，qt：t∈T｝的乘积LF拓扑空间，简称相对积空间叫做（LX，δ）的因子空间．

定义3［3］设（LX，δ）是L－fts，A∈LX，xλ∈M＊（LX），称xλ为A的θ－附着点，若对xλ的每个正则开远域U，都有A≤／U，A的所有θ－附着点之族记为A＊．称A＊之并为A的θ－闭包，记为，即A＊．A的补集的θ－闭包的补集称为A的θ－内部，记为o－，．若则称A为θ－闭集，θ－闭集的补集称为θ－开集．显然，A为θ－开集当且仅当

（ⅰ）f称为连续的，若∀A∈ε，有f－1（A）∈δ；

（ⅱ）f称为开的，若∀B∈δ，f（B）∈ε．由定义2，可知下面命题成立：

命题1［2］设（LX，δ）是的相对积空间，则每个投影序同态都是连续序同态．

定理1［5］若连续，则f一定θ－连续；反之则不一定成立．

由定理1可知：

命题2 同胚则必定θ－同胚，θ－同胚不一定同胚．

定义6［3］设（LX，δ）是L－ts，A，B，C∈LX，若，则称A与B是θ－隔离的；若存在异于0的θ－隔离集A，B，使C＝A∨B，则C称为（LX，δ）中的θ－不连通子集；若最大LF集1为θ－不连通的，则称（LX，δ）为θ－不连通空间，否则称（LX，δ）是θ－连通的．

命题3［2］设（LX，δ）是的相对乘积空间是投影序同态，则β＝｛∧t∈SPt－1（At）：S∈2（T），∀t∈S，At∈δt｝是δ的基，从而（LX，δ）中的每个闭集都可表示为形如∨t∈SPt－1（Bt）的闭集之交，这里S∈2（T），∀t∈S，Bt∈δ′t．

定义7［2］设（LX，δ）是L－ts，λ∈L，用［λ］表示X上取常值λ的LF集，若∀λ∈L，［λ］∈δ，则称（LX，δ）为满层空间．

定理2 设（LX，δ）是L－ts，A是（LX，δ）中的θ－连通集是任是θ－连续序同态，则f（A）是（）中的θ－连通集．

证明 必要性．设（LX，δ）是θ－连通空间，由命题1、定理1知是θ－连续序同态，则由定理2可得是θ－连通的．

充分性．设∀t∈T，（LXt，δt）是θ－连通的，在X中任取一点x＝｛xt｝t∈T，则由文献［2］中定理1知，过x且平行于的LF平面同胚，由命题2知－同胚，从而是（LX，δ）中的θ－连通子集，它显然包含点x1．以C记（LX，δ）中包含点x1的θ－连通分支，设y＝｛yt｝t∈T是X中仅有第s个坐标ys与xs不相同的任一点，则y1与x1同属于从而y1≤ C，即（LX，δ）中承点仅差1个坐标的2点是包含于同一个θ－连通分支之中的，因此承点相差有限多个坐标的点也是包含于同一个θ－连通分支之中的．特别地，若Z＝｛zt｝t∈T与x只有有限个坐标不同，则z1≤C．

令B＝∨｛uλ｜u＝｛ut｝t∈T与x仅有有限多个坐标不同，λ∈M（L）｝，则由以上证明知B≤C．下证B－θ＝1．

先证B是分明集．设uλ∈B，则∀μ∈M（L），uμ∈B，这一点由B的定义可得出，由于∨M（L）＝1，u1＝∨｛uλ｜λ∈M（L）｝≤B，所以B是分明集．

则R（z）＝R（ω）≠0．

［1］ HE Wei．Generalized Zadeh Function［J］．Fuzzy Set and Systems，1998，97：381－386．

［2］ 李进金．LF拓扑空间的相对乘积空间与连通性［J］．苏州大学学报，2002，18（2）：4－7．

［3］ 姜金平，马保国，王小霞．LF－拓扑空间的θ－连通性［J］．纺织高校基础科学学报，2004，17（3）：190－193．

［4］ 王国俊．LF拓扑空间论［M］．西安：陕西师大出版社，1988．

［5］ 杨建新．L－fuzzyθ－良紧空间［J］．模糊系统与数学，2000（2）：30－37．

Relative Productive Spaces in L－Topological Spaces andθ－Connectedness

JIANG Jin－ping，WANG Xiao－xia
（College of Mathematics and Computer Science，Yan’an University，Yan’an 716000，Shaanxi China）

The relative product spaces are introduced by the generalized Zadeh function and theθ－connectedness is discussed in the relative product spaces of L－topological spaces．The product ofθ－connectedness to the relative product spaces is proved．That is，the relative product spaces areθ－connected if and only if each factor space isθ－connectedness．

L－topological space；relative product spaces；θ－connectedness

O189．1

A

10．3969／j．issn．1007－2985．2012．02．003

（责任编辑 向阳洁）

1007－2985（2012）02－0010－03

2011－11－12

国家自然科学基金资助项目（10871156）；陕西省教育厅科研项目（08JK498）

姜金平（1974－），男，陕西洛川人，延安大学学数学与计算机科学学院副教授，博士，硕导，主要从事科学计

算与格上拓扑学研究．