余模的AuslanderReiten平移＊－

祝家贵，黎奇升，魏丽娟

（1．巢湖学院数学系，安徽合肥 238000；2．吉首大学数学与计算机科学学院，湖南吉首 416000；3．湖南理工学院数学学院，湖南岳阳 414000）

余模的AuslanderReiten平移＊
－

祝家贵1，黎奇升2，魏丽娟3

（1．巢湖学院数学系，安徽合肥 238000；2．吉首大学数学与计算机科学学院，湖南吉首 416000；3．湖南理工学院数学学院，湖南岳阳 414000）

设Γ是域k上的余代数，对函子作进一步研究，其中表示MΓ中由拟有限余表示余模确定的完全子范畴．证明了当Γ是半完备余代数时，τ是范畴与之间的等价，其中是内射（投射）稳定范畴是中有限维射内射（投射）余模作成的完全子范畴．

余代数；余模；转置；平移

1 问题的提出

设Γ是域k上的一个余代数，MΓ表示右－Γ余模范畴，对于M ∈MΓ，如果对每个有限维F∈MΓ有 dimkComΓ（F，M）＜＋∞，那么称M是拟有限的，用表示MΓ中由拟有限余模确定的完全子范畴．对于M∈MΓ，如果M的极小内射余表示0→M→I0→I1满足Ii是拟有限内射余模（i＝0，1），那么称M是拟有限余表示的，用表示MΓ中由拟有限余表示余模确定的完全子范畴．如果M的极小投射表示满足Pi是拟有限的投射余模（i＝0，1），那么称M是拟有限表示的，用表示MΓ中由拟有限表示余模确定的完全子范畴．文献［1］中引进了一个函子，其中Γop表示Γ的反余代数，如果既不可分解又不是内射的且dimkTrM＜＋∞，证明了在范畴MΓ中几乎分裂序列0→M→E→DTrM→0的存在性，其中D＝Homk（，k）；如果Γ是右半完备余代数，且对每个单模S∈MΓ，dimk（Soc（I（S）／S））＜＋∞，其中I（S）是S的内射包，Soc是基座，那么对每个有限维M∈MΓ，以上几乎分裂序列存在且dimkDTrM＜＋∞．笔者对函子Tr及τ＝DTr作进一步研究，简化了文献［1］关于函子Tr的引进方法，证明了函子τ是范畴与之间的等价，其中是内射（投射）稳定范畴是中有限维射内射（投射）余模作成的完全子范畴．为方便起见，用Inj MΓ（PMΓ）表示MΓ中所有内射（投射）余模作成的类．

2 转置函子Tr

如果M，N∈MΓ，那么记M到N的右Γ－余模同态全体为ComΓ（M，N）．现需要Hom函子的对偶概念，Cohom函子hΓ（，），它是右正合加法函子［2］．

引理1［3］设，那么M 是不可分解内射的充要条件是存在一个本原幂等元e ∈Γ＊＝Homk（Γ，k），使得M≅Γe作为右Γ－余模同构．

事实上，如果I∈MΓ是不可分解内射余模，那么由引理1，存在本原幂等元e∈Γ＊使得I≅Γe，这时It＝hΓ（I，Γ）≅hΓ（Γe，Γ）≅eΓ．由于eΓ是Γ作为右Γop－余模的直和项，从而eΓ是拟有限内射的Γop－余模．对于一般情况，只需利用函子（－）t的可加性．

记TrM＝Ker ft，称为M的转置（transpose）．现在有一个右Γop－余模正合列：

由于内射包，继而极小内射余表示在同构意义下是唯一确定的，因此右Γop－余模TrM 在同构意义下是唯一的．

转置函子Tr的主要性质归纳如下（参考文献［1］中的命题3．2）．

（ⅰ）右Γop－余模TrM没有非0的内射直和项；

（ⅲ）M是内射的充要条件是TrM＝0，如果M不是内射的，那么TrM是不可分解的且Tr（TrM）≅M；

其中u：E1′→E0′是右Γop－余模同态．用（－）t函子作用，得到M以下形式的内射余表示：

这与M 内射余表示的极小性矛盾．

应用函子（－）t到（ⅱ）中的正合列，可以得到行正合的交换图：

事实上，假定同态w存在，考虑以下交换图：

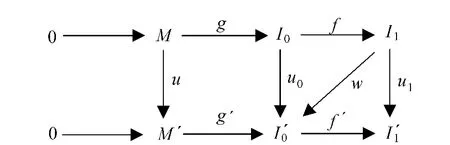
因为f′（u0－wf）＝0，所以Im（u0－wf）⊆Ker f′＝Img′，于是存在v：I0→M′使得g′v＝u0－wf，但g′vg＝（u0－wf）g＝u0g＝g′u，从而vg＝u（g′是单同态），因此u∈I（M，M′），从而F（u0，u1）＝0．反过来，如果F（u0，u1）＝0，那么由u0，u1诱导的同态u通过内射余模分解．因为g是一个单同态，从而存在v：I0→M′使得u＝vg．现在（u0－g′v）g＝u0g－g′vg＝u0g－g′u＝0，由此推出存在一个同态使得wf＝u0－g′v．因此f′wf＝f′（u0－g′v）＝f′u0．

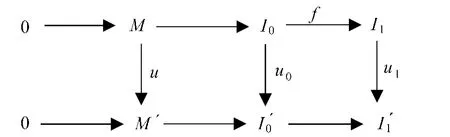
还有一个“行正合”的图：

应用函子（－）t得到以下交换图：

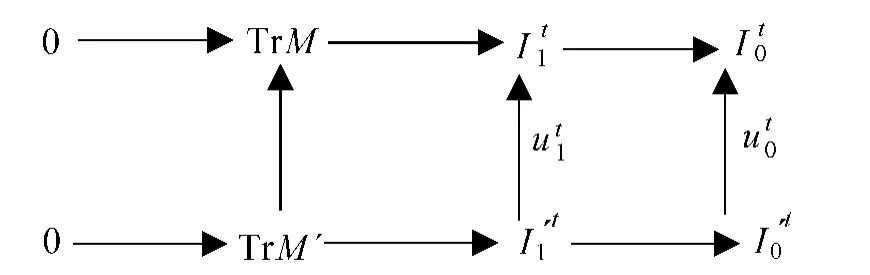
令Tru：TrM′→TrM是使得以上左方块图交换的唯一的同态，由此推出是一个对偶函子．

3 Auslander－Reiten平移

转置Tr将右Γ－余模变成右Γop－余模，现希望在右Γ－余模范畴

内构造一个范畴等价，这需要与标准对偶函子D＝Homk（－，k）合成．

关于标准对偶D＝Homk（－，k）在有限维余模范畴中的基求性质，有类似文献［5］中定理5．13的的结论，读者可以直接给出证明．

引理2 设Γ是一个余代数，D＝Homk（－，k）：f．d．MΓ→f．d．MΓop是标准对偶，那么以下结论成立：

（1）0→L→uN→hM→0在f．d．MΓ中是正合的在f．d．MΓop中是正合的．

（2）设E，P∈f．d．MΓ，那么E∈Inj MΓ⇔D（E）∈PMΓop，P∈PMΓ⇔D（P）∈Inj MΓop．

（3）余模S∈f．d．MΓ是单的⇔D（S）∈f．d．MΓop是单的．

（4）单同态u：M→E是f．d．MΓ中的一个内射包⇔满同态D（u）：D（E）→D（M）是f．d．MΓop中的一个投射盖；满同态h：P→M是f．d．MΓ中的一个投射盖⇔单同态D（h）：D（M）→D（P）是f．d．MΓop中的一个内射包．

定义1 令τ＝DTr和τ－1＝TrD，称τ为Auslander－Reiten平移．称为Nakayama函子．

（ⅱ）由M的极小投射分解P1→P0→M→0，用D去作用，得到DM的极小内射分解0→DM→DP0→DP1．再用（－）t＝hΓ（－，Γ）去作用，有0→Tr（DM）→（DP1）t→（DP0）t→（DM）t→0．由于对每个M∈MΓ，（DM）t＝hΓ（DM，Γ）≅hΓ（DΓ，DDM）≅hΓ（DΓ，M）≅υ－1M，因此以上同构诱导以下正合列：

由这个命题可以立即给出一个余模其内射（投射）维数至多是1的判定方法．

证明 （ⅰ）由命题1（ⅰ），用右正合函子υ－1＝hΓ（DΓ，－）作用到正合列→0，得到行正合的交换图：

因此υ－1τM＝hΓ（DΓ，τM）≅Coker f＝0⇔inj．dim（M）≤1．

（ⅱ）由命题1（ⅱ），用υ＝DhΓ（－，Γ）去作用正合列，得到以下交换图：

因此υ（τ－1M）＝DhΓ（τ－1M，Γ）≅Ker f＝0⇔pro．dim（M）≤1．

（ⅰ）余模τM＝0⇔M是内射余模；

（ⅱ）余模τ－1N＝0⇔N是投射余模；

（ⅲ）如果M不是内射余模，那么τM是不可分解的非投射余模，且τ－1τM ≅M；

（ⅳ）如果N不是投射余模，那么τ－1N是不可分解的非内射余模，且ττ－1N≅N；

（ⅴ）如果M和N不是内射余模，那么M≅N⇔存在同构τM≅τN；

（ⅵ）如果M和N不是投射余模，那么M≅N⇔存在同构τ－1M≅τ－1N．

证明 （ⅰ）τM＝DTrM＝0⇔TrM＝0⇔M是内射余模．

（ⅱ）τ－1M＝Tr（DM）＝0⇔DM是内射余模⇔N是投射余模．

（ⅲ）M不是内射的，那么TrM是不可分解的，从而D（TrM）＝τM是不可分解的．如果τM是投射的，那么τ－1（τM）≅M＝0，矛盾．

（ⅳ）N不是投射余模，那么DN是不可分解的、非投射的Γop－余模［4］，从而τ－1N＝TrDN是不可分解、非内射的Γ－余模．

（ⅴ）和（ⅵ）是显然的结论．

推论2 Auslander－Reiten平移τ和τ－1确定了以下范畴等价

［1］ CHIN W，KLEINER M，QUINN D．Almost Split Sequence for Comodules［J］．J．Algebra，2002，249：1－19．

［2］ TAKEUCHI M．Morita Theorems for Categories of Comodules［J］．J．Fac．Sci．Univ．Tokyo，1977，24：629－644．

［3］ CUADRA J，TORRECILLAS G J．Idemoptents and Morita－Takeuchi Theory［J］．Comm．in Algebra，2002，30（5）：2 405－2 426．

［4］ LIN I－P．Semiperfect Coalgebra［J］．J．Algebra，1977，49：357－373．

［5］ ASSEM I，SIMSON D，SKOWRONSKI A．Elements of the Representation Theory of Associative Algebras［M］／／Techniques of Representation Theory．London Mathematical Society Student Texts 65，2006．

Auslander－Reiten Translations for Comodules

ZHU Jia－gui1，LI QI－sheng2，WEI Li－juan3
（1．Department of Mathematics，Chaohu College，Hefei 238000，China；2．School of Mathematics and Computer Science，Jishou University，Jishou 416000，Hunan China；3．School of Mathematics，Hunan Institute of Science and Technology，Yueyang 414000，Hunan China）

LetΓbe a coalgebra over a field k．Further discussion of the functorτ＝DTr：is car－ried out，wheredenotes the full subcategory of MΓdetermined by the quasi－finitely copresented co－modules．IfΓis a semisimple coalgebra，it is proved that the functorτ：f．d．is a categories equivalence，whereis the injectively（projectively）stable category and f．d．is the full subcategory ofdetermined by the finite dimensional injective（projective）comodules．

coalgebra；comodule；transpose；translation

O153．3

A

10．3969／j．issn．1007－2985．2012．02．001

（责任编辑 向阳洁）

1007－2985（2012）02－0001－06

2012－01－07

湖南省教育厅重点科学研究项目（08A057）

祝家贵（1961－），男，安徽六安人，巢湖学院数学系教授，博士，主要从事同调代数、Hopf代数、代数表示论

研究；黎奇升（1964－），男，湖南桑植人，吉首大学数学与计算机科学学院教授，博士，主要从事同调代数、代数K－理

论、算子代数研究．