铁路新型钢－混凝土组合桁架桥在列车作用下的动力响应分析

郭薇薇，夏 禾，李慧乐，张 田

(北京交通大学 土木建筑工程学院，北京 100044)

钢－混凝土组合桁架(见图1)是近年来发展起来的一种新型结构，是一种由三角形桁架和混凝土槽形板组成的组合结构。在桁架结构中，腹杆采用钢箱混凝土，上、下弦杆均采用混凝土结构，因此用钢量大幅度降低，降低了工程造价。而且它的刚度较钢桁梁明显增强;与系杆拱桥相比，建筑高度可降低1.5～2.0 m。这种钢－混凝土组合桁架桥可采用拖拉法施工，简单方便，并可较少对地面道路交通的影响。此外，桥梁后期养护维修的工作量也较钢桁梁大为降低。基于上述优点，日本、法国、德国、瑞士等国家都对该桥型进行了大量研究，并已成功应用于工程实践［1］。

图1 钢－混凝土组合桁架Fig.1 Steel-concrete composite truss

国内对这种钢－混凝土组合桁架桥的研究相对较少。2005年，结合京郑黄河公铁两用桥设计方案竞标，中铁第一勘察设计院首次提出了以组合桁架作为腹板的空腹式箱梁结构主梁，对该结构进行了初步研究［2－3］。2008年11月，西安至平凉铁路开工建设。西平铁路正线全长263.1 km，为国家I级单线铁路，设计时速120 km。其中，跨越银武高速立交中的马屋泾河特大桥主桥采用了1孔80 m钢－混凝土组合桁架结构。本文通过列车－桥梁时变系统空间振动动力仿真分析，对这种新型铁路桥梁结构的动力特性及其在不同等级铁路中的适应性能进行了研究分析。

1 分析模型的建立

列车－桥梁动力相互作用空间分析模型由车辆模型、桥梁模型组合而成。将车辆与桥梁看作一个联合动力体系，以轮轨接触处为界面，分别建立两者的运动方程，通过轮轨几何相容条件和相互作用力平衡条件来联系［4－9］。

1.1 车辆模型

铁道车辆是由车厢体、转向架、轮对及弹簧－阻尼悬挂装置组成的多自由度振动系统。其在垂向平面内的运动关系，可视为多刚体系统来考虑。考虑到本文主要计算列车荷载作用下的桥梁整体振动响应，对每节机车或车辆模型，采用以下假定:

(1)车辆沿线路方向作等速运动，不考虑车体、转向架和轮对沿车辆纵轴方向的振动。

(2)相邻车辆的连接装置不影响车辆竖向及横向平面内的振动。

(3)钢轨与桥面之间无相对运动，忽略轨枕和扣件的弹性变形。

(4)车辆的一系、二系悬挂阻尼均简化为粘滞阻尼器，即阻尼力与振动速度成正比。

(5)第i节车车体考虑横摆Yci、沉浮Zci、侧滚θci、摇头Ψci和点头φci等5个自由度;第i节车第j个转向架考虑横摆 Ytij、沉浮 Ztij、侧滚 θtij、摇头 Ψtij和点头 φtij等5个自由度;第i节车第j个转向架第l个轮对考虑横摆Ywijl、沉浮Zwijl和侧滚θwijl等3个自由度。

为了更好地研究这种铁路新型钢－混凝土组合桁架桥在不同等级铁路中的适应性能，在动力分析中，桥上的列车型式包括货车、中速客车和高速客车等三种类型。对于具有二个转向架、采用二系悬挂装置的六轴机车，计算自由度为33;对于采用一系悬挂装置的四轴货车，计算自由度为17;而对于二个转向架、采用二系悬挂装置的四轴机车及客车，计算自由度为27。车辆的计算模型见图2所示。

1.2 桥梁模型

在研究车－桥系统的横向和竖向振动时，一般多采用空间有限元模型对桥梁进行分析。本文采用振型分解法，将数量庞大的桥梁各节点的耦合运动方程组转化成结构前若干阶振型的运动方程，既能保证计算精度又能大大减少计算工作量。桥梁第n阶振型的动力平衡方程可写为:

式中:qn是广义坐标，即模态振幅;ξn和ωn分别为桥梁第n阶振型的阻尼比和圆频率;Fn是广义力:

图2 车辆计算模型示意图Fig.2 Computation model of train vehicle

式中:Nv为桥上的车辆总数;Nwi是第i节车每个转向架上的轮对数;Fnijl为第i节车第j个转向架第l个轮对对桥梁产生的广义力，由三部分组成:

式中:φnh(x)、φnθ(x)和 φnv(x)分别为桥梁第n阶振型的水平、扭转和竖直分量;xijl是第i节车第j个转向架第l个轮对沿桥梁长度的位置;Fhijl、Fθijl和 Fvijl分别为第i节车通过第l个轮对作用于桥梁的水平分力、扭转分力和竖直分力，可根据该轮对的运动加速度及其与桥面结构的相对位移和速度确定:

式中:Mci、Mtij、mwijl分别是车体、转向架和轮对的质量;Jwijl为轮对的质量惯性矩;g是重力加速度;为一系悬挂横向弹簧刚度系数和阻尼系数;为一系悬挂竖向弹簧刚度系数和阻尼系数;di是轴距之半;h3i和h4i分别是从转向架中心至轮对中心、轮对中心至梁体中心的垂直距离;ai是车轮横向跨距之半，见图3。

图3 车轮与桥梁的相互作用关系Fig.3 Relationship of wheel and bridge

1.3 轮轨运动关系

多年来，对轮轨关系尤其是轮轨间接触力的研究，一直是车桥系统动力相互作用分析中的核心问题之一。轮轨关系的处理方法主要有四种:① 通过简化车轮为锥形踏面，由轮轨相互位置关系确定轮轨间的相互作用力。② 绕过轮轨相互作用，直接研究轨道和转向架构架之间的关系，而将实测转向架构架波作为车桥系统的输入。③ 利用轮轨滚动接触理论，考虑轮轨间的蠕滑作用，建立详细的轮轨相互作用模型，用解析方法研究曲线形车轮踏面与钢轨之间的相对位置关系和相互作用力。④ 根据有限区间内的轨道不平顺样本假定轮对和轨道之间的相对位移关系，以此来考虑轮轨相互作用关系。本文采用的是第④种方法，这种方法比较简单，主要特征参数来自实测数据，因而可以反映轮轨关系的主要特征，是一种常用的方法。

轨道不平顺样本的获取有两条途径:一是通过在实际线路上测试得到;一是根据不同等级铁路的轨道不平顺功率谱密度函数进行数值模拟得到。

第i节车第j个转向架第l个轮对的位移Ywijl、θwijl、Zwijl可以由桥梁振型广义坐标以及相应的轨道不平顺位移的叠加来表示:

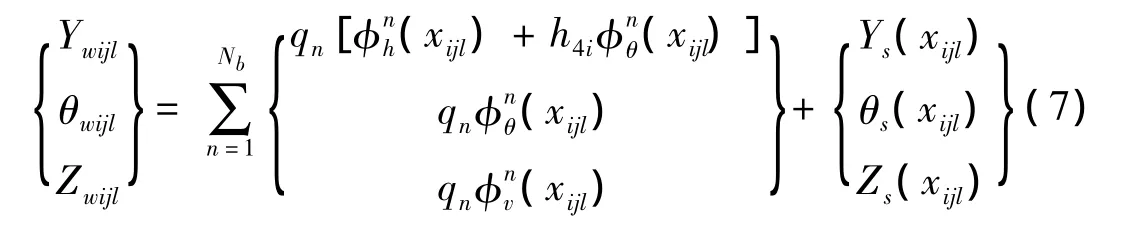
式中:Nb是计算中所采用的振型数;Ys(x)、θs(x)、Zs(x)分别是方向、水平和高低不平顺位移。

2 计算结果与分析

2.1 桥式概况

西平铁路马屋泾河特大桥主桥采用三角形桁架和混凝土槽形板相结合的组合桁架结构，见图4(a)。上弦纵杆、横联杆采用C50混凝土杆件，纵杆之间相距6.6 m。主桁桁高 10.5 m。腹杆采用 0.56 m ×0.66 m钢箱中灌注混凝土形式。混凝土槽形板宽7.7 m，中心部分板厚0.45 m。腹杆下端插入槽形板与其直接相连，上端通过节点板与上弦纵杆相连。二期恒载7.5t/m。作为动力分析的第一步，本文首先对马屋泾河特大桥主桥自振特性进行了计算分析。采用大型结构有限元分析软件Midas对该桥建立了三维空间梁单元模型，见图4(b)。模态分析结果表明，结构的一阶振型为横向正对称振动，频率为1.395 Hz;二阶振型为竖向正对称振动，频率为 2.383 Hz。

图4 马屋泾河特大桥主桥示意图Fig.4 Illustration of Mawu Jinghe Bridge

2.2 计算条件

马屋泾河特大桥为单线铁路桥，客货共线。为了研究这种铁路新型钢－混凝土组合桁架结构在不同等级铁路中的适应性能，采用自编车－桥动力分析程序对该桥进行了车桥动力仿真计算。计算中选用的列车有3种:(a)重载货车，29节编组:1节DF4机车+28节C62重载货车，计算车速40～80 km/h;(b)中速客车，19节编组:1节DF11机车+18节25T列车)，计算车速120～180 km/h;(c)高速客车，德国ICE3动力分散独立式高速列车，16节编组:(3动+1拖)×4，计算车速250～420 km/h。三种车型的轴重、轴距、车辆全长见表1。

表1 三种车型的轴重、轴距和车辆全长Tab.1 Axle load，wheel base and full length of 3-types of vehicle

表2 三种轨道不平顺样本的统计特征Tab.2 Statistical characteristics of three irregularity samples

针对上述三种车型，计算中选用的轨道不平顺数据分别为:美国5级谱生成轨道不平顺样本、郑武线实测轨道不平顺样本、德国低干扰谱生成轨道不平顺样本。三种轨道不平顺样本统计特征见表2。

选取桥梁结构前40阶振型参与车－桥耦合动力计算，涵盖频率范围为1.395～23.125 Hz。结构的阻尼比取为0.02。时间步长取为0.002 s。

2.3 车桥动力响应

图5给出了三种列车以不同的速度通过引起的桥梁跨中竖向挠度的时程曲线。该值随车速的分布情况见图6。从图中可以看出，由重载货车引起的桥梁竖向挠度响应值最大，分析原因，该值主要受列车的移动重力加载作用的控制。在所有计算工况下，桥梁最大跨中竖向挠度为9.77 mm，可推算其挠跨比约为1/8 188，远小于我国铁路现行规范所规定的限值。表明该桥型在运行列车作用下具有较大的竖向变形刚度。

此外，由运行列车引起的桥梁跨中横向位移响应值也比较小，见图7～图8。各种工况下的最大振幅约为0.23 mm，满足我国铁路规范的限值要求。表明该桥型同时具备较大的横向变形刚度。

在运行列车作用下，桥梁的竖向振动加速度响应的时程曲线见图9所示，随车速的分布情况见图10。从图中可以看出，在所有计算工况中，由重载货车引起的桥梁竖向加速度响应最大，高速客车次之，中速客车最小。该值在车速40～80 km/h范围内随车速的增大而增大，当货车车速达到80 km/h时，桥梁跨中竖向加速度的幅值为0.66 m/s2，远小于我国铁路规范规定的桥面板在20 Hz及以下强振频率作用下的竖向振动加速度的限值。

图9 桥梁跨中竖向振动加速度时程曲线Fig.9 Time history of vertical acceleration at bridge mid-span

图10 桥梁跨中竖向振动加速度随车速的变化Fig.10 Vertical acceleration of bridge mid-span vs train speed

图11是桥梁跨中横向振动加速度的时程响应曲线。从图中可见，由高速客车引起的桥梁横向加速度响应最大，中速客车次之，重载货车最小。该值随车速的变化呈起伏变化，见图12所示。在所有计算工况中，桥梁跨中横向加速度的幅值约为0.42m/s2，也远小于规范限值。可见该桥在运行列车作用下的动力性能较好，横、竖向振动加速度响应值都很小，从而避免出现过大的轮轨接触力。

三种列车在桥上的车体振动加速度时程曲线见图13。车体的振动加速度是衡量车辆运行平稳性的重要指标，也是判定桥梁竖向刚度和横向刚度能否满足要求的一个重要指标。参考我国铁路规范，各种车速下的车体最大横、竖向振动加速度的计算结果及评价见表3～表4所示。从表中可以看出，当重载货车、中速客车、高速客车以不同车速通过桥梁时，车辆的最大横、竖向振动加速度响应均能较好地满足规范要求。

列车的运行安全性可通过脱轨系数、轮重减载率、轮轴横向力等三个指标来评定。其中，脱轨系数定义为轮对一侧车轮的横向压力与动轮重之比;轮重减载率定义为减载侧车轮的轮重减载量与轮对的平均静轮重之比;轮轴横向力为一个轮对上左右两个车轮的横向力之和。这三个指标均可通过车桥动力仿真分析计算得到。我国铁路规范对其的限值要求见表5～表7。本文分别计算了三种型式列车以不同的速度通过马屋泾河大桥时，桥上车辆的最大脱轨系数、轮重减载率及轮轴横向力响应，见表5～表7。从表中可以看出，车辆的最大脱轨系数、轮重减载率、轮轴横向力响应均在规范限值之内，说明桥上车辆的运行安全性可以得到保证。

表3 车体横向振动加速度计算结果及评价Tab.3 Results and evaluations of lateral car-body acceleration

表4 车体竖向振动加速度计算结果及评价Tab.4 Results and evaluations of vertical car-body acceleration

图13 车体振动加速度时程曲线Fig.13 Time history of car-body acceleration

表5 桥上车辆脱轨安全性评价Tab.5 Evaluation of derailment factors of vehicles on bridge

表6 桥上车辆轮重减载安全性评价Tab.6 Evaluation of offloading factors of vehicles on bridge

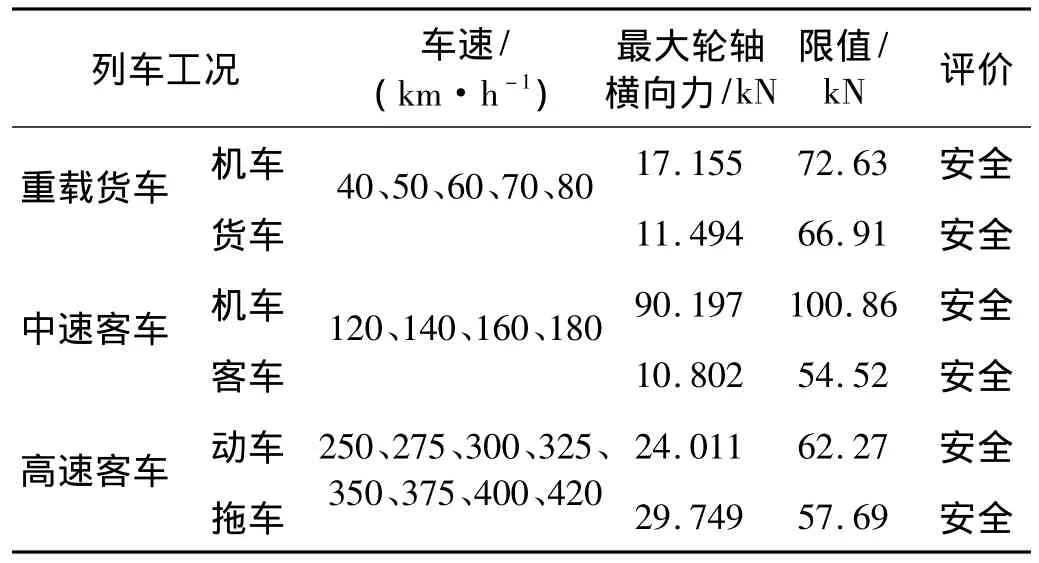
表7 桥上车辆轮轴横向力安全性评价Tab.7 Evaluation of lateral wheel/rail forces of vehicles on bridge

3 结论

本文分析了一种铁路新型钢－混凝土组合桁架桥的动力特性，对其在C62重载货车、25T中速客车以及高速客车德国ICE高速动车组以不同速度分别通过时的车桥耦合振动特性进行了数值计算，得到如下主要结论:

(1)在所有列车荷载工况下，桥梁的最大横向位移为0.23 mm，最大竖向挠跨比为1/8 188，最大横、竖向加速度分别为 0.42 m/s2、0.66 m/s2，均能较好地满足我国铁路现行规范要求。

(2)桥上车辆的脱轨系数、轮重减载率、轮轴横向力以及车体横、竖向振动加速度响应也在规范限值之内。

(3)数值计算结果表明，该铁路新型钢－混凝土组合桁架桥式方案在运行列车作用下动力性能良好，满足重载货车、中速客车及高速客车的行车要求。此外，列车在桥上的运行安全性和平稳性也可以得到保证。表明该新型钢－混凝土组合桁架桥可广泛用于我国货运、普通客运及高速铁路的桥梁设计。

［1］ 刘玉擎.组合结构桥梁的发展与展望［A］.中国公路学会桥梁和工程结构分会2005年全国桥梁学术会议论文集［C］.北京:人民交通出版社，2005，186－192.

［2］ 赵会东，李承根，吴少海.新型钢－混组合结构的发展现状及展望［J］.铁道勘察，2007，增刊:54－56.

［3］ 赵会东，蔡 正，雷潘宁.组合结构在高墩大跨梁桥中的应用研究［J］.铁道勘察，2007，增刊:42－43.

［4］ 夏 禾，张 楠.车辆与结构动力相互作用［M］.第2版.北京:科学出版社，2005.

［5］ 姚仲达，杨永斌.高速铁路车－桥互制理论［M］.台北:图文技术出版有限公司.2001.

［6］ 郭薇薇，夏 禾.直线电机列车作用下高架桥的动力响应分析［J］.中国铁道科学，2007，28(4):55－60.

［7］ Zhang N，Xia H，Guo W W.A vehicle-bridge linear interacted model and its validation［J］.International Journal of Structural Stability and Dynamics，2010，10(2):335－361.

［8］ 高芒芒.高速铁路列车－线路－桥梁耦合振动及列车走行性研究［J］.中国铁道科学，2002，23(2):135－138.

［9］ 李小珍.强士中.列车－桥梁耦合振动研究的现状和发展趋势［J］.铁道学报，2002，24(5):112－120.