基于FEM和BEM法的大型立式齿轮箱振动噪声计算及测试分析

焦映厚，孔 霞，蔡云龙，张介禄，周亚政

(1.哈尔滨工业大学 机电工程学院，哈尔滨 150001;2.江苏泰隆减速机股份有限公司，泰兴 225400)

行星齿轮传动具有较大传动比、较高效率且结构紧凑，能实现分路、换向传动，具有减速、增速、运动合成与分解等用途，适用于航空、舰船、汽车和其他机械工业。振动与噪声是影响行星齿轮传动减速器系统可靠性与寿命的关键因素，且由于同时存在外部激励与内部激励，使得行星齿轮传动减速箱的振动与噪声现象相对较为复杂。目前，对于齿轮传动的建模和数值分析，多是取齿轮传动的零部件分别进行建模和分析的［2］。本文针对某大型立式行星传动齿轮箱的结构和安装特点，首先计算该齿轮箱内部各齿轮零部件运转时产生的振动激励，再利用有限元软件ANSYS对齿轮箱进行有限元建模，计算齿轮箱的模态频率和稳态不平衡响应，然后将不平衡响应结果导入声学软件LMS Virtual lab计算其辐射声场，最后将预测结果与实测结果进行了比较。

1 立式行星齿轮传动减速箱的结构安装特点

该大型立式行星传动齿轮箱采用2K－H NGW型行星齿轮传动，太阳轮由鼓形齿联轴器连接输入，内齿圈固定，行星架输出。工作状态下，该齿轮箱竖直置放于机架上，太阳轮浮动，机架上部为输入电机，下部为输出端。额定输入功率为5 900 kW，额定输入转速为994 r/min，输出转速为180 r/min，额定输出扭矩为375 150 N·m。该齿轮箱的安置工况如图1所示。

图1 立式行星传动齿轮箱安置工况图Fig.1 Placement of vertical planetary transmission gearbox in working condition

2 立式行星齿轮传动减速箱及机架的模态分析及稳态不平衡计算

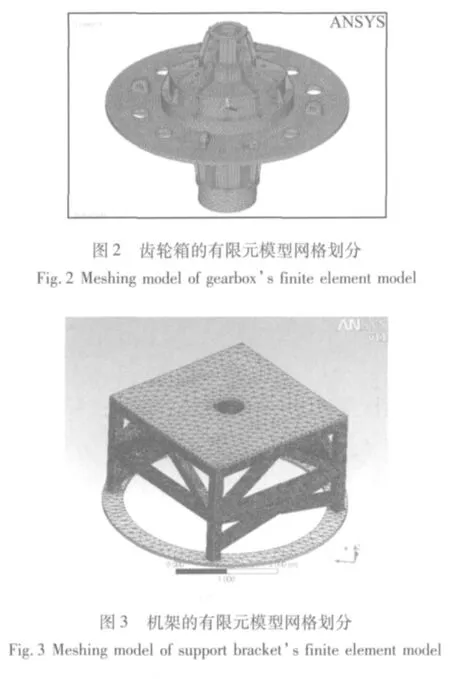
选用Block Lanczos法进行求解，该求解器采用稀疏矩阵进行求解，适用于求解如本文研究的齿轮箱这类的大型对称结构和单元规整的有限元模型，可以求解子空间法求解的任何结构，且有更快的收敛速度。

分析行星轮系径向振动响应，即是分析齿轮耦合对转子系统的不平衡响应。不平衡响应是行星齿轮转子系统在不平衡力或不平衡力矩的激励下所产生的振动，求解不平衡响应，必须已知转子不平衡量的大小及其分布规律。基于Timoshenko理论，采用Beam188二次三节点梁单元建立输入、输出轴模型，采用点单元MASS21模拟转子。采用可扭转的刚度阻尼单元Combin14模拟齿轮啮合，采用2自由度带有交叉刚度的弹簧阻尼单元combin214来模拟轴承。对于本系统来说，由于与高速轴相连的太阳轮是完全轴对称结构，故而只考虑在行星齿轮处施加大小为35 kg/mm的不平衡量。施加弹簧支撑与不平衡量后的模型如图4所示。输出轴下端面和输入轴上端面随转速频率变化的振动幅值如图5所示。

图4 施加弹簧支撑与不平衡量后的模型Fig.4 The model of applying spring support and unbalance value

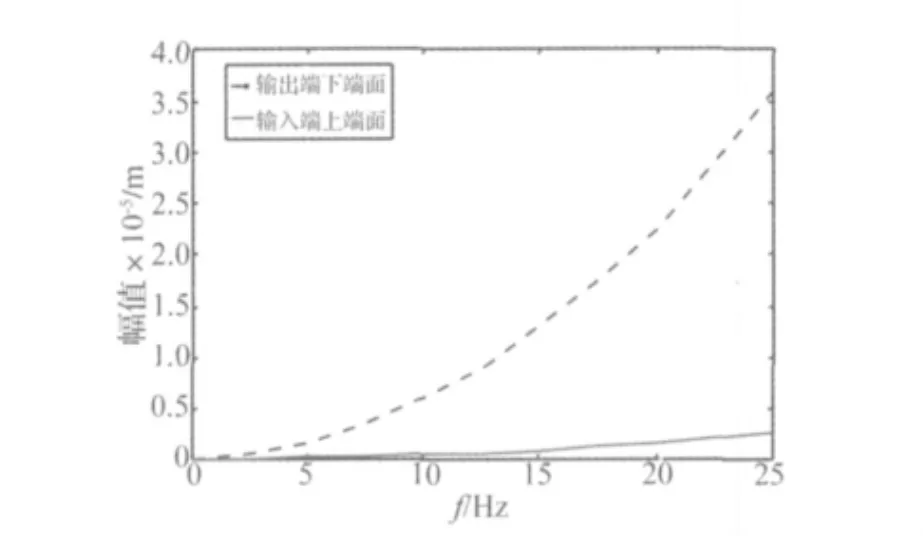
图5 最高转速为1 500 r/min的振动响应曲线Fig.5 The response curve of planetary gear train in the rotational speed of 1 500 r/min

从图5中可以看出，在额定输入转速994 r/min时，齿轮系统输入端上端面处最大不平衡振动幅值为1.1 μm，输出端下端面处最大不平衡振动幅值为15 μm。齿轮转子系统在不平衡激励下，在远远高于转子临界转速点出现临界响应峰值，说明转子转速有效的避开了临界转速，因此转子不平衡冲击对正常工况下齿轮箱的噪声影响可以忽略。

3 立式行星齿轮传动减速箱的边界元建模及辐射声场的计算

建立声学边界元模型。板壳类结构的声辐射主要是由板壳的弯曲振动引起的，面内纵向振动所引起的辐射噪声量相对于总噪声很小，因此在进行声场分析时主要考虑薄板结构的弯曲振动引起的噪声［6－7］。在建立边界元网格模型时，以对应薄板弯曲振动波的区域建立边界元网格，同时忽略筋板结构的振动声辐射。图6为用于辐射声场计算分析的边界元网格模型。

采用边界元法计算齿轮箱振动辐射声场，将ANSYS计算得到的稳态不平衡响应作为声场的激励导入LMS Virtual.lab计算其辐射声场。

图6 用于声场计算的齿轮箱边界元网格模型Fig.6 Boundary element model of gearbox for acoustic calculation

图7 齿轮箱辐射声场网格模型Fig.7 The mesh model of sound field radiated from gearbox

图8 齿轮箱壳体结构辐射声场声压级(dB(A))分布Fig.8 The distribution of sound field radiated from gearbox in sound pressure level

齿轮箱周围辐射声场分布在壳体等效辐射噪声实体周围区域，声场网格模边界元网格位置如图7所示。

本文计算声场的声传播介质是空气，计算中采用的空气介质的参数为:密度ρ=1.225 kg/m3，声音在空气中的传播速度v=340 m/s。在减速器壳体结构边界元网格外侧区域设置空气介质属性，图8显示了该齿轮箱的辐射声场声压级分布。

振动筛的优点是效率高，质量轻，系列完整多样，层次多，对于干煤炭筛分可以满足需求。缺点是对于原煤全水超过7%，振动筛所筛出块煤陷下率较高，工作时振动使煤炭更紧实的粘附于筛面，造成筛孔堵塞，筛分质量相对较差。

从图8的齿轮箱辐射声场声压分布中可看出，该齿轮箱整体在输入轴位置辐射的噪声较大，为80.4 dB(A)。

4 噪声测试试验设置及结果

按照该齿轮箱实际运行的工况要求，将齿轮箱垂向安置在试验机架上，机架顶部竖立安装电机，通过联轴器与电机连接，在工作现场对其在额定转速下进行了噪声测试，测试仪器采用IOTECH公司的 Wave-Book516E数据分析采集系统。根据对齿轮箱及机架的模态分析，取采样频率为10 kHz，采样时间为10 s［4－5］。

依据国标测量表面到最近的平面(包括墙壁和其他机器)之间的距离至少是测量距离两倍的规定以及关于声压级须在振动表面1 m远处测得的规定［8］，考虑到试验机架的内壁距离减速箱测试面的距离为1 m，因此定义噪声测量点的位置和减速机中轴线的距离为1.25 m。测点位置安排为:第1层测面为行星轮系(包括8个测点);第2层测面为上端第二对轴承的位置(包括8个测点);第3层测面为联轴器(包括8个测点)。

根据各噪声测点平面的频谱图以及对齿轮箱和机架的模态分析可以得出如下异常频率:

(1)16.6 Hz。在各噪声频谱图均出现此频率，通过计算分析可知，这个频率是电机的转频。

(2)142.7 Hz。在各噪声测点上均发现在142.7 Hz处存在幅值。进行模态分析后，得到机架在该频率处存在第17阶固有频率，其振型如图9所示。为验证该频率是否由机架低阶固有频率引起的谐振产生，对机架上若干特征点进行了振动响应的测试，结果表明机架两侧横向支撑梁上的振动响应最大。因此可以断定142.7 Hz正好是机架的第17阶固有频率。

图9 机架在142.7 Hz处的模态振型Fig.9 Mode shape of support bracket in 142.7 Hz

图10 齿轮箱在250.2 Hz处的模态振型Fig.10 Mode shape of gear box in 250.2 Hz

图11 机架在359 Hz处的模态振型Fig.11 Mode shape of support bracket in 359 Hz

(3)250.1 Hz。该频率处的噪声幅值在第3层测面上较为明显，经过与齿轮箱模态分析得到的在250.2 Hz处的模态振型图相比较得知:该频率下，齿轮箱发生轴向振动，因此在联轴器位置处的变形较大。据此可断定250.1 Hz为齿轮箱轴向振动模态，其模态振型如图10所示。

(4)359 Hz。从第1～第3层的频谱图中可以看到有359 Hz处存在峰值，通过与(2)相同的验证过程得到该频率为机架第63阶固有频率，模态振型如图11所示。

(5)640.3 Hz。在第1层噪声测面处发现该频率下出现幅值，经过与齿轮箱模态分析得到的640.269 Hz和640.70 Hz处的模态振型比较得知:齿轮箱在该频率下在靠近外圈处的变形较大，而噪声测面1恰好在侧面1的位置。据此断定640.3 Hz由齿轮箱的固有模态受激励产生，其模态振型如图12所示。

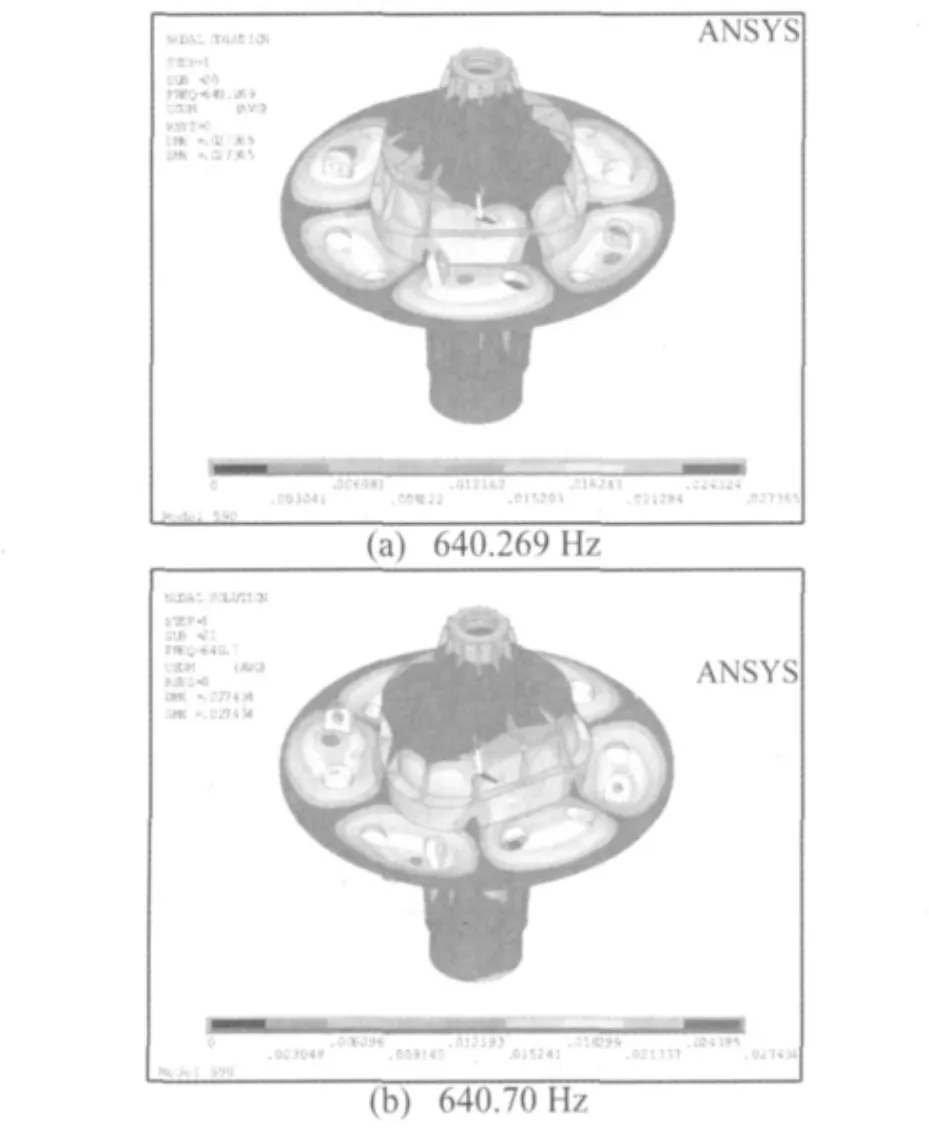
图12 齿轮箱在640.269 Hz和640.70 Hz处的模态振型Fig.12 Mode shape of gear box in 640.269 Hz and 640.70 Hz

(6)705 Hz。在各噪声侧点上均出现705 Hz左右的频率，与上类似，通过分析后得到705 Hz为机架的固有频率，模态振型如图13所示。

为表现上述6个异常频率，取第1层和第3层的测点声压频谱图如图14所示。

对于测试结果中出现的1 500 Hz以上的高频噪声，由于对减速机壳体的模态分析、齿轮系啮合频率以及电机转频的计算中都没有出现超过该数值的频率，又根据对试验机架的模态分析得知，该结构存在无限自由度，因此在高频时会与整体结构产生共振。另外，联轴器为一暴露于外部的旋转装置，在高速旋转时会与空气摩擦产生高频啸叫噪声，因此可以初步断定该高频噪声由以上两种因素产生，结果计算时可以通过高频滤波予以排除。

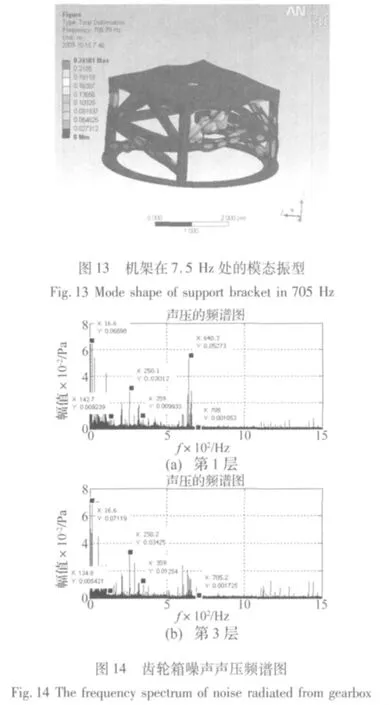
因为设置噪声测点位置时，由于受试验支撑机架尺寸的限制，测点距离测量基面的距离小于1 m，因此需对此噪声测量值进行距离修正，得到国标规定的距离测量基面1 m之外的噪声声压值［8］:

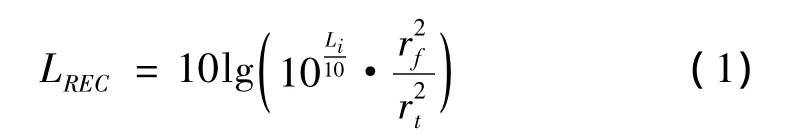
其中，Li、LREC分别为进行距离修正前后的噪声声压级，rf、ri分别为修正前后的测量点与减速机中心转轴的距离，各自为1.25 m、1.925 m。

根据国标中关于背景噪声修正的规定［8］，由于本测试中A计权背景噪声的声压级比测量得到的减速机正常运转时的声压级低9 dB左右，因此需选用修正值Ki对每个测量点的声压级数值进行由下式进行计算修正(国标规定，上述声压级差值在6～9 dB内时，Ki取值为1 dB;差值为3 dB时，Ki取值为3 dB)。修正公式为:

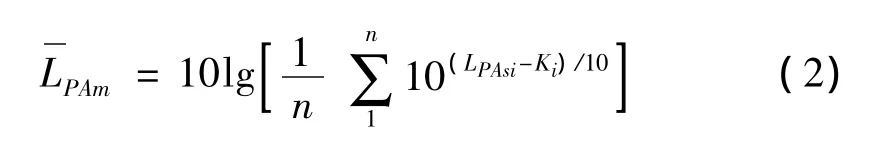
修正完后的各平面噪声数值如表1所示。

表1 齿轮箱辐射噪声声压级Tab.1 Sound pressure level of noise radiated from gearbox

基于以上噪声源的考虑以及测试环境的限制，对测量数据进行了高频滤波、背景噪声修正及测量距离修正，最终得到的在距离产品减速机基面1 m处柱面声压级噪声加权平均值为81.240 dB(A)。前面基于边界元计算得到齿轮箱辐射噪声声压级与该试验测试结果比较相差1.04%，说明了基于有限元和边界元的齿轮箱噪声计算分析有较高的准确性。

5 结论

针对行星齿轮传动中存在的振动和噪声问题，基于FEM和BEM分析方法，利用有限元分析软件ANSYS和声学分析软件LMS Virtual.lab对大型立式行星传动齿轮箱的模态和声场特性进行了计算分析，并在实际运行工况条件下对该齿轮箱进行了现场噪声测试。理论分析结果与试验结果都表明了该齿轮箱的噪声主要来源于齿轮箱内齿轮的啮合撞击，当激振频率接近系统的固有频率时产生的噪声较大，并且噪声声压级的计算预测结果与实测结果较为吻合，说明了理论计算的准确性和可行性。

［1］ 唐增宝，钟毅芳，周建荣.直齿圆柱齿轮传动系统的振动分析［J］.机械工程学报，1992，28(4):86－93.

［2］ Kahraman A.Natural modes of planetary gear trains［J］.Journal of Sound and Vibration，1994，173(1):125－130.

［3］ Lin J，Parker R G.Planetary gear parametric instability caused by mesh stiffness variation［J］.Journal of Sound and Vibration，2002，249(1):129－145.

［4］ 曹树谦，张文德，萧龙翔.振动结构模态分析－理论、实验与应用［M］.天津:天津大学出版社，2001.

［5］ 许本文，焦群英.机械振动与模态分析基础［M］.北京:机械工业出版社，1998.

［6］ 姜 哲.振动表面局部辐射性质与声能量辐射:I理论［J］.声学学报，1997，22，(6):534－542.

［7］ 闫再友，姜 楫，严 明.利用边界元法计算无界声场中结构体声辐射［J］.上海交通大学学报，2000，34(4):520－523.

［8］ 中国国家标准.GB/T 6404.1——2005/ISO 8579－ 1:2002齿轮装置的验收规范－第一部分:空气传播噪声的试验规范［S］.北京:中国国家标准化管理委员会，2006.

［9］ 郭 磊，郝志勇，蔡 军，等.汽车变速箱齿轮传动系动力学振动特性的研究［J］.振动与冲击，2010，29(1):103－107.

［10］ 陆 波，朱才朝，宋朝省，等.大功率船用齿轮箱耦合非线性动态特性分析及噪声预估［J］.振动与冲击，2009，28(4):76－80.