基于改进的串音误差的盲分离评价指标

李 宗，冯志鹏，褚福磊

(1.清华大学 精密仪器与机械学系，北京 100084;2.北京科技大学 车辆工程研究所，北京 100083)

为了对盲信号的分离结果进行评价，目前有多种盲分离评价指标，如描述全局矩阵和单位矩阵接近程度的串音误差［1］(性能指标PI)、测度源波形估计误差的二次残差［2］、评价分离信号与源信号相关程度的相关系数指标［3］等。在仿真实验中，多数指标需要找出与分离信号分量对应的源信号分量，但由于盲分离排序的不确定性，这在低信噪比时往往很难做到。串音误差不需要这种对应关系，能通过全局矩阵直接评价分离结果，是应用的最广泛的指标之一。但它对于各分量能量差异大的源信号和全局矩阵为某些非行元素优势矩阵的情况，往往不能给出和实际分离结果一致的评价。

本文通过构造全局权重矩阵和引入相关系数来改进上述不足。改进后的指标扩大了串音误差的使用范围，并能更准确有效的评价仿真实验分离结果。

1 串音误差定义及存在的不足

全局矩阵是分离矩阵和混合矩阵的乘积。在获得理想分离时，全局矩阵可以表示为置换矩阵和满秩对角矩阵相乘，即:

C=BA 理想情况下，G=PΔ

式中:A为混合矩阵，B为分离矩阵，Δ为满秩对角矩阵，P为置换矩阵。置换矩阵定义为每行和每列中只有一个元素等于1，而其他元素都为零的矩阵［4］。

串音误差用来衡量G接近对角化的程度，计算公式如下:

首先在文献［5］的基础上，引入如下概念。设矩阵G=［gij］∈Cn*n

通过全局矩阵G，我们可以建立估计信号y和源信号s的关系:

y=Bx=BAs=Gs

式中，x为观测信号。若写成分量形式则有:

如果源信号各分量能量差异不大，则PI越小，说明式(2)右侧某一项giksk越大于其他项，可以得yi(giksk，即信号得到很好的分离。但是，在源信号各分量能量差异大的情况下，较小的PI只表示gik远大于其他gij，j=1，2，…，k－1，k+1，…，n，并不表示 giksk远大于其他 gijsj，j=1，2，…，k－1，k+1，…，n。也就是说，在源信号各分量能量差异大的情况下，小的PI并不能说明分离结果好。

串音误差还存在另一个问题。文献［6］构造出了一些特殊的全局矩阵:

针对串音误差的这两个问题，本文通过构造全局权重矩阵和引入相关系数两种方法分别进行解决，并在最后将两种方法进行了综合。

2 改进方法

2.1 基于全局权重矩阵的串音误差改进

由上面分析可知，整体考虑giksk比只考虑gik更准确。所以我们将源信号各分量的能量平方根带入全局矩阵整体考虑，得到全局权重矩阵Gw:

在全局矩阵中引入权重:源信号各分量的能量平方根，即幅值，我们构造出了全局权重矩阵，由此得改进的串音误差Im1。Im1越小，说明式(2)中优势元素越显著，即式(2)右侧某一项giksk越大于其他项gijsj，j=1，2…，k－1，k+1，…，n，yi越接近单一源信号分量，分离结果越好。而PI越小，说明的是gik越大于其他gij，j=1，2，…，k－1，k+1，…，n，全局矩阵越接近对角阵或其置换阵。即PI评价的是全局矩阵和对角阵的接近程度，Im1评价的是 yi和 giksk(i=1，2，…n)的接近程度。Im1比PI更能准确反映分离结果。

2.2 基于相关系数的串音误差改进

对于如:

这样的全局矩阵，PI给出的结果过小，和实际分离结果大相径庭。因为，以(4)式为例，优势元素在同一列的情况下，估计信号各分量的说明见后面)得到的是对同一源信号分量s1的估计，这样的分离结果是非常差的。因此，要改进的是在这种情况下如何提高PI的结果。注意到，由于都是s1的线性组合，三者之间必然存在相关性。因此我们引入相关系数衡量各估计信号间的相关程度，并将其加入到PI的计算式中。这里需要注意的是，相关系数计算的是=Gs中的，而不是通过如FastICA等算法直接得到的y。具体计算流程如下:

(1)计算全局矩阵第一行和第一列的串音误差。和式(1)中计算第一行和第一列表达式相同。为了区分 PI，记为 Im2。

(2)判断全局矩阵第二行优势元素所在列，如果和第一行优势元素不在同一列，则用式(1)计算第二行和第二列串音误差。如果和第一行优势元素在同一列，引入相关系数来增大评价结果，得:

式中，ρ12是和的相关系数，α为设置参数，目前取为0.78，选取方法见后面分析。

针对学生的不同情况，定制不同的学习任务，明确奋斗的目标。上述三例中，小袁的学习方法欠缺，浅尝辄止，学的不扎实。学习任务中的读、写、练习集中在错例纠正上，学习目标是反复练习、巩固。小李、小江以技能赛英语词汇、句子训练为主要任务，重点完成技能赛必备知识、技能练习，以口语训练作为重点，配以写作练习。小李英语基本功稍好，要求高一些，小江底子薄，就从口语练习上突破，以读、背为主。在听力练习方面同步进行。由于为他们量身定制了不同的学习任务，三位同学都取得了良好的学习效果。

(3)判断全局矩阵第三行优势元素所在列，如果和前两行都不在同一列，则用式(1)计算第三行和第三列串音误差。如果和其中一行优势元素(如第一行)在同一列，则有:

如果三行优势元素都在同一列，则有:

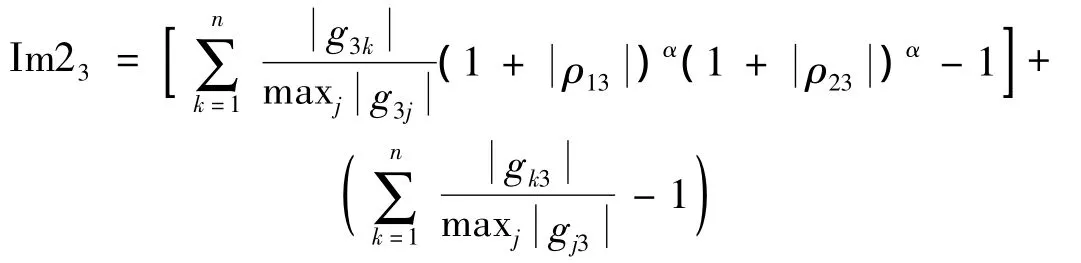
以此类推，最后得:

2.3 两种改进方法的综合

Im1提高了源信号能量差异大时评价的准确性;Im2提高了全局矩阵为某些非行元素优势矩阵时评价的准确性。因此，将两种方法综合，即用2.1中全局权重矩阵的元素gwij代替2.2计算流程中的gij，我们得到了应用范围更广、评价更准确的串音误差，记为IPI。IPI既考虑了源信号各分量的能量差异，又可以解决PI和Im1不能准确评价全局矩阵为某些非行元素优势矩阵的问题，因此评价最准确，给出的值最能真实反映分离结果。

2.4 四个指标的比较(表1)

表1 四个指标的比较Tab.1 Comparison of four indexes

3 仿真研究

3.1 Im1的仿真与比较

为了验证基于全局权重矩阵改进的有效性，构造源信号为常用仿真信号，由两个正弦波和一个方波组成，其中第一个正弦波的能量是第二个正弦波的100倍，能量差异大。

式中:f0=100。经矩阵A混合和SNR=5 dB加噪，然后进行分离，结果如下。

矩阵G中，第一行和第二行优势元素同列，第三行优势元素不显著，计算得PI=0.341 1值较大，即PI评价分离结果不好。实际上，由于s1和s3的能量远大于s2，所以评价分离结果时应考虑各gijsj的相对大小而不只是gij。观察Gw，Gw是行元素优势矩阵，各行优势元素显著，计算Im1=0.108 3值较小，即Im1评价分离结果是较好的。对比图1和图2可以发现估计信号基本重现了源信号的幅值和波形。Im1比PI评价的更准确。

3.2 Im2的仿真与比较

实验一，对式(4)计算 PI和 Im2，得 PI=0.0067，Im2=0.6733。可见Im2更准确的反映了分离情况。

实验二，为了减少源信号能量差异对评价的影响，调整3.1中仿真源信号幅值使各分量能量相等。

式中，f0=100 Hz。将s经矩阵A混合和SNR=10 dB加噪，然后进行分离。

计算得 PI=0.279 8，Im2=0.459 4。本例 PI小于3.1的PI=0.341 1，但从图3和图4可以看出，本例的分离结果没有3.1的好，PI给出的结果偏小。观察G，第二行和第三行的优势元素在同一列，对于这种非行元素优势矩阵，Im2中相关系数增大评价结果，计算得Im2=0.459 4是一个较大的值。和PI相比Im2更真实反映了本例的实际分离情况。

此外，我们可以看出，PI没有绝对的衡量标准，缺乏可比性。进而考虑Im1，本例中源信号各分量能量相同，所以Im1=PI=0.279 8，比上例的Im1大，即从Im1的值我们可推断本例的分离结果没有上例好。

3.3 IPI的仿真与比较

经矩阵A混合和SNR=［－10－5 0 5 10 15 20］dB加噪，共进行7组实验，并画出4种指标随SNR变化的图形，如图5所示。

分析图中的三个信噪比，SNR=－10、－5、0 dB。SNR从－10 dB到－5 dB和从－5 dB到0 dB，PI值基本均匀下降，IPI是先缓降再陡降。观察三种信噪比下分离信号波形，如图6～图8，SNR=－10 dB和SNR=－5 dB的分离信号波形相差并不大，改善效果不明显;而SNR=－5 dB和SNR=0 dB的分离信号波形相差大，改善明显。定量分析三个信噪比下分离波形的相异程度，计算输出信噪比指标:

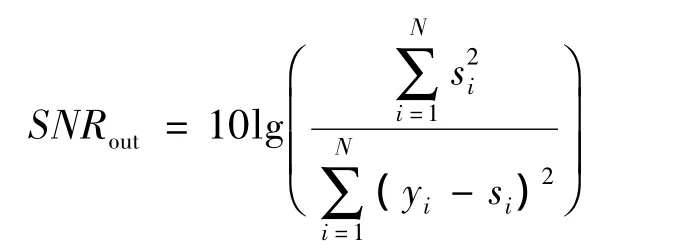
得:SNRout－10=0.813 5，SNRout－5=0.948 1，SNRout0=2.194 5。可知从SNR=－5到SNR=0分离结果的改善好于从SNR=－10到SNR=－5。IPI先缓降再陡降的变化趋势和此相吻合，IPI比PI评价的更准确。

此外，我们从图5上还可以得到其他一些信息。以SNR=－10为例，Im2＞PI说明G是非行元素优势矩阵。Im1＜PI说明源信号各分量能量有差异。IPI=Im1说明Gw是行元素优势矩阵。

3.4 真实信号分离结果评价

为了进一步验证评价指标IPI的有效性，下面用它对真实机械设备故障信号的分离进行评价。两个源信号为齿轮断齿故障信号和齿轮轻微磨损故障信号，混合信号如图10所示。

分别用sons算法和fastica算法进行分离，分离结果如图11所示，sons分离出的两信号差异大，且其中一个信号呈现幅值很大的有规律的冲击振动，显示出了断齿故障。fastica算法分离出的两信号差异小，无法正确判断信号对应的故障。再从断齿信号的频谱图(图12)分析，理论计算得断齿啮合频率为120 Hz，源信号幅频图上在120 Hz、180 Hz及240 Hz上均呈现大的幅值，sons分离结果和其一致，但fastica分离信号频谱上故障特征频率不明显。由以上分析可知sons分离结果比fastica更理想。用IPI评价分离结果，得IPIsons=0.557 1，IPIfastica=1.133 4，即 sons的分离结果远好于fastica。IPI的评价结果和信号表现一致，IPI正确的评价了分离结果。

4 故障诊断中常用算法评价

下面用IPI指标对机械设备故障诊断中的常用盲分离算法 FastICA，SOBI，SONS，JADE进行评价。旋转机械有2个关键零部件:轴承和齿轮。轴承支持机械的旋转部分，而齿轮使转动轴转速变化，依照旋转机械轴承和齿轮啮合振动模型［7］，构造仿真源为:

式中，s1为齿轮啮合信号，s2为轴承振动信号，fm=400 Hz为啮合频率，fb=170 Hz为与故障有关的特征频率，fr=20 Hz为轴的转速。用上述4种算法在SNR=［－10－5 0 5 10 15 20］dB下进行分离。

图13 IPI指标下常用算法随SNR变化的比较Fig.13 Comparision of common used algorithms with the variation of SNR by IPI index

图13中可以看出，从－10 dB到0 dB，SONS算法的分离性能最好。这是因为SONS算法对加性白噪声是非常稳健的。SOBI算法虽然对于不同功率谱的源信号有好的分离，但是由于源信号中有白噪声，所以分离结果次于SONS算法。FastICA和JADE算法对白噪声不稳健，在低信噪比时表现不理想。从0 dB到10 dB，随着信噪比的增大，JADE法和FastICA的良好分离性能得以发挥，分离结果接近或超过其他两种算法。随着信噪比的继续提高，各分离算法分离结果差异不大，基本都能很好的分离信号。

所以，对于低信噪比信号，优先考虑使用SONS算法进行分离。对于高信噪比信号，各分离算法分离效果接近，由于FastICA结构简单，收敛速度快，优先考虑使用。

5 结论

现有的盲分离评价指标串音误差评价的是全局矩阵对角化的程度，在源信号各分量能量差异大或全局矩阵为某些非行元素优势矩阵时评价结果不准确。本文通过构造全局权重矩阵直接评价分离结果、引入相关系数处理非行元素优势矩阵，解决了上述问题，并将两种方法进行了综合，提高了评价的准确性，扩大了串音误差的应用范围。寻找绝对的衡量标准，使得改进的指标在处理不同问题时具有更可靠的可比性是要进一步研究的内容。

［1］ Cichocki A，Amari S I.Adaptive Blind Signal and Image Processing［M］.New York:John Wiley ＆ Sons，INC，2002:161－161.

［2］ 焦卫东.基于独立分量分析的旋转机械故障诊断方法研究［D］.杭州:浙江大学，2003.

［3］ 肖文书，张兴敢，都思丹.雷达信号的盲分离［J］.南京大学学报，2006，42(1):38－43.

［4］ Hyvarinen A，Karhunen J，Oja E.Independent component analysis［M］.New York:JohnWiley ＆ Sons，INC，2001:281.

［5］ 徐明彪，朱维彰.关于信号盲分离分离效果评判指标的分析［J］.杭州电子工业学院学报，2002，22(3):177－180.

［6］ Mansour A，Kawamoto M，Ohnishi N.A survey of the performance indexes of ICA algorithms［C］//.Proceedings of the IASTED International Conference Modeling，Identification，And Control，Innsbruck，Austria，2002:660－666.

［7］ Ypma A.Learning methods for machine vibration analysis and health monitoring［D］.Delft University of Technology，2001.