SGWP算法在爆破振动信号分析中的应用研究

谢全民，龙 源，郭 涛，张怀智，路 亮，张洋溢

(1.解放军理工大学 工程兵工程学院，南京 210007;2.武汉军械士官学校 弹药修理与销毁教研室，武汉 430075;

3.广州军区工程科研设计所，广州 510515)

爆破振动信号分析是研究控制爆破振动危害的基础，也是科学制定抗震措施的前提［1－3］。因爆破振动导致结构破坏是动力响应过程，为使爆破振动安全标准更加科学化、合理化，须建立综合考虑振动强度、频率和持续时间等多因素的复合判据，要求在爆破振动信号分析中对信号本身蕴含的时频、能量等重要特征信息进行准确提取。考虑到爆破振动监测过程中易受外部环境和测试系统的影响，实测数据中常含噪声干扰［4］，因此为测试数据探寻有效的噪声去除算法，可提高爆破振动测试信号特征提取的可靠性和准确性。

工程爆破中为建立大型网络化测试系统与控制平台，实现爆破振动智能化监测与预报的工程应用目的，要求在傅里叶变换、一代小波变换等传统信号处理技术基础上提高信号分析处理的效率和质量，满足在线处理对算法效率、精度等方面的要求。

Sweldens［5］提出的提升算法被称作二代小波变换，在继承经典小波多分辨分析特性的基础上，可实现数据原地运算，具有占用空间小，变换速度快等优势。相同数据长度下运算速度提高近50%。采用二代小波变换技术可通过设计不同的预测算子和更新算子得到具有某些特殊性能的小波函数［5－6］，脱离傅里叶变换的局限性，更好地适应待分析信号特征。

目前二代小波变换主要应用于机械振动信号分析、故障诊断等方面［7－10］，但在爆破振动信号分析中的应用尚未见相关研究报道。考虑到小波包变换技术在信号处理方面能够更加完整地保留爆破振动信号局部化特征，同时可提取指定频率区间的小波包分量进行主分量特征分析［2，11］，本文构造了基于插值细分法的二代小波SGW(6，6)，对二代小波包(Second Generation Wavelet Packet，SGWP)变换在爆破振动信号噪声滤除及频谱、能量等重要特征提取中的应用进行了有益的探索，取得了较为满意的效果。

1 SGWP算法及SGW构造

1.1 SGWP算法

(1)剖分:对第(j，n)(n=1，2，…)，2j节点系数进行奇偶分裂为

(2)预测:由式(1)得到第(j+1，2n)节点的系数。

式中:p［l］(l=1，2，… ，N)为预测器系数。

(3)更新:由式(2)得到第(j+1，2n+1)节点的系数。

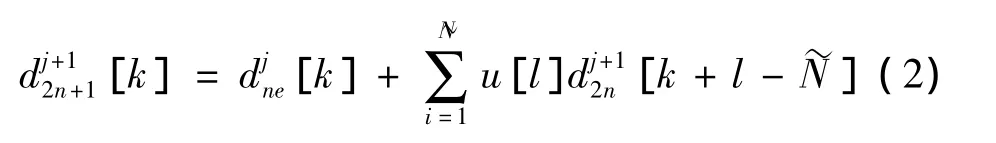
式中:u［l］(l=1，2，… ，N～)为更新器系数。

1.1.2 重构算法

(1)反更新:由(j+1，2n)，(j+1，2n+1)节点系数求 (j，n)节点的偶系数。

(2)反预测:由(j+1，2n+1)节点系数和(j，n)节点的偶系数求(j，n)节点的奇系数。

SGWP变换两级分解与重构过程如图1所示。

图1 SGWP两级分解与重构示意图Fig.1 Two levels decomposition and reconstruction based on SGWP

表1 预测系数Tab.1 Predict coefficients

1.2 SGWP改进算法

对信号进行SGWP变换是逐层隔点采样，每进行下一个分解尺度变换时，采样率会降低1/2，当高频部分不满足采样定理［11］时易发生频率折叠，同时由于SGWP算法等效的滤波器为有限长度，不可能具备理想的频率截止特性［10］，上述因素导致变换过程易出现混频现象，使分析结果失真。文献［12－13］中研究了小波包变换的频率混叠问题，并通过移频处理技术改进二代小波包变换算法。

分解算法式(1)、式(2)变为:

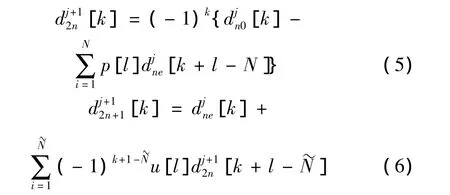
重构算法式(3)、式(4)变为:

1.3 SGW 构造

若已知序列 x0，x1，…，xN对应函数值为 y0，y1，…，yN，且满足yi=f(xi)(i=0，…，N)，则存在唯一1个次数不大于 N的多项式 Ln(x)，使得 Ln(xi)=f(xi)，那么:

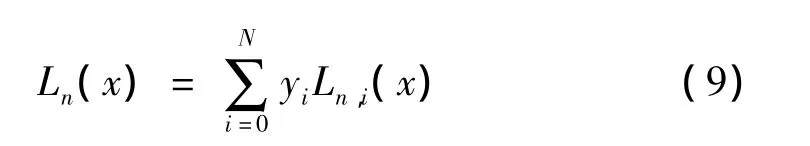
其中:

每次进行插值细分时，取N个(N=2D，D∈Z+)等间隔样本 yj，k－D+1，…，yj，k，…，yj，k+D，，其对应的采样时刻为xk+1，xk+2，…，xk+N，xk为任意起始时间。通过细分产生新的采样值处于已知样本中间，插值点为:x=xk+(N+1)/2，则预测系数可由式(11)确定，即:

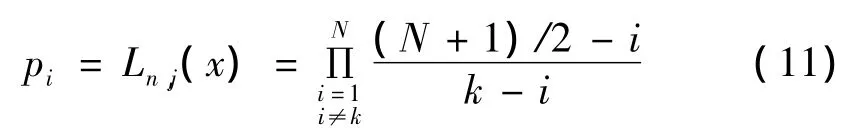
当N=6时，根据式(11)计算其对应预测系数如表1所示。

设信号S为一个σ序列，即:

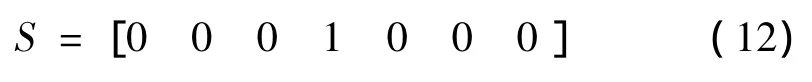
首先构造尺度函数。由剖分原理及图1中的小波包重构部分对序列S进行插值细分，即利用k－1，k，k+1，k+2 四点的 sj，k值预测 sj+1，2k+1，插值边界采用补零的方法进行处理，经过18次迭代可得尺度函数。

下面构造小波函数。首先需要设计更新算子U，因更新算子是为保证小波变换前后信号的低阶消失矩不变，当N=N～(N为预测器的个数，为更新器的个数)时，可直接将预测系数除以2作为更新系数［14］。

其中:

式中，U和D分别为更新算子运算系数和细节信号序列。与尺度函数的构造类似，设细节信号为σ序列，近似信号S为零序列，进行一次提升格式反变换，信号的偶序列为:

该序列经过预测算子p(·)进行恢复预测运算，得到信号的奇序列为:

对s0进行插值细分，经过18次迭代可得到相应的小波函数。

基于提升算法构造的尺度函数和小波函数是双正交、对称、紧支撑的，且具有冲击形状［5，14－15］。当 N 和N～较小时，尺度函数和小波函数的支撑区间较小;反之，支撑区间较大，具有较好的连续性。实际应用表明，支撑区间较小的小波函数适宜于处理非平稳信号，而支撑区间大且连续较好的小波适合于描述稳态信号［13］。爆破振动信号具有典型的短时非平稳特性［1－4，11］，研究过程中发现 SGW(6，6)适宜于爆破振动信号分析。

2 基于SGWP改进算法的爆破振动信号去噪

图2为爆破振动实测信号S1，信号采样频率fs=1 024 Hz，采样点数n=2 048。从爆破振动时程曲线图2可知，振动波形中混杂有毛刺以及由于测试系统本身带来的方波干扰。图3为测试信号S1降噪前的三维时频谱，分析可知该测试信号中混杂有200～250 Hz频段内的高频噪声分量。

图2 实测爆破振动含噪信号Fig.2 Measured vibration signal with noise

2.1 SGWP降噪算法

基于SGWP变换的爆破振动测试信号降噪过程如下:

(1)采用移频算法改进的SGWP技术对测试信号进行满二叉树的多分辨分解;

(2)对于给定的信息代价函数，选择最优的二代小波包基;

(3)对最优基分解所得的各节点系数进行阈值量化;

(4)逐层对阈值处理后的节点系数进行重构;(5)去噪效果分析。

2.2 基于最优基的SGWP分解

采用1.3节中构造的插值小波SGW(6，6)，根据式(5)、式(6)对S1进行分解层数为3层的满二叉树分解。选用对数能量熵［13］作为信息代价函数，通过对各小波包变换系数的信息熵进行最优基搜索，完成二叉树的修剪，确定最优分解结构如图4所示。

2.3 节点系数阈值量化

为充分保留爆破振动测试信号时频特征的局部特性，选择Donoho等［16］提出的软阈值法进行节点系数的阈值量化。

其中，N为小波包系数长度，j为分解尺度。

式(18)中爆破振动信号的噪声方差σ未知，按下式进行估计:

其中，median［·］为中值函数。

根据式(17)～式(19)，可对各节点小波包系数进行软阈值处理。

2.4 去噪效果分析

图 5 为图 4 中确定的最优基 d10，d11，d20，d21，d2，2，d23，d30，d31，d32，d33，d36，d37对应的二代小波包变换系数。对上述对应的小波包系数阈值处理后再进行逐层重构，即得到降噪后的爆破振动信号，波形曲线如图6所示。

图5 基于SGW(6，6)最优基分解小波包变换系数Fig.5 Optimum wavelet packets coefficients based on SGW(6，6)

从图6中滤波后的振动波形可以看出，采用基于SGWP变换的软阈值去噪算法已基本消除了爆破振动监测信号中由于测试系统和环境噪声带来的干扰。降噪后的时程曲线图6相对图2中降噪前的爆破振动波形曲线而言更为光滑，且峰值、波形上升和衰减等振动信号局部特征在降噪后的振动信号中表现得更加清晰，所得的有用信息图6中包含了更多能够客观准确地反映实测信号的主要成分，为进一步提取爆破振动信号特征提供了更加有效的信息。

图6 降噪后的爆破振动信号Fig.6 Blasting vibration signal after de－noising

为定量评价SGWP算法在爆破振动信号去噪分析中的应用效果，引入均方根误差(RMSE)、信噪比(SNR)、峰值误差(PE)等三项评价指标。

根据式(20)～式(22)计算得到图6中降噪后的爆破振动信号相对于图2中的实测爆破振动信号:RMSE= 0. 091 9， SNR =25.239 3，PE=0.028 15。可见，基于 SGWP算法的爆破振动信号去噪获得了较高的信噪比，且降噪前后误差较小。

图7 降噪后时频谱Fig.7 Time－frequency energy spectrum after de－nosing

3 基于SGWP的爆破振动信号特征提取

3.1 能量特征提取

爆破振动输入到附近建(构)筑物中的振动能量是导致结构失效、破坏的重要因素，采用SGWP改进算法研究爆破振动信号小波包频带相对能量分布特征的思路如下:

设爆破振动采样信号{s［i］}(i=1，2，3，4，…，2N)，N∈Z+。经分解层数j=3的SGWP改进算法分解后，第(j，n)节点的系数记为djn［k］(k=1，2，3，4，…，2N－k)。

定义归一化能量:

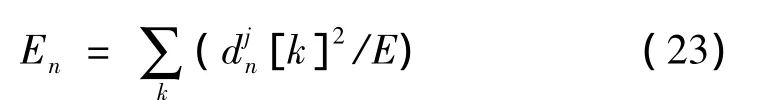
式中，E为信号总能量，即利用E对各频带内能量进行归一化，相应的特征向量称为归一化特征向量:

图8 典型的爆破振动时程曲线Fig.8 Time－curve of blasting vibration

图8为场地实验中采用单孔单段起爆方式时采集到的爆破振动信号S2，采样率为1 024 Hz，采采样点数n=1 024。S2已按第2节中的去噪算法滤除了噪声分量，表现出典型的冲击加载瞬态响应和运动特征。

图9为该信号的功率谱曲线。由功率谱图分析可知 S2的主振频率处于38～80 Hz、80～122 Hz及150～180 Hz三个频带区间。200 Hz以上的频率部分包含的功率谱密度较小，谱图中的分辨率较低，因此图中只给出了0～256 Hz范围内的功率谱密度分布情况。

根据式(5)、式(6)，采用 SGW(6，6)对 S2进行三层小波包分解，得到8个小波包d30～d37，相应的小波包系数如图10所示。

图9 功率谱Fig.9 Power spectrum

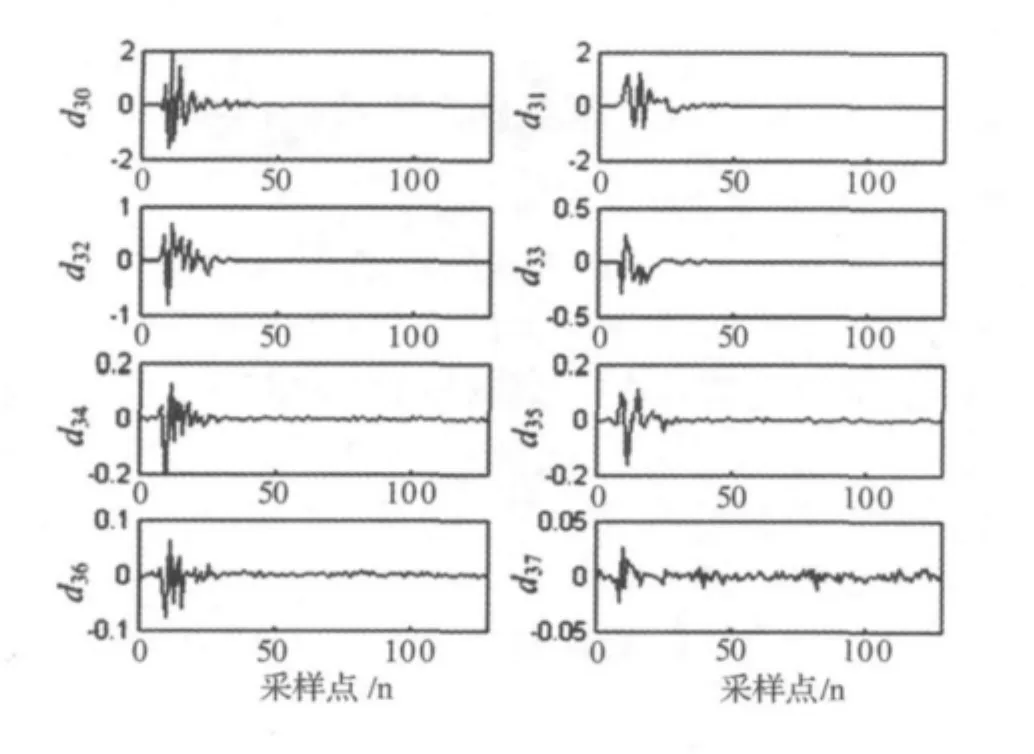
图10 d30～d37层提升小波包系数图Fig.10 Lifting wavelet packets coefficients of d30～ d37

图11是按式(23)、式(24)计算得到8个小波包对应的归一化能量分布。根据图11相对能量分布易知，爆破振动信号的优势能量主要分布在d30，d31，d32三个小波包对应的频带内，d33～d37对应频带包含的能量较小，与图9中功率谱密度分布情况一致。由于建(构)筑物的固有频率一般较低，当爆破振动能量分布趋于低频带时容易引发建(构)筑物共振而加剧破坏。因此，在爆破工程中可采用SGWP技术快速准确地获取原始信号中不同频率成份对爆破振动作用的影响，并用以指导爆破安全设计。

3.2 时频特征提取

图11 相对能量分布Fig.11 Relative energy distribution

为研究爆破振动信号中不同频率成份分量的振动响应机理，需掌握不同频率分量随时程变化产生的幅值衰减、频谱变化等规律，可通过提取指定频带范围内的振动分量进行研究。

实际应用中选取能量占优、且频段处于原爆破振动信号主振频带范围的二代小波包作为爆破振动信号的主分析小波包。根据图11相对能量分布，选取d30，d31，d32三个主分析小波包作为该信号的特征包。

对上述三个主分析小波包分量，根据式(7)、式(8)分别进行单支重构，即将其余节点系数置0，按照移频算法改进的二代小波包重构步骤进行小波包重构，分别获得对应的振动分量如图12(a)所示。该图体现了爆破振动测试信号S2主振频带分量的峰值出现时刻及时程衰减规律。d30代表的低频分量衰减较慢，振动持续时间较长;d32代表的高频分量衰减迅速，振动持续时间较短。

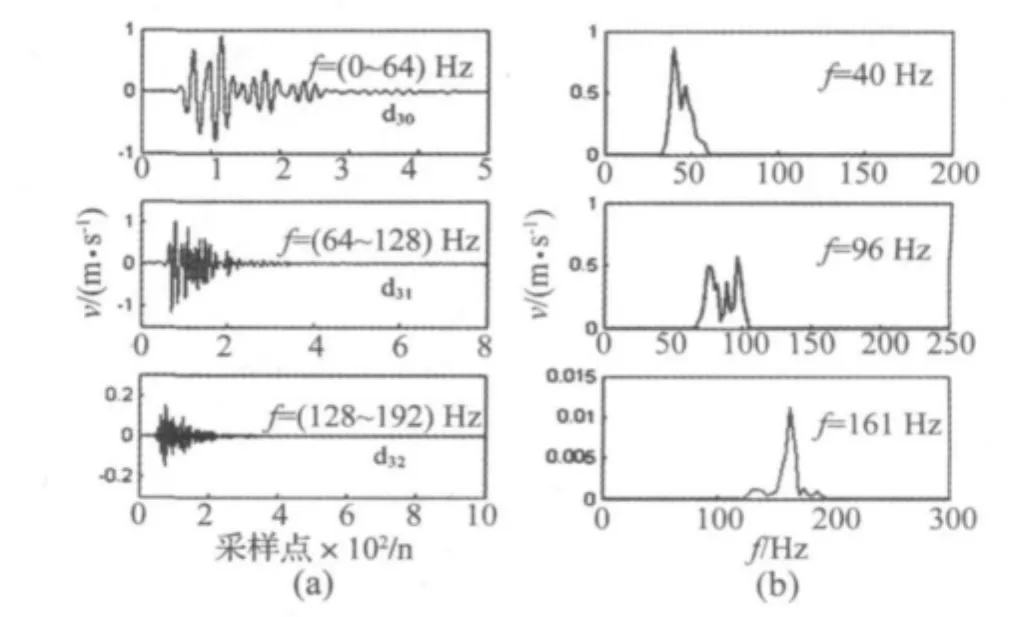
图12 三个主分析小波包单支重构及频谱分析Fig.12 Reconstruction of main wavelet packets and spectral analysis

分别对d30～d32重构所得的振动分量再进行FFT变换作频谱分析如图12(b)所示。由图12(b)中频谱特征可知三个小波包代表的振动分量均具有一定的频带宽度，且采用改进后的SGWP算法将原信号按独立的频带区间进行了比较精确地划分，基本避免了传统小波包变换过程中容易出现的混频现象，提高了频域分析精度。

综合分析图9、图12发现:三个主分析特征包分别对应频段d30(0～64 Hz)、d31(64～128 Hz)、d32(128～192 Hz)，三个特征包重构分量的频谱分别具有峰值f0=40 Hz，f1=96 Hz，f2=161 Hz。由此可见，爆破振动信号的主分析频带内存在两个或多个明显的优势频带区间，共同构成爆破振动信号的主振频带;同时根据能量的集中程度，可定义爆破振动信号中存在第一、第二、…主频率。尽管三个主分析小波包所表征的振动分量幅值和能量存在差异，但上述小波包代表的振动分量处于原信号中能量占优的频带区间，且体现的振动衰减特性和频谱特征均符合爆炸冲击响应规律，因此可采用其作为原信号的特征包描述爆破振动测试信号的时频特征。

可见，SGWP算法利用其在信号分析领域中特有的局部化分析能力，快速准确地提取到了爆破振动信号中主振频带内的振动分量，可为爆破振动作用下结构的动态响应分析及抗震对策制定等方面提供数据参考。

4 结论

(1)基于改进的SGWP技术能够快速有效地滤除爆破振动测试信号中包含的噪声分量，更多地保留测试信号的有效成分，为爆破振动信号特征的精确提取奠定了基础。

(2)采用SGWP算法成功获取了爆破振动信号的时频特征、能量特征，其良好的局部化处理能力适宜于具有短时、非平稳特性的爆破振动信号特征提取。

(3)SGWP算法具有速度快，精度高，易于实现等优点，在爆破振动效应分析领域具有较好的应用前景，为构建爆破振动大型网络化测试系统与控制平台提供了适宜的数据分析技术。

［1］ 谢全民，龙 源，田作威.爆破振动信号时频特征的三维分形特性研究［J］.振动与冲击，2010，29(12):122－126.

［2］ 谢全民，龙 源，钟明寿.小波包与分形组合技术在爆破振动信号分析中的应用研究［J］.振动与冲击，2011，30(1):11－15.

［3］ 娄建武，龙 源.爆破震动信号的特征提取及识别技术研究［J］.振动与冲击，2003，22(3):80－83.

［4］ 中国生，徐国元，江文武.基于小波变换的爆破地震信号去噪的应用［J］.中南大学学报(自然科学版)，2006，37(1):155－159.

［5］ Sweldens W. The lifting scheme:a custom－design construction of biorthogonal wavelets［J］.Applied and Computational Harmonic Analysis，1996，15(3):186－200.

［6］ 耿艳峰，冯叔初.小波构造综述［J］.石油大学学报(自然科学版)，2004，28(1):127－131.

［7］ 粟 鸣，郭东敏，权建峰.基于提升小波的改进半软阈值降噪方法［J］.探测与控制学报，2009，31(4):54－57.

［8］ 段晨东，何正嘉.基于提升模式的特征小波构造及其应用［J］.振动工程学报，2007，20(1):85－90.

［9］ 段晨东，李凌均，何正嘉.第二代小波变换在旋转机械故障诊断中的应用［J］.机械科学与技术，2004，23(2):224－229.

［10］ 周 瑞.基于第二代小波的机械故障信号处理方法研究［D］.哈尔滨:哈尔滨工业大学，2009.

［11］ Xie Q M，Long Y.Blasting vibration signal comparative analysis based on wavelet and wavelet packet technology［C］.The 2th Aisa－Pacific Symposium on Blasting Technology，2009:513－519.

［12］ 刘世元，杜润生，杨叔子.小波包改进算法及其在柴油机振动诊断中的应用［J］.内燃机学报，2000，18(1):11－16.

［13］ 曹建军.基于提升小波包和改进蚁群算法的自行火炮在线诊断研究［D］.石家庄:军械工程学院，2007.

［14］ Sweldens W，Schröder P.Building your own wavelets at home［DB/OL］.http://cm.bell－ labs.com/who/wim/papes.html/athome，1998－01－05.

［15］ Sweldens W.The lifting scheme:a construction of second generation wavelets［J］.SIMA J Math Anal，1996，29(2):511－546.

［16］ Donoho D L，Johnstone I M.Adapting to unkown smoothless via wavelet shrinkage［J］.J.Amer.Statist.Assoc.，1995，90(432):1200－1224.