转子轴系弯扭耦合振动的次同步谐振分析

李 军，陈予恕

(哈尔滨工业大学 航天学院，哈尔滨 150001)

随着社会经济的发展，人们对电力的需求越来越旺盛，这使得汽轮发电机组的研制、生产向巨型化、大容量的方向发展，相应的汽轮发电机组的振动问题也越来越突出。在实际的汽轮发电机组中，由于质量不平衡和外激励等多种因素的存在，从而导致汽轮发电机组的弯扭耦合振动问题越来越突出。所以在对系统进行动力学分析时，有必要考虑系统的弯扭耦合振动问题。在最近几十年，有一批关于转子弯扭耦合振动方面的研究出版Al-Hussain等[1－2]分别应用拉格朗日函数，建立了考虑平行不对中和倾角不对中的弯扭耦合转子系统的数学模型。在平行不对中的研究中得出:平行不对中能引起扭转振动和侧向振动;在倾角不对中的研究中，以倾角不对中对系统稳定性的影响为研究对象，得出:倾角不对中增加或者耦合刚度增加，系统的稳定区域也相应的增加。Papadopoulos等[3－4]建立了三自由度Timoshenko梁的弯扭耦合振动方程，研究了自由振动轴的动力学响应，分析表明:弯曲振动对扭转振动有很大的影响。刘占生等[5]建立了Jeffcott转子的非线性弯扭耦合模型，并对该系统在较宽的参数域内进行了分岔分析，得出不平衡量是判断什么时候发生弯扭组合共振的决定条件。弯扭组合共振可能引起系统潜在的不稳定，应该尽量避免系统参数选在弯扭组合共振区间。

我国的电力需求逐年增加，有时需要长距离和大容量的输送电能。为了提高传输效率和减少电路的损耗，常常应用串联补偿线路。然而这将有可能引起次同步谐振(sub-synchronous resonance)。次同步谐振是严重的电网问题，当满足次同步谐振的条件时，电网和发电机将发生剧烈的能量交换，可以引起汽轮发电机组轴系的大幅振动。因此专家学者对次同步谐振现象做了大量的研究。IEEE次同步谐振工作小组[6－7]分别于1977年和1985年给出了适合计算机计算的次同步谐振模型。向玲等[8－10]以串联补偿电力系统为研究对象，建立了机电耦合作用下的轴系扭转模型，结论表明:补偿度是次同步能否持续的重要因素，补偿度越高，电力系统中的次同步谐振电流越大，次同步谐振发生的危害性越大。刘超等[11]研究了轴系在次同步谐振作用下的扭转振动以及危险部分的疲劳寿命，分析了次同步谐振的振幅和扰动频率对轴系疲劳寿命的影响。

在以往次同步谐振对汽轮发电机组轴系振动的研究中，考虑轴系扭转振动的文献较多，考虑弯扭耦合振动的文献并不多见，周桐等[12]建立了考虑弯扭耦合作用时，汽轮发电机转子轴系和电网耦合次同步的非线性模型，分析了在不同偏心条件下弯曲振动和扭转振动的相互影响，并给出了弯曲刚度对系统稳定性的影响，向玲等[13]分析了次同步谐振机电扭振相互作用的原因，并设计了汽轮发电机组模拟系统的次同步谐振试验，分析表明，次同步谐振下轴系的弯曲振动和扭转振动是相互作用的。在次同步谐振情况下，引起扭转振动振幅增加的同时，弯曲振动的幅值也会相应的随之变化。本文所建立的低压缸转子和发电机转子弯扭耦合振动的非线性动力学模型。主要考虑在次同步谐振作用下，转子轴系的弯扭耦合振动问题，应用平均法得到系统的分岔方程，应用奇异性理论分析了系统的转迁集和分岔特性。最后应用数值算法分析了系统的运动特性。分析结果可以为该系统的参数选择和故障诊断提供理论依据。

图1 转子模型Fig.1 Model of rotor system

1 建立模型

以汽轮发电机组的低压缸和发电机转子为研究对象，如图1所示，将发电机和低压缸转子简化为两个圆盘，两个圆盘之间通过等效的无质量有有限刚度的元件相连接，考虑转子的弯扭耦合振动。另外当串联电容补偿的电力系统受到扰动发生电感电容谐振，其谐振频率与汽轮发电机组的轴系扭振某一振型的频率之和接近或等于系统的同步频率时，电气系统与汽轮发电机轴系之间可能会产生次同步频率功率交换。因此本文考虑了次同步谐振对汽轮发电机转子轴系的影响。

系统的坐标向量为{q}=[x1，y1，θ1，x2，y2，θ2]T，其中 x1，y1，x2和 y2分别为圆盘 1 和圆盘 2 在 x和y方向的弹性位移，θ1，θ2分别为两圆盘的弹性扭转角，e1和 e2为两个盘的偏心，和是弹性角速度。

系统的动能为:

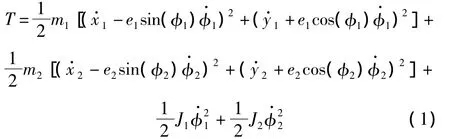
其中:φi=ωt+θi(i=1，2)，ω 为转子的同步频率。

系统的势能为:

应用拉格朗日函数L=T－V，和拉格朗日方程:

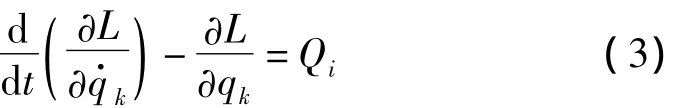
并对微分方程进行无量纲化处理，令X1=x1/c，Y1=y1/c，X2=x2/c，Y2=y2/c且 τ=ωt，其中 c为轴承半径间隙，可得系统的无量纲方程:

无量纲参数如下:

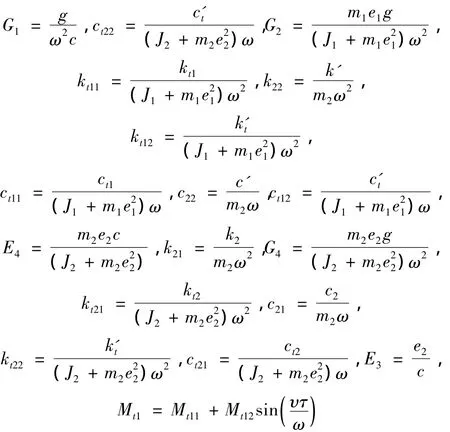
其中:m1，m2分别为两个等效圆盘的质量，J1，J2分别为两个等效圆盘的转动惯量，k1，k2，k'分别为发电机转子的刚度系数、低压缸转子的刚度系数和两盘之间的刚度系数。c1，c2，c'分别为发电机转子的阻尼系数、低压缸转子的阻尼系数和两盘之间的阻尼系数。kt1，kt2，k't分别为发电机转子的扭转刚度系数、低压缸转子的扭转刚度系数和两盘之间的扭转刚度系数。ct1，ct2，c't分别为发电机转子的扭转阻尼系数、低压缸转子的扭转阻尼系数和两盘之间的阻尼系数。Fx1，Fx2，Fy1，Fy2分别为x方向和y方向的外力，Mt1为电网次同步谐振引起的作用于发电机转子上的扭转力矩，并且υ=ωfωfs，ωf是同步频率，ωfs电力系统的固有频率。

从方程(4)可以看出，系统的弯扭耦合主要是由不平衡质量引起的，并且由于不平衡质量的存在，系统是非线性的。

2 解析分析

应用平均法[14]求解系统的响应，引入如下的变换:

可以将系统转化为典则形式:

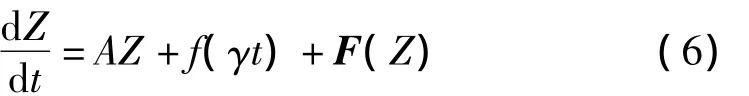
其中:向量F(Z)包含阻尼和非线性力。

模型(6)的无阻尼线性系统为:

方程(7)不含阻尼项，所以矩阵A仅含有纯虚根± iω1，± iω2，± iω3，± iω4，± iω5，± iω6。方程(7)的齐次部分的解可以写为:

其中:Pmi和Qmi为实常数。

方程(7)齐次部分的共轭方程可以描述为:

方程(9)的解可写为:

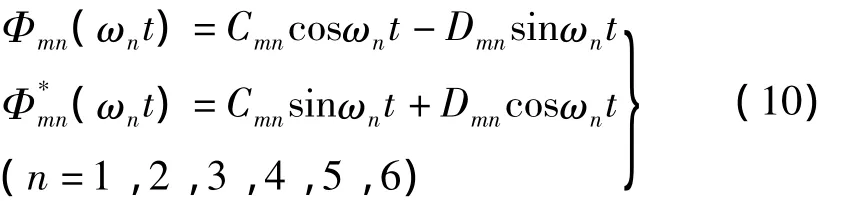
引入下列变换:

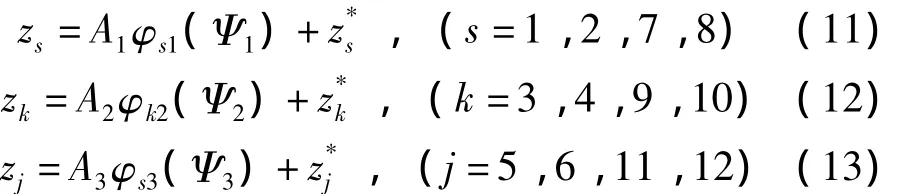
其中:φmi=PmicosΨi－ QmisinΨi，(m=s，i=1;m=k，i=2;m=j，i=3)并且是方程(7)的特解。如果Ai=cosst且，方程(11)、(12)和(13)是方程(7)线性齐次部分的解，因此:

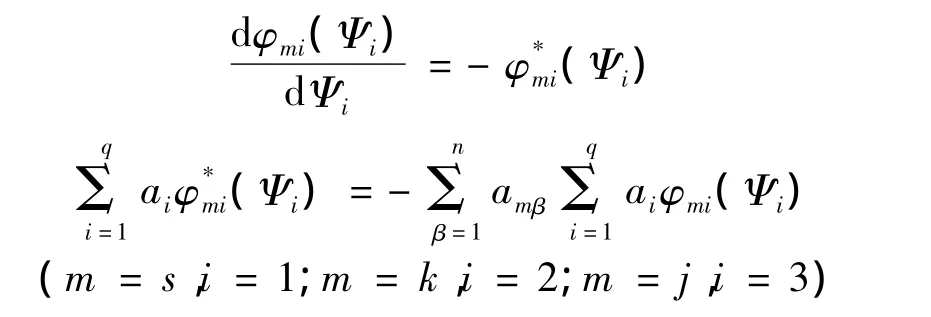
因为存在非线性部分，所以Ai≠cosst和2，3)。将方程(11)、(12)和(13)代入方程(6)可以得到:

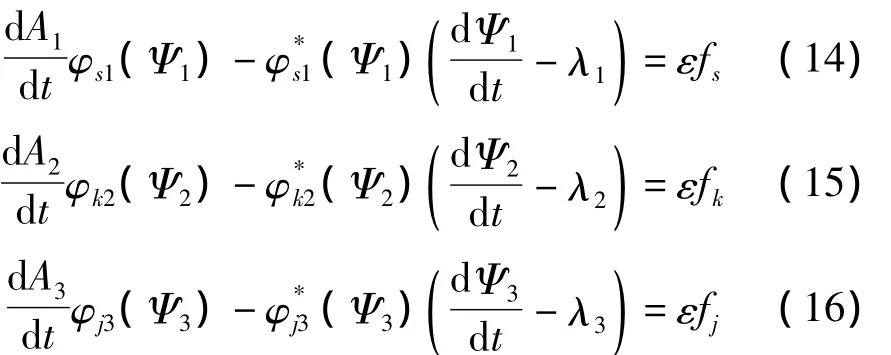
方程(8)和(10)存在正交性:

其中:

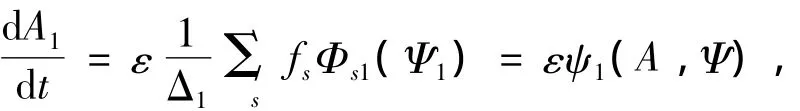
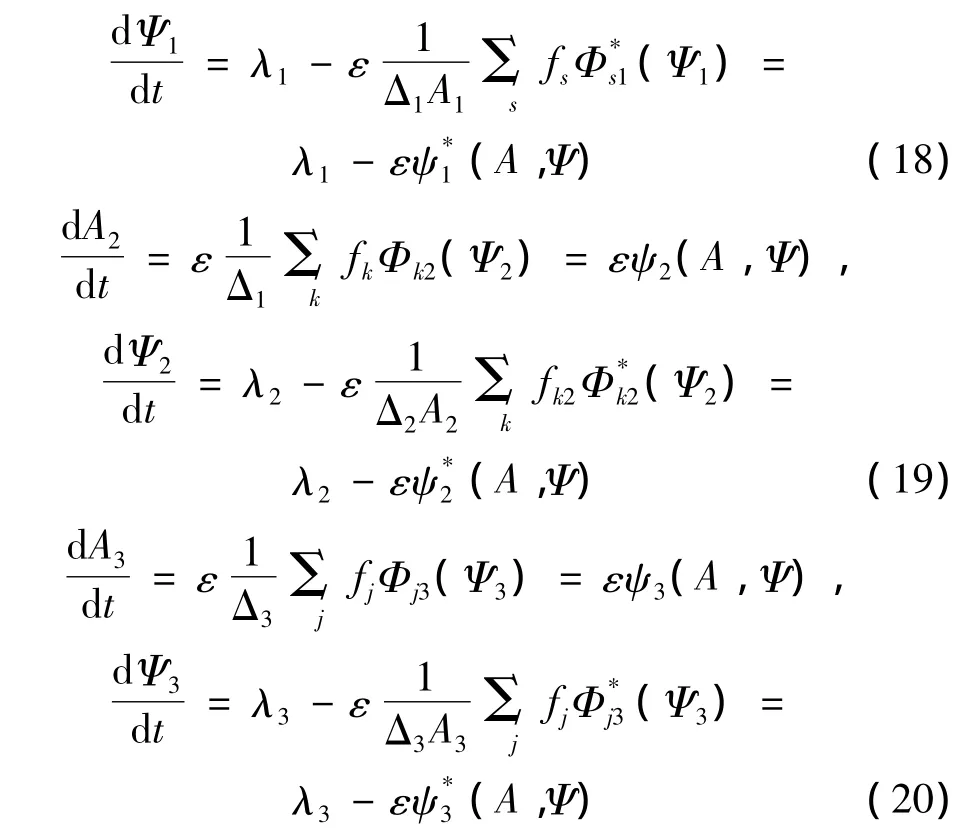
其中:

λ1和λ2是弯曲的前两阶固有频率，λ3是扭转的第一阶固有频率。

方程组(7)的齐次部分的解为:

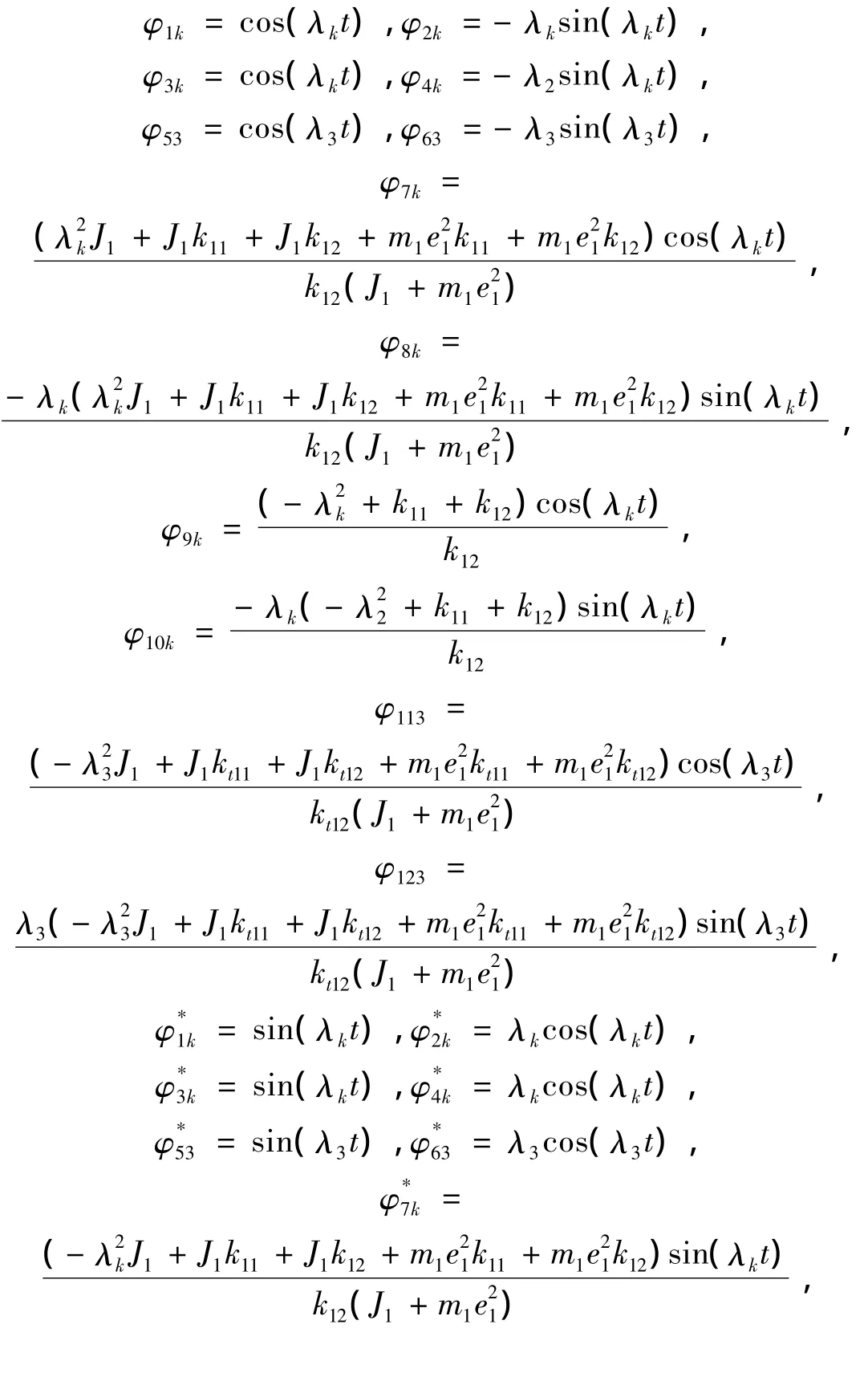
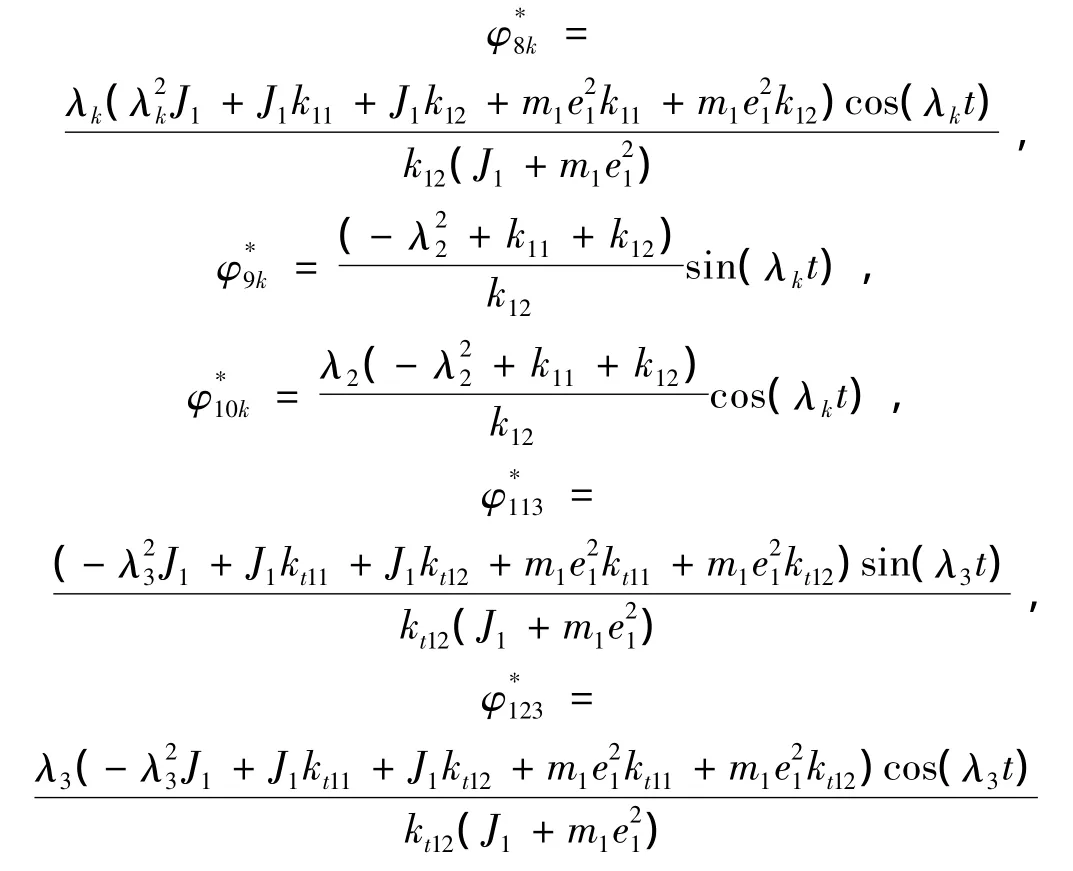
其中:φ是解的实部，φ*为解的虚部。

对方程(18)、(19)和(20)应用K－B变换

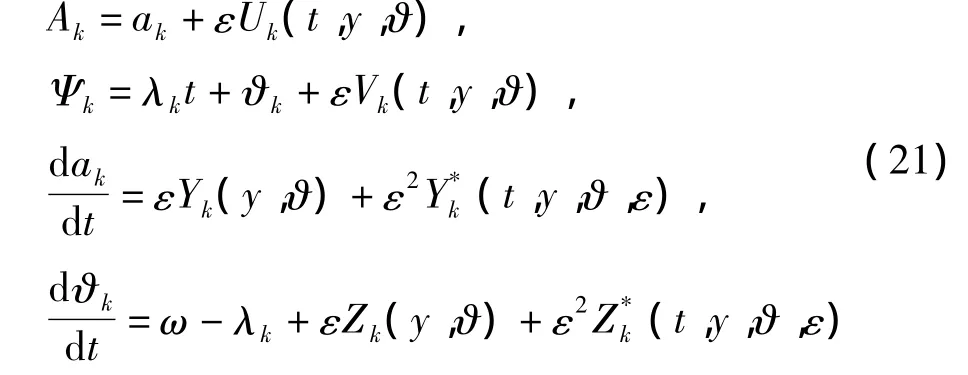
在次同步谐振的情况下，υ和λ3的关系如下:

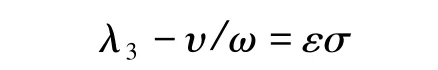
应用平均法，可以得到方程(23)的第一次近似解:

从方程(22)和(23)可以得到系统的分岔方程。

令 a3=x和2λ3－2υ/ω =λ，分岔方程转化为:

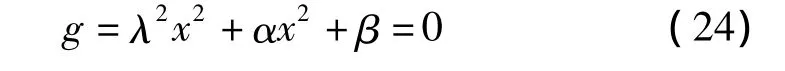
其中:λ是分岔参数，α和β是开折参数，它们是系统参数的组合。

根据奇异性理论[15]，可得系统的转迁集:

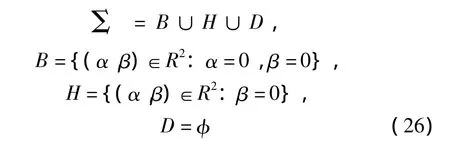
系统的转迁集和分岔图如图2所示。

图2 转迁集和分岔图Fig.2 The transition sets and bifurcation diagrams

从图2可以看出:转迁集将参数平面α－β分为4个不同的区间，在四个区间有四种不同的分岔模式。当α＞0，β＜0时为次同步谐振在转子扭转方向的振动;当α≥0，β≥0时，没有振动响应，也就是说在这个区间没有周期解;在α＜0，β＜0时，在共振区间振幅无穷大，在非共振区间振幅相对较小，参数尽量避免选在共振区间;当α＜0，β＞0振幅为无穷大，系统参数不能选在该区间。在转迁集上，有两种不稳定的分岔行为，α＜0，β=0是区间α＜0，β＞0和区间α＜0，β＜0的之间的过渡;α=0，β＜0是区间α＞0，β＜0和区间α＜0，β＜0分岔模式的过渡。对于实际的低压缸发电机转子系统，仅能取到 α≥0，β≤0这个区间。当α＞0，β=0时，为没有受到电网对机组的次同步谐振情况;当 α＞0，β＜0时，为系统受到次同步谐振影响引起的振动模式。

3 数值分析

采用4阶龙格库塔法对非线性方程(6)进行数值分析，系统的参数选择如下:

发电机和低压缸的在不同方向上的响应曲线如图3和图4所示。

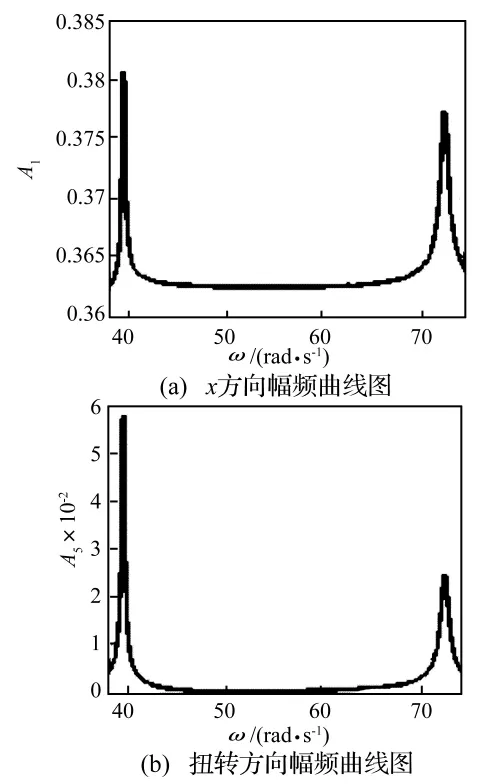
图3 发电机幅频曲线图Fig.3 Amplitude-frequency curves of generator

从选择的系统参数可以推出:

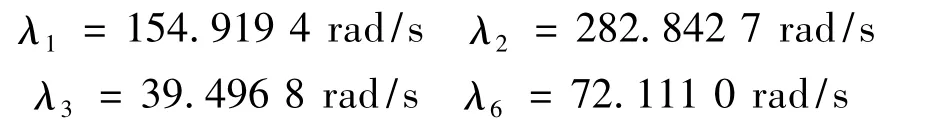
从图3和图4可以看出:次同步频率在扭转固有频率附近时，扭转振动的振幅大幅度增加。此外，由于偏心量引起的弯扭耦合现象的存在，在扭转振动振幅增加的同时，弯曲振动的振幅也随之增加。从图3、图4和相应的计算结果可以得出:在扭转固有频率附近，考虑弯扭耦合振动比不考虑弯扭耦合振动弯曲振动的振幅增加了 5.22个百分点(即5.22%，其中:A(f1)为考虑弯扭耦合振动弯曲振动的最大幅值，A(f2)为仅考虑弯曲振动弯曲振动的幅值)。在已经发表的次同步谐振文献中，研究轴系振动问题多集中在扭转振动方面。从上面的分析中可以得出:在次同步谐振机电扭转相互作用情况下，扭转振动的振幅变化比较明显，在扭转方向的危害极大，弯曲振动的振幅也有相应的变化。扭转的大幅度变化会引起弯曲方向振幅的增加，从而增加了弯曲方向破坏的可能性。因此在次同步谐振的情况下，仅考虑扭转是不全面的，应该将弯曲振动和扭转振动同时考虑。另外将数值结果和解析结果比较发现:数值结果的振动模式对应于转迁集中α＞0，β＜0区间内的分岔模式。此结果可为该系统设计和参数选择提供理论依据。

图4 低压缸幅频曲线图Fig.4 Amplitude-frequency curves of low pressure cylinder

4 结论

本文对低压缸和发电机转子轴系的弯扭耦合振动问题进行了研究，得到以下结论:

(1)偏心是引起弯扭耦合的原因，偏心量越大弯扭耦合越剧烈。应尽量减小偏心，从而降低弯扭耦合的作用效果。

(2)在次同步谐振的情况下，扭转振动的振幅变化比较明显，在扭转方向的危害极大，弯曲振动的振幅也有相应的变化。扭转的大幅度变化会引起弯曲方向振幅的增加，从而增加了弯曲方向破坏的可能性。因此在次同步谐振的情况下，仅考虑扭转振动是不全面的，应该将弯曲振动和扭转振动同时考虑更为合理。

(3)应用奇异性理论得到了系统的转迁集，在不同的参数区域内有不同的分岔模式。有些分岔模式可能会引起系统的破坏，因此在系统的设计阶段应尽量避开这样的参数区域。这为系统设计和参数选择提供理论基础。

[1]Al-Hussain K M，Rendmond I.Dynamic response of two rotors connected by rigid mechanical coupling with parallel misalignment[J].Journal of Sound and Vibration，2002，249(3):483－498.

[2]Al-Hussain K M.Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment[J].Journal of Sound and Vibration，2003，266:217 －234.

[3]Papadopoulos C A，Dimarogonas P A D，Louis St.Coupling of bending and torsional vibration of a cracked Timoshenko shaft[J].Ingenieur-Archiv，1987，57:257 －266.

[4]Papadopoulos C A，Dimarogonas A D.Coupled longitudinal and bending vinrations of s rotating shaft with an open crack[J].Journal of Sound and Vibration，1987，117(1):81－93.

[5]刘占生，崔 颖，黄文虎，等.转子弯扭耦合振动非线性动力学特性研究[J].中国机械工程学报，2003，14(7):603－605.

[6]IEEE subsynchronous resonance task force of the dynamic system performance working group power system engineering committee.First benchmark model for computer simulation of subsynchronous resonance[J].IEEE Transactions on Power Apparatus and Systems，1977(965):1565 －1572.

[7]IEEE subsynchronous resonance task force of the dynamic system performance working group，power system engineering committee.Second benchmark model for computer simulation of subsynchronous resonance[J].IEEE Transactions on Power Apparatus and Systems，1985(1045):1057 －1066.

[8]向 玲，唐贵基，朱永利.汽轮发电机组次同步谐振的数字仿真分析[J].华北电力大学学报，2005，32(2):32－36.

[9]向 玲，唐贵基，朱永利.汽轮发电机组次同步谐振及轴系扭振试验研究[J].华北电力大学学报，2005，32(4):85－87.

[10]向 玲，唐贵基，朱永利.300 MW汽轮发电机组在机电耦合作用下的扭振[J].动力工程，2007，27(4):492－496.

[11]刘 超，蒋东翔，谢小荣，等.次同步振荡引起的发电机组轴系疲劳损伤[J].电力系统自动化，2010，34(12):19－22.

[12]周 桐，徐健学，傅卫平.弯扭耦合振动对次同步谐振响应的影响[J].应用力学学报，2000，17(1):12－17.

[13]向 玲，杨世锡，唐贵基.次同步谐振下机组轴系弯扭振动信号分析[J].振动、测试与诊断，2011，31(2):233－236.

[14]Chen Y S.Nonlinear vibrations[M].Beijing:Higher Education Press，2002.

[15]Chen Y S，Andrew Y T.Leung bifurcation and chaos in engineering[M].London:Springer，1998.