双闭室复合材料薄壁梁的结构阻尼细观分析
2012-09-15任勇生宋玉壁孙双双
任勇生,宋玉壁,孙双双
(1.山东科技大学 机械电子工程学院,青岛 266510;2.青岛科技大学,青岛 266061)
在过去的几年间,风力发电机的尺寸持续增加,直径超过120 m的风轮样机正在样机试验阶段。随着风轮叶片尺寸的增加以及碳纤维复合材料的使用,在周围风场的作用下,不可避免地存在气动力、惯性力和弹性力间的耦合,有可能诱发叶片模态之间的耦合振动,导致叶片发生颤振。近来,关于风力机叶片颤振抑制,已经成为现代大型风力机结构动力学研究的一个重要的方面,日益受到风能工程领域的关注与重视[1-3]。
叶片颤振抑制可以采用主动与被动的方法。目前由于主动颤振抑制存在附加控制系统重量与能耗问题,特别是主动控制系统花费过大,势必增加风力发电的成本,因此,被动控制方法开始受到关注[2-3]。研究表明,被动阻尼在改善柔性结构的动力学特性,包括实施有效振动控制、提高疲劳寿命和改善气动弹性稳定性等方面,已经显示出较强的实用性。气弹阻尼作为气动阻尼和结构阻尼的总和,是衡量与控制叶片是否发生颤振的一个基本指标。树脂基纤维复合材料结构由于高分子材料内部晶体的内摩擦以及纤维/基体间的中间相阻尼,展示出高结构阻尼特性。此外,复合材料阻尼还能够通过提高组分阻尼、纤维混杂以及设置阻尼层进行调整,以获得理想的被动阻尼效果。复合材料结构阻尼的预测,离不开先进复合材料阻尼理论的指导。近年来,宏/细观阻尼分析理论在复合材料壳、板和实心梁的阻尼研究和设计以及复合材料结构的被动振动控制中,得到了广泛的应用[4],然而对风力机叶片这种复合材料结构阻尼特性的研究,至今尚不多见。风力机叶片具有闭合截面复合材料薄壁梁的结构特点,它不仅在风力机叶片上采用,在先进飞机固定机翼和直升机旋翼上也被使用。因此,建立闭合截面复合材料薄壁梁的结构阻尼分析模型,对于评价此类典型复合材料结构的阻尼耗散能力并且据此进行精确结构阻尼设计,以便于建立相应的被动颤振抑制有效方法,具有理论研究价值和工程实用性。
Suresh等[5]在不考虑复合材料薄壁箱形梁的结构特点以及截面翘曲变形情况下,采用经典的层合薄板有限单元法进行结构离散,复合材料的阻尼机理采用弹性-黏弹性对应原理(复模量法)进行描述,分析了边界条件和铺层角对固有频率和结构阻尼的影响。Saravanos等[6]从空心截面复合材料薄壁梁的几何和变形特征出发,基于Rehfied薄壳位移场方程[7],提出了一个管状层合复合材料梁的三维有限元阻尼分析模型,其中,复合材料阻尼通过耗散能进行度量,不计薄壁梁拉-剪耦合、拉-扭耦合和弯-扭弹性耦合的作用,得到三种规则截面梁阻尼分析结果。Chortis等[8]在Saravanos等[6]工作的基础上进一步研究了复合材料弹性耦合的影响,采用有限元方法计算了单/双闭室两种翼型截面的复合材料薄壁梁的模态阻尼,并对照实验结果进行了验证。Ramkumar等[9]分别采用三维梁和层合薄板两种有限元模型,研究薄壁复合材料箱形梁的阻尼特性。结构建模同样也是基于Rehfied薄壁梁理论,而复合材料阻尼的描述则采用复模量法并且不考虑薄壁梁扭转翘曲的影响。由于上述阻尼模型所依据的Rehfield薄壁梁理论非渐进准确,难以保证横截面刚度特性计算结果一致精确性[10]。
目前关于闭合截面复合材料薄壁梁的阻尼预测模型,仅限于有限元分析模型。虽然有限元离散在复杂结构的力学建模已经得到广泛的应用,但是由于计算量大、内存需求高,对于此类结构的阻尼预测,缺乏实用性。任勇生等[11]基于复合材料薄壁梁理论并且结合最大应变能理论,建立了弯扭耦合复合材料单闭室薄壁梁的结构宏观阻尼预测的分布参数模型,采用Galerkin法求解振动分析模型,分析了纤维铺层角、薄壁梁长宽比和截面宽高比对阻尼性能的影响。计算过程表明,基于上述分布参数模型,具有计算速度快和内存需求小的优点,并且所得到的计算结果与有限元相比可以满足对计算精度的要求。
单闭室与双闭室截面梁的主要差别表现在对扭转的分析,由于双闭室截面梁属于静不定问题,存在无法由平衡方程确定的独立的剪力流,特别是对于各向异性复合材料梁而言,由于扭转与其它变形之间的耦合,上述差别变得更为明显,因此,双闭室复合材料薄壁梁的横截面剪切与扭转特性分析相对具有较大的难度。
本文在前期研究的基础上,提出一个弯扭耦合复合材料双闭室薄壁梁的结构阻尼连续分布模型。基于单层混杂材料的细观力学阻尼计算方法[12]和多胞模型[13],分别获得单层复合材料的等效阻尼特性和等效弹性特性,薄壁梁采用VAM[10]进行结构力学建模,基于Hamilton原理导出复合材料薄壁梁的自由振动模型,将位移按广义坐标进行模态展开,采用Galerkin法求解振动分析模型。在导出复合材料薄壁梁的应变能和耗散能表达式的基础上,根据最大应变能理论,对双闭室薄壁复合材料梁模态阻尼性能进行理论分析,双闭室截面刚度系数采用文献[14]给出的公式进行计算,通过数值近似计算,揭示了纤维含量、纤维铺层角对阻尼性能的影响。
1 分析模型
1.1 位移场和应变场
本节采用VAM[10]导出各向异性双闭室薄壁截面梁的位移场和二维截面分析模型。图1表示一细长的双闭室复合材料薄壁梁,长度为L,厚度h,中面曲率半径 r,d表示最大横截面尺寸。假定 d≪L,h≪d,h≪r,坐标ξ沿中面法线方向度量,满足 -h/2≤ξ≤h/2。(x,y,z)表示薄壁梁整体坐标系;(x,s,ξ)表示薄壁梁局部坐标系,s沿截面中线(即,薄壁梁的中面与横截面的交线)切向,ξ沿截面中线外法线方向。
薄壁梁上的任意点沿坐标系(x,y,z)的三个坐标轴方向的位移分量为[10]:

其中:截面翘曲函数g(s,x)由位移场的连续性、环向力为零以及定常剪力的条件决定。
与位移场(1)相对应的二阶近似应变场为:
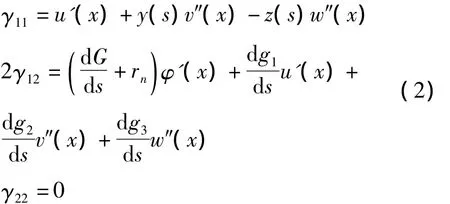

图1 双闭室坐标系统及运动学变量图Fig.1 Two-cell coordinate systems and kinematic variables
1.2 复合材料薄壁梁的应变能密度
复合材料薄壁梁的应变能密度:
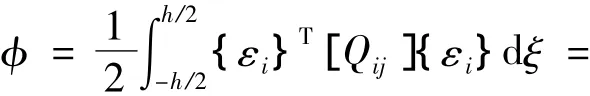
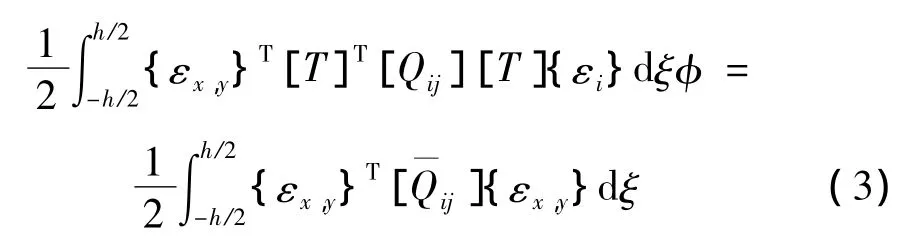
对式(3)沿厚度积分,可得:

其中:

hk、hk-1分别为第k层的上、下表面坐标,N 为总层数。
假设薄壁梁的环向应力很小,可以忽略不计,则有:

由式(4)、(6),得:
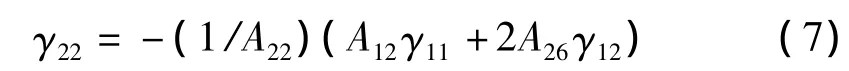
将式(7)代入(4)消去 γ22,得:
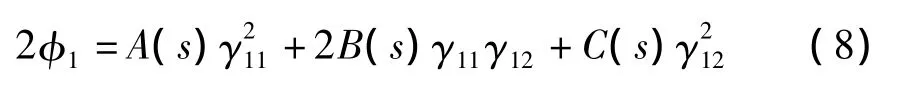
其中:
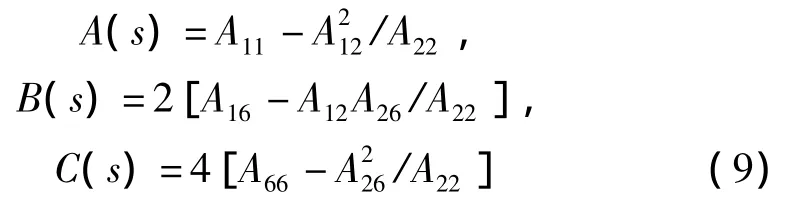
复合材料薄壁梁的应变能为:

利用应变-位移关系(2),得位移/扭转角表示应变能为:

1.3 复合材料薄壁梁的耗散能密度
复合材料薄壁梁的耗散(阻尼)应变能密度:

其中:阻尼(损耗因子)矩阵[ψ]为下列对角矩阵:
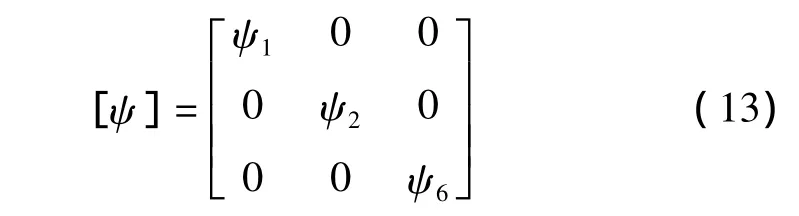
其中:ψ1,ψ2,ψ6分别表示纤维复合材料单层的轴向、横向拉压和面内剪切损耗因子。
假设:① 基体/纤维界面相互不脱离,为理想粘结;② 复合材料各组分的应变沿纤维方向是相等的,材料应力在与纤维垂直方向是均匀的;③ 纤维与基体具有粘弹性性质,且纤维单向埋设。于是按照复合材料细观力学阻尼分析理论,由纤维和基体构成的复合材料介质,其阻尼性能可直接由下式计算[12]:

其中:下标n,s分别表示拉压和剪切方向,m表示基体,Vf表示纤维含量。
复合材料介质的宏观弹性常数采用多胞模型计算如下[13]:
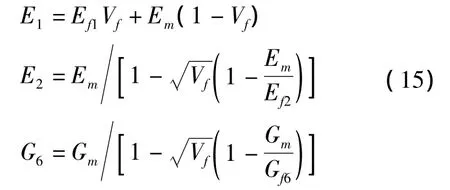
一般来说,矩阵(13)中的元素ψi是材料内部应力幅值的函数,但是在理想的线性阻尼分析的框架下,可以近似地认为ψi与应力幅值无关,于是迟滞环的形状为椭圆形,ψi具有定常的特性。
由式(12)积分得:

其中:

类似地,利用式(7)对式(19)进行简化,得:

其中:
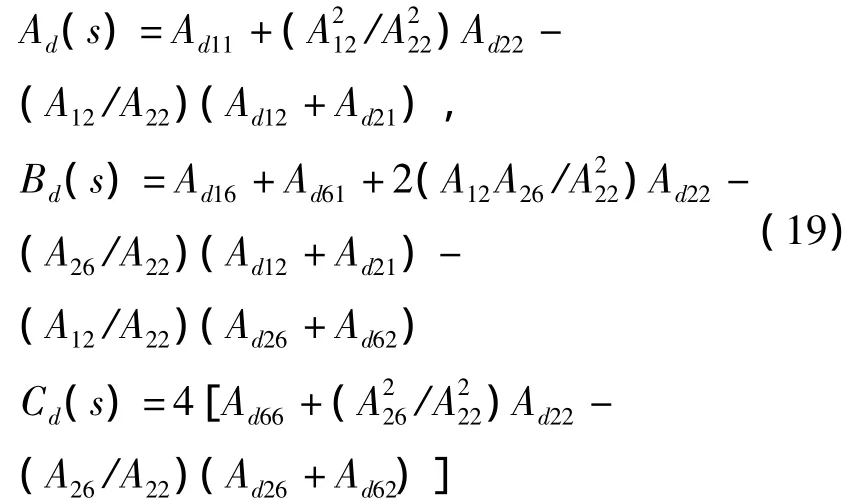
复合材料薄壁梁的耗散能为:
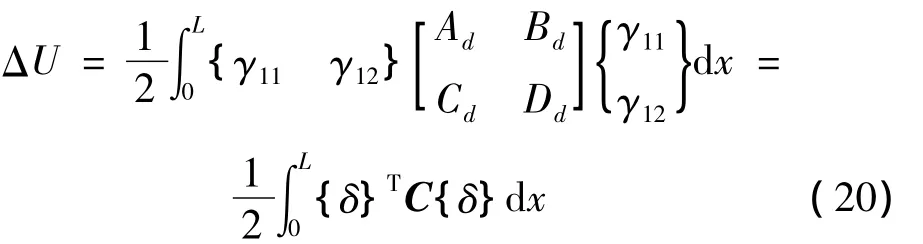
其中:C为复合材料薄壁梁横截面的4×4阻尼矩阵,其矩阵元素表达式类似于刚度矩阵K,只需要将A(s),B(s),C(s)替换为 Ad(s),Bd(s),Cd(s)即可得到。
1.4 复合材料薄壁梁的自由振动方程及其求解
为了导出复合材料薄壁梁的运动方程,利用Hamilton原理:
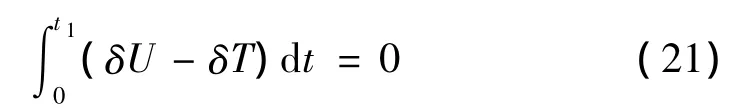
其中:动能T可由下式确定:
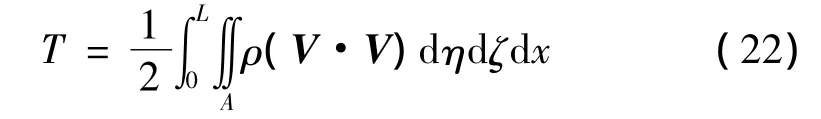
ρ为材料密度,V表示变形后的梁上任意一点的速度矢量,它与变形梁任意一点的位置矢量:r=(x+u1)i之间满足关系:表示对时间t求偏导。
由Hamilton方程(21),可导出复合材料薄壁梁的无阻尼自由振动偏微分方程组[15]。采用Galerkin法可进一步导出复合材料薄壁梁的自由振动问题的特征方程:

其中:

{Xm}是复合材料薄壁梁的模态矢量。
1.5 结构阻尼
复合材料薄壁梁的模态阻尼比可以定义为每个振动周期内的耗散(阻尼)能与最大应变能之比:
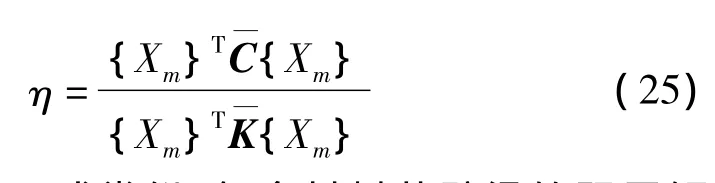
与式(24)中的第一式类似,复合材料薄壁梁的阻尼矩阵C—具有下列形式:
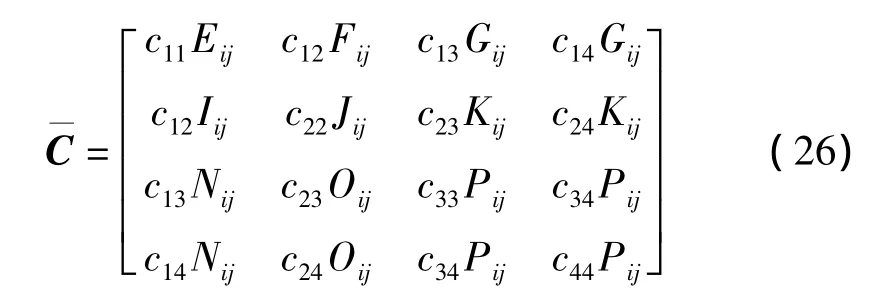
2 结果及讨论
首先,为了验证双闭室复合材料箱形薄壁梁刚度系数结果的正确性,表1给出了如图3所示构型,即沿薄壁梁截面的周线的铺层方室分别为[+45]2和[-45]2,双闭室复合材料箱形薄壁梁的刚度系数计算结果,并且与文献[16]及[17]的结果进行了比较,模型的几何参数和材料参数均取自两篇文章。可以看出,三者的计算结果较吻合。
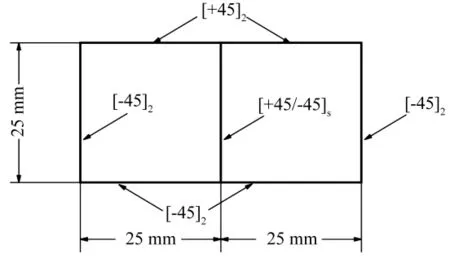
图2 双闭室箱型薄壁梁截面Fig.2 Two-cell thin-walled box beam cross section
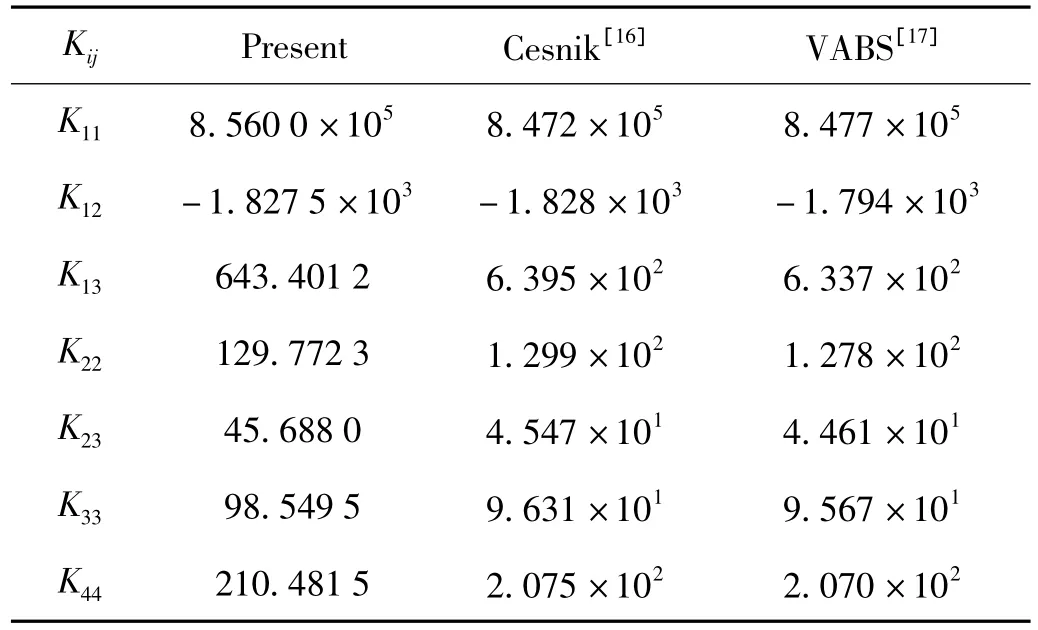
表1 双闭室复合材料箱形薄壁梁的刚度系数计算结果Tab.1 Stiffiness results for two-cell beam.
其次,为了检验本文建立的复合材料薄壁梁阻尼模型及其近似计算方法的正确性,表2、表3给出在两种CUS构型,即沿薄壁梁截面的周线的铺层方式分别为[0]16和[90]16,复合材料箱型截面薄壁悬臂梁的模态阻尼和固有频率计算结果,并且与文献[6]的3D剪切梁阻尼有限元结果进行了比较,结构的几何参数和材料参数均取自文献[6]。可以看出,二者符合得很好。
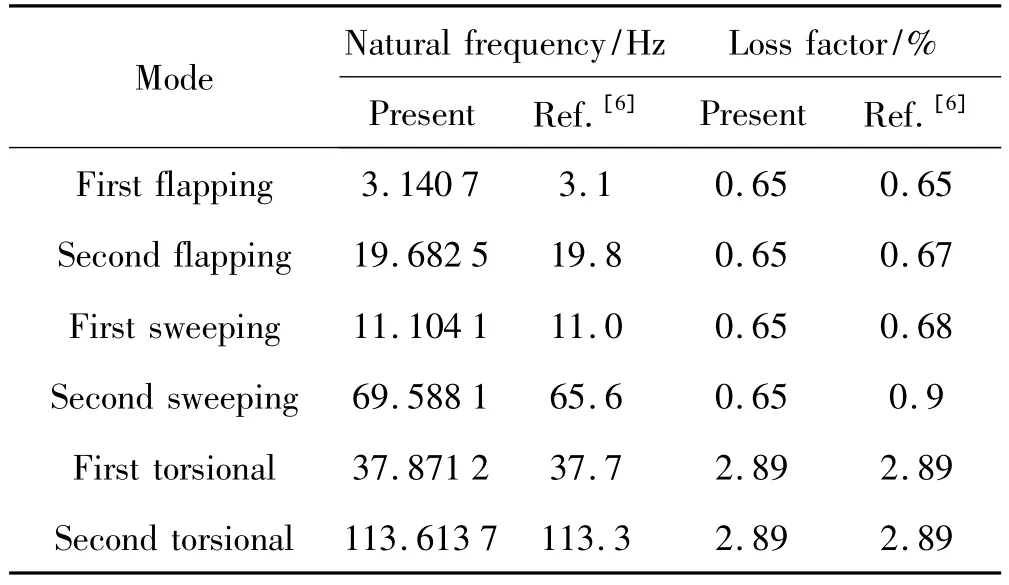
表2 复合材料箱形梁的模态频率和阻尼,L/a=14.36,a/b=5,[0]16Tab.2 Modal frequency and damping of cantilever composite

表3 复合材料箱形梁的模态频率和阻尼,L/a=14.36,a/b=5,[90]16.Tab.3 Modal frequency and damping of cantilever composite
下面分别计算图3所示四种构型下双闭室复合材料薄壁梁的结构阻尼。模型的几何尺寸为:外截面宽度 a=0.025 m,外截面高度 b=0.025 m,长度 L=1.524 m,单层厚度0.000 127 m,铺层数为6 层,复合材料基体与纤维性能参数如表4所示。双闭室箱形复合材料薄壁梁结构如图3所示。

表4 复合材料性能参数Tab.4 Mechanical properties of composite material

图3 双闭室箱型梁模型Fig.3 The diagram of double-cell thin-walled box beam
图4 表示具有图3(a)构形的双闭室复合材料薄壁悬臂梁的第一阶弯曲为主模态阻尼随铺层角的变化曲线,其中也显示出纤维含量的影响。结果表明,弯曲为主模态阻尼随着铺层角的增加呈现先增加后减少的变化趋势,最大阻尼发生在铺层角θ为50°附近,在铺层角90°的阻尼大约是0°阻尼值的5倍左右。增加纤维含量,可以在一定的铺层角范围内提高或者降低薄壁梁的阻尼,但是这种作用的效果并非很明显。图5表示具有图3(a)构形的双闭室复合材料薄壁悬臂梁的第一阶扭转为主模态阻尼随铺层角的变化曲线。显然,扭转为主模态阻尼随着铺层角的变化趋势,与弯曲为主模态阻尼是相反的,最小阻尼发生在35°~55°之间,铺层角90°的阻尼大和0°阻尼值是相同的。铺层角在0°~90°之间,增加纤维含量可以明显提高阻尼值。
图6表示具有图3(b)构形的双闭室复合材料薄壁悬臂梁的第一阶挥舞弯曲模态阻尼随铺层角的变化曲线,结果表明,阻尼随铺层角的变化规律与具有图3(a)构形的双闭室的结果(见图4)是类似的。图7表示具有图3(b)构形的双闭室复合材料薄壁悬臂梁的扭转-挥舞弯曲耦合模态阻尼随铺层角的变化曲线,阻尼随铺层角的变化以及纤维含量的影响,与具有图3(a)构形的双闭室情形下的结果(见图5)是类似的。
图8和图10分别表示对应于图3(c)和3(d)构形的双闭室复合材料薄壁悬臂梁的第一阶挥舞弯曲模态阻尼随铺层角的变化曲线,结果表明,阻尼随铺层角的变化规律与具有图3(a)构形的双闭室的结果(见图4)是类似的。图9和图11分别表示对应于图3(c)和3(d)构形的双闭室复合材料薄壁悬臂梁的扭转-挥舞弯曲耦合模态阻尼随铺层角的变化曲线,阻尼随铺层角的变化以及纤维含量的影响,与具有图3(a)构形的双闭室情形下的结果(见图5)是类似的。
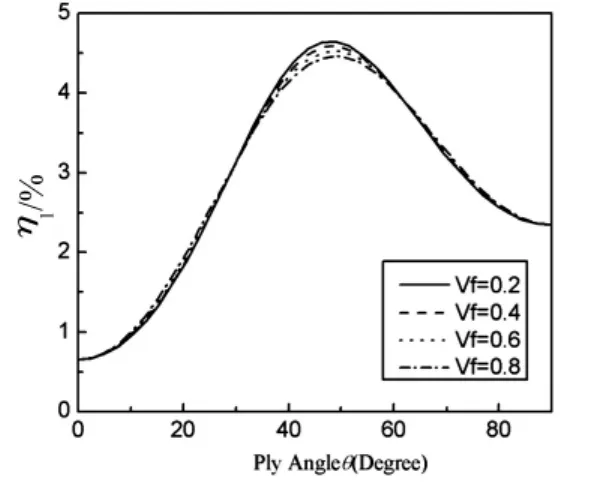
图4 不同纤维含量的薄壁梁(图3(a))的第一阶弯曲为主模态阻尼随铺层角变化曲线Fig.4 The first bending modal damping for the beam(Fig.3 (a))vs.ply angle for various fibre volume fraction
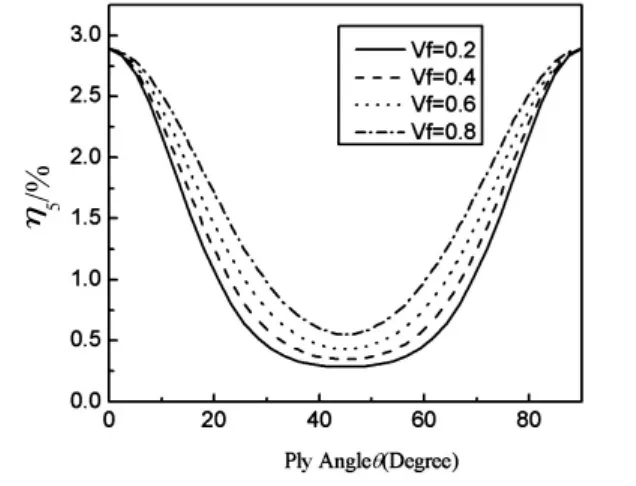
图5 不同纤维含量的薄壁梁(图3(a))薄壁梁的第一阶扭转为主模态阻尼随铺层角变化曲线Fig.5 The first twisting modal damping for the beam(Fig.3 (a))vs.ply angle for various fibre volume fraction
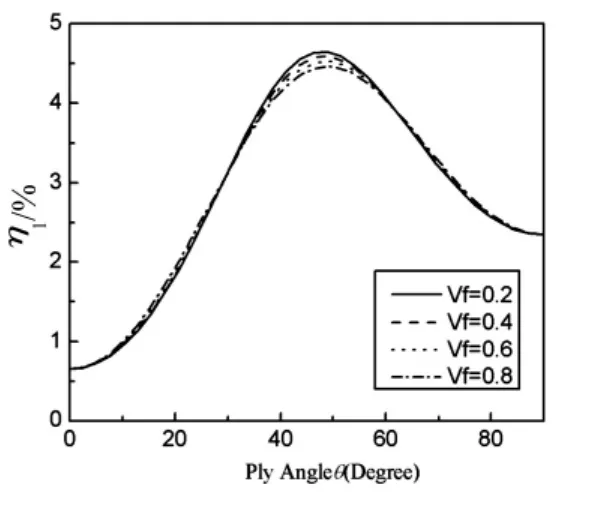
图6 不同纤维含量的薄壁梁(图3(b))的第一阶弯曲为主模态阻尼随铺层角变化曲线Fig.6 The first bending modal damping for the beam(Fig.3 (b))vs.ply angle for various fibre volume fraction
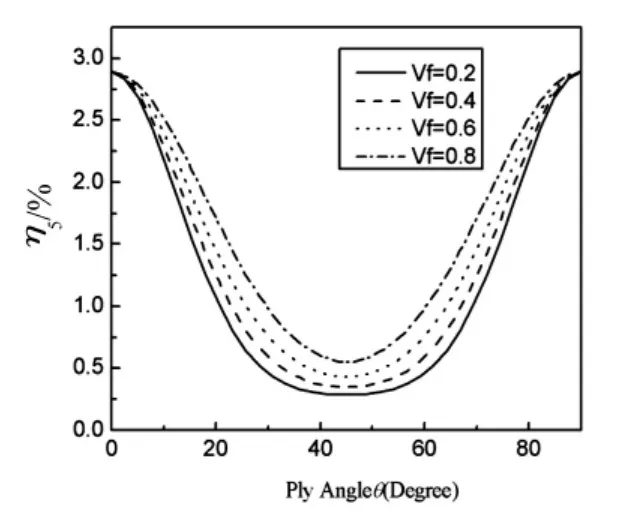
图7 不同纤维含量的薄壁梁(图3(b))薄壁梁的第一阶扭转为主模态阻尼随铺层角变化曲线Fig.7 The first twisting modal damping for the beam(Fig.3 (b))vs.ply angle for various fibre volume fraction

图8 不同纤维含量的薄壁梁(图3(c))的第一阶弯曲为主模态阻尼随铺层角变化曲线Fig.8 The first bending modal damping for the beam(Fig.3 (c))vs.ply angle for various fibre volume fraction
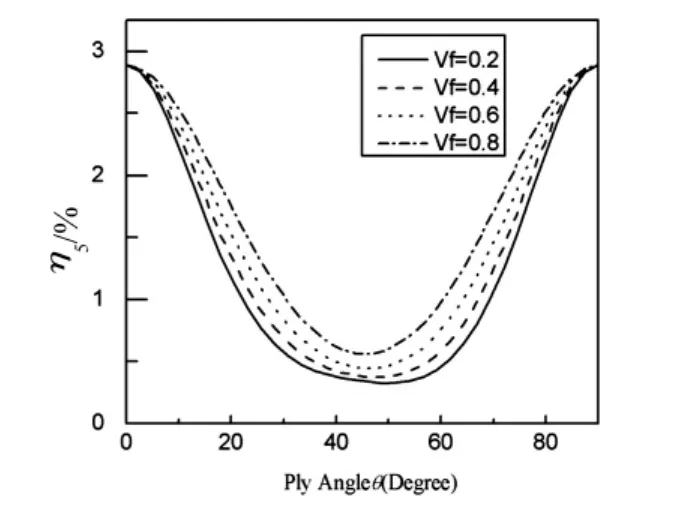
图9 不同纤维含量的薄壁梁(图3(c))薄壁梁的第一阶扭转为主模态阻尼随铺层角变化曲线Fig.9 The first twisting modal damping for the beam(Fig.3 (c))vs.ply angle for various fibre volume fraction

图10 不同纤维含量的薄壁梁(图3(d))的第一阶弯曲为主模态阻尼随铺层角变化曲线Fig.10 The first bending modal damping for the beam(Fig.3 (d))vs.ply angle for various fibre volume fraction
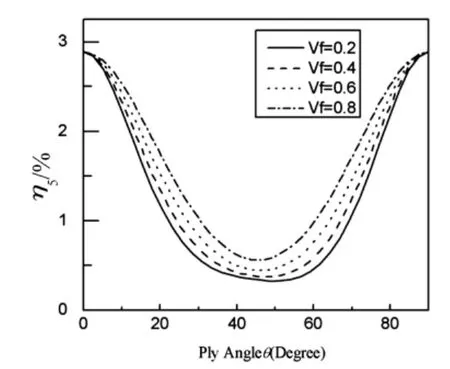
图11 不同纤维含量的薄壁梁(图3(d))薄壁梁的第一阶扭转为主模态阻尼随铺层角变化曲线Fig.11 The first twisting modal damping for the beam(Fig.3 (d))vs.ply angle for various fibre volume fraction
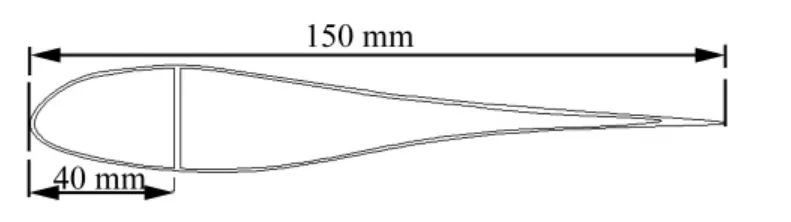
图12 双闭室风力机叶片截面翼型轮廓线Fig.12 Two cell airfoil profile composite beam
图12 给出一个带有腹板的双闭室风力机叶片翼型轮廓线,它由文献[19]翼型曲线的计算公式画出。翼型轮廓线以及腹板的铺层方式取[θ]6。梁长为0.762 m,复合材料性能参数取自表4。图13和14分别表示纤维含量以及铺层角对第一阶挥舞弯曲模态阻尼和第一阶扭转-挥舞耦合模态阻尼的影响规律,可以看出,在上述铺层方式下,铺层角的影响与双闭室箱型截面梁的结果是相似的,但是纤维含量的影响与双闭室箱型截面梁的结果有所不同。
3 结论
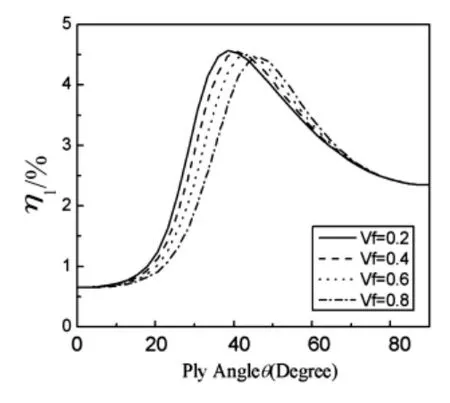
图13 双闭室翼型截面复合材料薄壁梁的第一阶弯曲为主模态阻尼随铺层角变化曲线Fig.13 The first bending modal damping for the beam vs.ply angle for various fibre volume fraction

图14 双闭室翼型截面复合材料薄壁梁的第一阶扭转为主模态阻尼随铺层角变化曲线Fig.14 The first twisting modal damping for the beam vs.ply angle for various fibre volume fraction
本文基于单层混杂材料的细观力学阻尼计算方法和多胞模型,综合采用VAM法和Hamilton原理并且借助于Galerkin法,建立了弯扭耦合复合材料双闭室薄壁梁的结构阻尼分析模型。研究结果表明,采用本文建立的解析模型及其近似计算方法所获得的薄壁箱形悬臂梁的模态阻尼与固有振动频率数值近似解,与已有文献的有限元解相当一致。双闭室薄壁复合材料梁的结果阻尼的分析结果表明:
(1)根据本文模型能够对双闭室薄壁复合材料梁的结构阻尼性能进行参数分析,以确定影响薄壁梁阻尼性能的主要因素,为进一步改善或提高薄壁梁的阻尼耗散性能,提供有用的信息。
(2)纤维铺层角对薄壁梁的结构阻尼能够产生明显的影响。对于弯曲为主模态来说,相应的阻尼最大值出现在50°铺层角附近;对于扭转为主模态,相应的阻尼最小值出现在35°~55°铺层角附近,并且在上述两种情形下阻尼随纤维铺层角的变化规律是相反的。
(3)随着纤维含量的增加,可以在一定的铺层角范围内提高或者降低薄壁梁弯曲为主和扭转为主振动模态的结构阻尼,纤维含量的影响效果将取决于双闭室薄壁复合材料梁的截面的铺层方式以及构型。
[1]Barlas T K,Van Kuik G A M.Review of state of the art in smart rotor control research for wind turbines[J].Progress in Aerospace Sciences,2010,46(1):1 -27.
[2]Hansen M H Aeroelastic instability problems for wind turbines[J].Wind Energy,2007,10:551 -577.
[3]Chaviaropoulos P K,Politis E S,Lekou D J,et al.Enhancing the damping of wind turbine rotor blades,the DAMBLADE Project[J].Wind Energy,2006,9:163 -177.
[4]任勇生,刘立厚.纤维增强复合材料结构阻尼研究进展[J].力学与实践,2004,26(1):9 -16.
[5]Suresh R,Malhotra S K.Vibration and damping analysis of thin-walled box beams[J].Journal of Sound and Vibration,1998,215(2):201-210.
[6]Saravanos D A,Varelis D,Plagianakos T S,et al.A shear beam finite element for the damping analysis of tubular laminated composite beams[J].Journal of Sound and Vibration,2006,291:802 823.
[7]Rehfield R W.Design analysis methodology for composite rotor blades[C].Proceedings of the Seventh DoD/NASA Conference on Fibrous Composites in Structural Design.Denver,CO,Grant NAG-2-238,1985.
[8]Chortis D I,Chrysochoidis N A,Saravanos D A.Damped structural dynamics models of large wind-turbine blades including material and structural damping[J].Journal of Physics:Conference Series,2007,75:1 -11.(doi:10.1088/1742-6596/75/1/012076).
[9]Ramkumar K,Ganesan N,Kannan R.Global and local behaviour based composite damping studies on thin-walled box structure[J].European Journal of Mechanics A/Solids,2010,29:253-265.
[10]Berdichevsky V L,Armanios E,Badir A M.Theory of anisotropic thin-walled closed-cross-section beams[J].Composites Engineering,1992,2(5 -7):411 -432.
[11]任勇生,杜向红,孙双双,等.单闭室复合材料薄壁梁的结构阻尼[J].振动与冲击,2012,21(3):141-146.
[12]Saravanos D A,Chamis C C.Unified micromechanics of damping for unidirection and off-axis fiber composites[J].J CompositesTechnology & Research. JCTRER, 1990,12(1):31-40.
[13]Murthy P L N. Second generation integrated composite analyzer(ICAN)computer code[R].NASA TP 3290,1993.
[14]Badir A M.Analysis of two-cell composite beams[C].Proceedings of the 36th AIAA Structures,Structural Dynamics and Materials Conferences,New Orleans,AIAA 95-1208 -CP,1995.
[15]任勇生,杜向红,杨树莲.风力机复合材料柔性叶片的颤振分析[J].振动与冲击,2011,30(9):64-69,128.
[16]Cesnik C E S,Shin S J.On the modeling of integrally actuated helicopter blades[J].International Journal of Solids and Structures,2001,38:1765-1789.
[17]Cesnik C E S,Hodges D H.VABS:A new concept for composite rotor blade cross-sectional modeling[J].Journal of American Helicopter Society,1997,42(1):27 -38.
[18]Kaliske M, Rothert H. Damping characterization of unidirectional fiberreinforced polymercomposites[J].Composites Engineering,1995,5(5):551 -567.
[19]王旭东,陈 进,Shen W Z,等.风力机叶片翼型型线集成设计理论研究[J].中国机械工程,2009,20(2):211-213,228.
附录:刚度系数的求解[14]
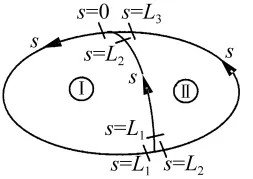
图15 双闭式截面Fig.15 Schematic of two-cell section
如图15所示,双闭式截面被分成了三部分。位移场中提到的一些系数可以通过图15每个部分求解:
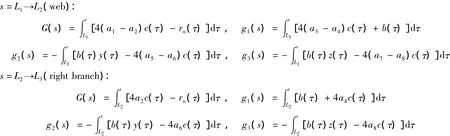
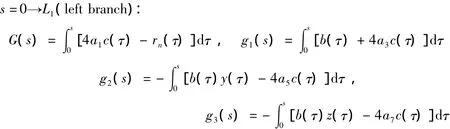
其中:

下标Ⅰ和Ⅱ表示图中的左右两个闭室。分别用AeⅠ和AeⅡ表示下标为Ⅰ和Ⅱ的左右两个闭室的面积。刚度矩阵[K]是4×4对称阵,其中的元素组成Kij( i,j=1,2,3,4)由横截面的几何变化和材料的性质决定,表达式为: