人体站姿竖向振动等效单自由度模型参数研究

杨 予，杨云芳，洪 震，胡杰云，蔡其茅

(浙江理工大学 建工学院 土木系，杭州 310018)

由于现代工程材料和技术的发展，现代都市中的建筑结构有轻量化发展趋势，近年来建筑物中的人与结构耦合振动问题日益突出。在进行人与结构耦合振动分析时，常遇到的关键性问题是对人体进行合理的简化建模并给出适当的模型参数。

在人体动力学建模方面，目前已经积累有许多研究成果，代表性的研究者有 Subashi[1]，Matsumoto[2－3]，Wei[4]，Griffin[5]等，常见研究方法是视人体为多自由度模型，采用装有传感器的刚性电液伺服振动台，通过施加随机振动激励的方式测出不同频段人体站姿或坐姿情况下与结构的接触力或位移，然后根据实验数据识别各人体模型的各部分参数。另一方面，考虑到分析相对便捷，人体单自由度简化动力学模型在实际工程中仍有相当广泛的应用，但从一些公开发表的文献资料中不难发现，目前在模型参数取值上尚无统一标准，例如:何浩祥等在文献[6]中采用的人体竖向自振频率为3.84 Hz，Dougill在文献[7]中采用了 2.3 Hz的人体竖向自振频率和25%的阻尼比，陈建英等在文献[8]中给出的人体竖向自振频率为5.12 Hz，阻尼比为0.42，樊健生等在文献[9]中采用的人体竖向自振频率为 5.24，阻尼比为 0.39。

考虑到单自由度简化模型参数取值对动力学分析结果的影响，很有必要对其进行更为深入的研究和探讨。本研究的目的是通过理论推导和实验测试手段得出人与结构作耦合自由振动时的等效单自由度简化模型参数，并讨论这些参数对结构参数和人体局部姿态的敏感性，为工程中的相关分析提供直观的取值依据。

1 人体一维简化理论

设当采用n(n＞1)自由度模型对人体进行描述时，人体与结构耦合振动的动力学特征可以满足所需精度要求，则此时对应的人体一维简化模型应为该多自由度模型的某一最佳数值逼近。为说明其原理，试考察图1中所示的两个耦合振动结构体系:

图1 等效振动体系分析Fig.1 Theory of equivalent vibration system

图1 (a)中一个两自由度串联弹簧－质量块系统(代表人体)放置于一单自由度弹簧－质量块系统上，构成耦合振动体系，设ks=k1=k2=k，ms=2m，m1=m2=m，如图1(a)所示。由结构动力学可知该系统的主振型与各子系统的弹簧刚度与质量取值有关，若设该体系的初始状态为{u0}=[1 1 1]T，{}=[0 00]T，则按振型分解法可求出质量ms的自由振动如式(1)所示:

现考虑将该两自由度串联弹簧－质量块体系等效化为单自由度模型，为便于工程应用，取新体系中的参数 Ks=k，Ms=ms，Mh=m1+m2，如图 1(b)所示，则等效化问题可归结为:求出新体系下的弹簧刚度Kh，使得相同初始条件下Ms的振动反应与原系统中ms的振动反应具有最佳近似性。

相应地，假定该系统初始状态为{U0}=[1 1]T，，则按振型分解法可求出质量 Ms的自由振动，如式(2)所示:

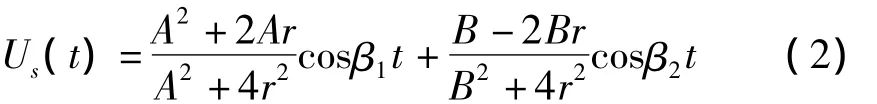
比较(1)、(2)两式右端可见，想要上述两个体系在任意t时刻的振动完全一致就必须让各项系数和频率值分别相等，而这显然是不可能的。因此，为使一维等效简化模型具有工程应用价值，可考虑按最小二乘法进行拟合，即作两者误差之平方对时间的积分函数F，如式(3)所示:

显然，若能够找到一个Kh值使得误差函数F在所需特定积分时间段T=t2－t1内取极小值，则此Kh值就是该时间段内所求的一维等效模型的最佳逼近参数。

推及一般情形，在考虑阻尼的作用时，式(3)可改为:

由此可见，本文中人体一维简化模型的具体物理意义为:寻找适当的人体刚度值 Kh和阻尼值Ch使得简化耦合振动体系结构振动反应与精确耦合振动体系结构振动反应的误差在某所需特定时间段T内最小。

此外，根据上述分析尚可有如下推论:当结构取不同动力学参数时，由于耦合振动体系的主振型将发生相应变化，人体的一维简化模型参数也随之改变。

2 实验测试与数据处理

根据上述等效原理，考虑到人体建模的复杂性，直接根据实验数据导出一维等效参数较合理。为便于对比验证，本文研究中利用两台不同原理的单自由度实验台进行测试，如图2所示，并采用Power1401数采系统和压电式加速度传感器等对实验台进行加速度数据采集，采样率为1 024 Hz。表1中列出了振动台和待测志愿者的参数，其中振动台一用于模拟自振频率较高、质量较轻的刚性结构，振动台二用于模拟自振频率较低、质量较重的柔性结构。

图2 实验采用的两种单自由度振动台Fig.2 Two SDOF test rig used in experimental study

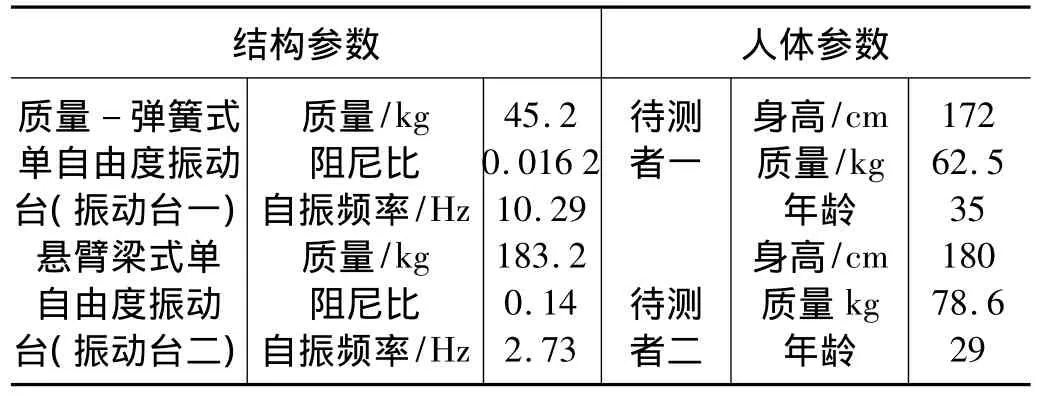
表1 人与结构耦合振动实验参数条件Tab.1 Parameters of human body and test rigs

在实验中采用赋予振动台一定位移的方法进行初始激励，为验证参数对人体局部姿态的敏感性，分别测试了双脚并拢自然直立、双脚尖踮起直立、双手向上直举、双脚尖踮起直立同时双手向上直举以及屈膝站立五种典型站立姿势情况下的振动台自由振动情况。

为避免出现不合理的结果，根据参考文献[1－4]中的人体特征参数识别情况，在拟合分析中取人体竖向自振频率和阻尼比的上下限值分别为0.1 Hz≤fh≤10 Hz，0≤ξh≤0.4，具体数据处理流程如下:

(1)取数据点P0，在P0处对采样数据加矩形窗截取激励完成后T=2 s时间段内的加速度向量[]，并对[进行规格化处理得到最大加速度为1的加速度向量[];(2)根据经验给定合理的迭代初始频率 fh0和初始阻尼 ξh0，将其与 Mh以及振动台振动参数代入式(5)，并令时间步长为1/N，采用数值积分方法对自由振动进行求解，得出各时间点加速度向量[];

(5)考虑到截取测试数据的偶然性，调整截断点P0位置作一维搜索，并重复步骤(1)－(4)，直至找到最小的二乘法误差函数值，则此时对应的即为所求的人体单自由度等效自振频率和阻尼比。

3 实验结果分析

图3(a)为刚性振动台一所测得的加速度时程曲线以及参数拟合曲线，作为对比，图3(b)中绘出了不考虑人体频率和阻尼，将人体视为单纯质量直接与实验台质量叠加作为单自由度振动体系的理论分析结果。由图3可见，按本文方法得出的人体单自由度简化模型与实验结果具有不错的拟合精度，在工程实用性上显然好于将人体单纯视为质量。

图4给出了刚性振动台一上五种典型站姿的等效参数分析结果(多次测试取平均值)，由图可知:① 刚性振动台上测试者的等效自振频率受站姿变化影响的相对幅度较小，而等效阻尼受站姿变化影响的相对幅度较大;② 一些人体局部姿态如举手、屈膝对测试者的等效自振频率无明显影响，但对等效阻尼比有较明显影响。

图5(a)为柔性振动台二所测得的加速度时程曲线以及拟合曲线，作为对比，图5(b)给出将人体集中质量与振动台质量直接叠加的单自由度体系理论分析结果。由图6可见，此时等效单自由度模型拟合误差较大，但仍好于将人体视为单纯质量的情形。

图3 振动台一:两种简化模型对比Fig.3 Comparison of two simplified models of human body on test rig 1

图4 振动台一:五种站姿自振参数Fig.4 Parameter identification of five standing postures on test rig 1

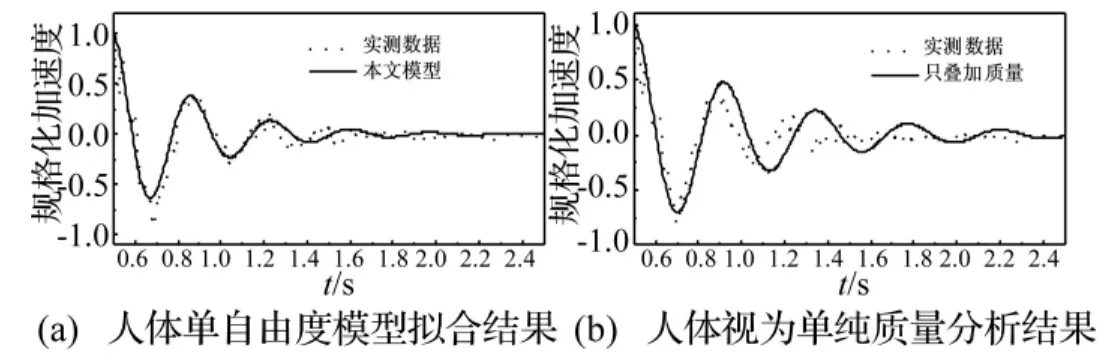
图5 振动台二:两种简化模型对比Fig.5 Comparison of two simplified models of human body on test rig 2

图6 振动台二:五种站姿自振参数Fig.6 Parameter identification of five standing postures on test rig 2

图6 给出了五种典型站姿的参数识别情况(多次测试取平均值)，观察图6可得出与图4类似的结论。但比较图6与图4可发现一些不同，即:① 柔性振动台上测试导出的人体等效自振频率(约2 Hz)要低于刚性振动台上的相应数值(约4.5～6 Hz)，约为后者的1/3～1/2;② 柔性振动台上测试导出的等效阻尼比(约0.3～0.4)远高于刚性振动台上的相应数值(约0.02～0.09)，最大差距可达到10倍以上。

综合理论分析和实验结果可知，若耦合振动体系的主振型参数发生变化，人体单自由度简化模型参数取值也将随之改变，但若站立的局部姿态变化不大可考虑忽略其影响。为便于工程应用，可根据实验分析统计结果绘制相关图表备查。

例如，图7是通过调整振动台参数对同一待测者进行测试，获得的两条简化模型参数曲线，由图7(a)可见，测试者等效自振频率随结构自振频率和质量比在5～10 Hz之间变化，而由图7(b)可见，测试者等效阻尼比也随结构自振频率和质量比在0.2～0.4之间变化。

图7 单自由度等效模型参数与结构参数关系Fig.7 Variation of equivalent human body parameters with structure parameters

4 结果验证与结论

本文实验中采用了初始位移激励后测量拟合自由振动加速度时程的方法，这与国内外相关研究中采用的根据电液伺服振动台扫频分析结果对人体模型进行参数识别的原理有所不同，但所得结果仍有一些相似之处:

(1)在刚性较大的振动台一上，两位测试者自然站立的等效自振频率分析结果在4.3～5.7 Hz范围内变化，这与Subashi，Matsumoto，Griffin等在电液伺服振动台上得出的人体直立时全身共振频率约为5～6 Hz的结论[1]接近;

(2)研究中发现测试者双手上举对于等效自振频率无明显影响，这也和Subashi，Matsumoto，Griffin等在实验中发现上肢姿态对人体共振频率无明显影响[1]一致;

(3)相似条件下，研究中得出的人体等效阻尼比波动范围(0.2～0.4)与 Matsumoto，Griffin通过实验得出的人体站姿阻尼比(0.3 ～0.5)[3]接近;

(4)研究中发现的当人体与结构质量比发生变化时，等效阻尼比随之变化的现象在文献[10]中也有类似论述。

综上所述，根据理论分析结果、实验测试拟合曲线及与前人理论的对比验证情况，结论如下:

(1)由振型叠加法知，一般情况下不存在与人体精确多自由度模型动力学上完全等价的单自由度模型，但可通过调整其参数的办法获得与精确模型或实验结果的最佳数值逼近;

(2)人体的局部姿态可影响其单自由度等效模型的参数取值，例如本文研究中踮起脚尖站立导致等效自振频率增加，而举手动作使得等效阻尼比发生变化;

(3)由前述可推知根据结构动力学参数确定人体等效单自由度模型参数显然有利于获得更为准确的动力学分析结果。

[1]Subashi G H M J，Matsumoto Y，Griffin M J.Modelling resonances of the standing body exposed to vertical wholebody vibration:Effects of posture[J].Journal of Sound and Vibration，2008，317:400 －418.

[2]Matsumoto Y， Griffin M J. Modelling the dynamic mechanisms associated with the principal resonance of the seated human body[J].Clinical Biomechanics，2001，16:31－44.

[3]Matsumoto Y，Griffin M J.Mathematical models for the apparent masses of standing subjects exposed to vertical whole-body vibration [J].Journal of Sound and Vibration，2003，260:431 －451.

[4]Wei L，Griffin M J.Mathematical models for the apparent mass of the seated human body exposed to vertical vibration[J].Journal of Sound and Vibration，1998，212(5):855－874.

[5]Griffin M J.Handbook of human vibration[M].London:Academic Press Limited，1990.

[6]何浩祥，闫维明，张爱林.人行激励下梁板结构与人体耦合作用研究[J].振动与冲击，2008，27(10):130－133.HE Hao-xiang，YAN Wei-ming，ZHANG Ai-lin.Dynamic interaction between human and beam-slab structures under human walking excitation[J].Journal of Vibration and Shock，2008，27(10):130 －133.

[7]Dougill J W，Wright J R，Parkhouse J G，et al.Human structure interaction during rhythmic bobbing[J].The Structural Engineer，21 November，2006:32 －39.

[8]陈建英，方之楚.人－结构相互作用动力学建模研究[J].振动与冲击，2007，26(6):10－13.CHEN Jian-ying，FANG Zhi-chu.Study on modeling of human occupants-structure dynamic interaction[J].Journal of Vibration and Shock.2007，26(6):10－13.

[9]樊健生，李 泉，李全旺，等.考虑人－结构相互作用的楼盖振动控制研究[J].振动与冲击，2010，29(11):230－236.FAN Jian-sheng，LI Quan，LI Quan-wang，et al.Floor vibration control considering human-structure interaction[J].Journal of Vibration and Shock，2010，29(11):230 －236.

[10]Ebrahimpour A，Sack R L.Design live loads for coherent crowd harmonic movements[J].JournalofStructural Engineering，1992，118(4):1121 －1136.