一类多频线谱激励下的主动隔振控制方法

陈绍青，王 永，魏璀璨，姚太克

(中国科学技术大学 自动化系，合肥 230027)

近年来振动控制问题得到了人们的广泛关注。其中，隔振技术是振动控制的一个重要的研究方向[1]。按是否需要能源，隔振又可分为主动隔振与被动隔振。由于主动隔振能够克服被动隔振难以有效抑制低频振动的缺点，因此近年来日益受到重视[2－3]。

工程实践中存在着众多多频线谱激励下的振动控制问题。其中，包含振动频谱为一系列谐波分量以及多个独立的简谐波分量的情况[4]。对于此类振动问题，仅对基频或某频率分量振动进行控制并不能有效降低结构振动的水平，因此需要对多个线谱同时进行控制。

国内外对多线谱振动抑制问题已经开展了一些研究。在被动隔振方面，动力吸振器在许多结构振动控制问题中取得了良好的效果，但其有效吸振频带往往较小[5]，可以采用多自由度动力吸振器方法[6]或者多个单自由度动力吸振器进行一对一频率调谐的方法[5]消除结构的多频振动，但这类方法的缺点是要求的附加质量往往较大，且不便于调节。在主动隔振方面，赵冉等[7]针对电磁悬浮主动隔振系统，设计了自适应滑模单频隔振算法，通过仿真实验验证了算法的有效性;段小帅等[8]基于自行研制的磁悬浮隔振器，提出了采用自寻优前馈控制及时域滤波x-LMS(Filtered-X Least Mean Square)算法[9]的方案，较好地解决了隔振器的单频振动控制问题;张国庆等[10]针对多频线谱振动提出一种多通道解耦LMS自适应滤波方法，较好地解决了成倍频关系的多频谐波振动的控制问题。此外，基于频域的自适应滤波方法对于多频振动的控制较为有效，但是算法实现较为复杂[4]。

本文提出一种多频线谱激励下的自收敛LMS控制方法，通过多个窄带带通滤波器对多频激励信号及误差信号进行解耦，采用多个并行的自收敛变步长归一化LMS自适应滤波器，得到合成的多频振动控制量，控制一个单自由度的作动器，对多频振动进行隔离。将本文的方法应用于某型磁悬浮隔振器的隔振实验中，成功实现了对非倍频关系线谱激励下多频振动的有效抑制。

1 自适应前馈控制算法

基于有限脉冲响应(Finite Impulse Response，FIR)控制器的自适应前馈控制是振动工程领域中使用较为广泛的一种振动主动控制方法。其中，滤波x－LMS算法是目前为止应用最广泛的窄带振动消除方法。但这类算法由于需要辨识次级通道模型可能存在以下的问题:① 增加算法实现的复杂度;② 次级通道辨识若存在较大误差，将影响控制器的性能;③ 当次级通道为时变时，需要在系统中加入辅助输入以完成通道的在线辨识，这将影响最终的收敛结果[11－12]。

Zhou等[13]对滤波x－LMS算法进行了几何分析，指出当次级通道模型与真实模型相位误差不大于±90°，且步长因子满足一定条件时，算法始终是收敛的。进而Zhou等[11－12]将滤波 x－LMS算法的几何分析结果推广到了无需次级通道模型的情况，提出了一种能够自动判别权值更新方向的LMS控制算法，但该算法往往收敛较慢，不利于实际应用。

1.1 自收敛变步长归一化LMS算法

LMS算法的原理如图1所示。P(z)、S(z)分别代表初级通道和次级通道，W(z)是自适应滤波器，x(n)是参考信号，v(n)是目标点处附加的零均值噪声，它与x(n)无关，e(n)为误差信号。定义参考信号向量x(n)=[x(n)x(n－1) … x(n－M)]T，其中M是自适应滤波器的阶次。自适应滤波器系数的更新公式为:

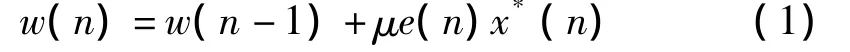
其中:μ是一个小的正实数。

对于一个单频输入Xω(n):

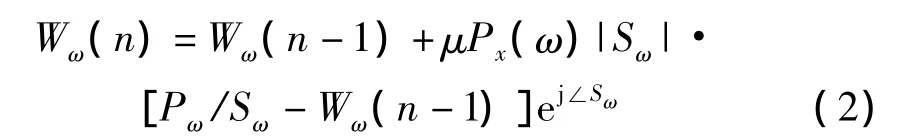
其中:∠Sω代表Sω的角度代表Sω的幅值。根据文献[11]的讨论结果，可以得到当步长满足。

图1 LMS算法原理图Fig.1 Block diagram of LMS algorithm

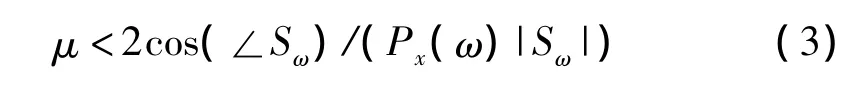
且∠Sω在±90°的范围内时，Wω(n)的更新公式依然适用，不需要次级通道模型最终也能收敛到最优值。如果∠Sω在±90°的范围外，自适应滤波器就会发散。此时，只需改变更新式(1)μ前的符号，Wω(n)的更新公式仍然收敛，即:

当然也可能有角度差刚好等于±90°的情况，此时只需对参考信号进行延迟输入处理即可。

文献[14]中作者对Zhou的算法进行了改进，建立起步长因子μ与误差e之间的指数函数关系，实现变步长算法;同时考虑到归一化能够改善LMS算法的鲁棒性，使系统具有更好的稳定性，提出了变步长归一化的步长因子:

其中:l为归一化数据的长度，α，β可根据实际情况选取。

无需次级通道模型的自收敛LMS控制算法流程如下[14]:

(1)初始化自适应滤波器的系数向量为零矢量，初始化用于评价信号能量的采集数据个数N、定步长μ、浮动因子δ，归一化数据长度 l，变步长因子系数α，β。

(2)先不更新自适应滤波器的系数，计算:

(3)采用定步长μ按式(1)更新自适应滤波器，测量误差信号能量 ξ2，如果|e(i)|＞(1+δ)emax则停止更新，并改变μ的符号。

(4)根据式(1)更新自适应滤波器，进而生成作动器的控制量。

(5)根据传感器采集的信号，按式(5)更新变步长因子μ(n)，并令式(1)中的μ=μ(n)，然后返回第(4)步，继续循环。

1.2 多频振动控制应用分析

上述LMS控制算法是在单频输入信号条件下展开分析的，利用信号的正交性可将相关结论推广到窄带甚至宽带输入信号的情况。考虑频域下的LMS算法权值更新式，在频域的每个子带中(子带大小与FFT的频率分辨率有关):

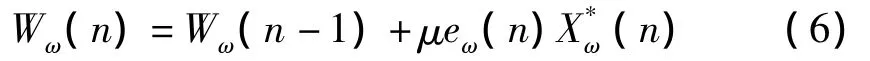
其中:

将式(7)代入式(6)得:

对式(8)两边取期望，并假设信号Xω(n)是平稳的且与滤波器权值不相关，各通道定常，则:

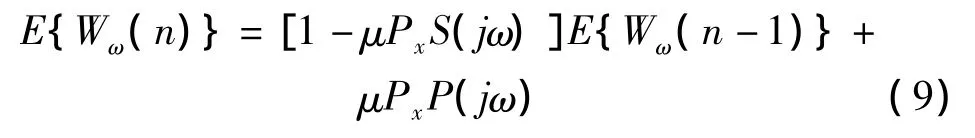
其中:Px=E{|Xω(n)|2}。将式x展开得:

随着迭代次数n的增大，式(10)满足如下条件时收敛:

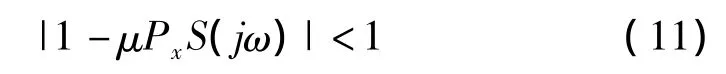
即:

展开可得:

式(13)与(3)的条件是等价的。在频域下只要所有频率点均满足式(13)即可，则对于多频或者宽频输入信号，收敛步长应满足:

注意到当式(14)中Re{S(jω)}＜0，则对应次级通道相位在±90°的范围外的情况(变为2，3象限上)，显然若在所有输入频率内Re{S(jω)}符号不统一，这种单收敛步长的算法将变得不稳定。故算法在输入信号频率通带的次级通道相位响应应满足:

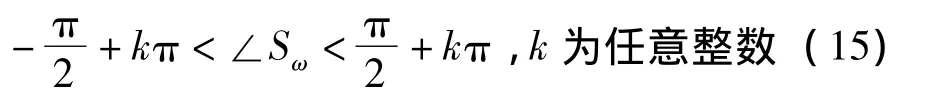
的条件。

当输入的多频或宽频信号中部分频率的次级通道相位响应不满足式(15)时，算法执行过程中不论如何变更步长因子的符号也无法得到收敛解;而当满足式(15)的相位条件时，假如输入信号各频率成分能量相差很大，满足收敛条件(14)的μ值过小，将导致收敛速度过慢。总之，由于算法中只有一个变步长因子，其选取难以兼顾多个频率振动控制的需求，应用范围是有限的。

1.3 时域多通道解耦的自适应滤波算法结构

针对上述自收敛LMS控制算法在处理多频及宽频振动控制问题上的限制和不足，提出一种时域多通道解耦的自适应滤波算法结构。即采用多个并行的自收敛变步长归一化LMS自适应滤波器，采用带通滤波器对多频参考信号及误差信号进行解耦，使得每个通带内输入信号的次级通道相位响应满足式(15)的条件。多通道解耦算法的结构如图2所示。

简单起见，假设待控制对象的振动频谱由N条离散的线谱组成，假定N=3，对应的频率分别为f1、f2、f3。图中X为与减振目标点振动相关的参考信号，也包含频率成分f1、f2、f3;d(t)为施加到减振对象的外部扰动;W1(z)、W2(z)、W3(z)为三个并行的自收敛变步长归一化LMS自适应滤波器;假定f1、f2、f3频率间隔足够大，可以设计带通滤波器filter1、filter2、filter3，通带分别为[fL1fH1]、[fL2fH2]、[fL3fH3]，并满足:

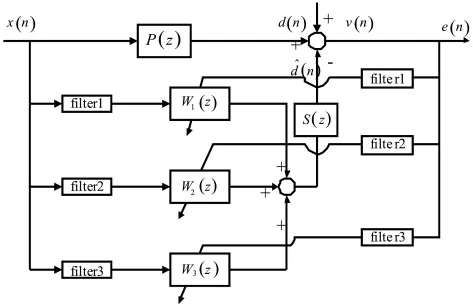
图2 多通道解耦算法结构图Fig.2 Block diagram of multi-channel decoupling algorithm

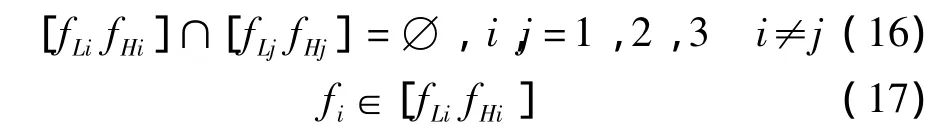
通过各个带通滤波器提取谱线对应频率成分的时域信号，采用自收敛变步长归一化LMS算法独立地调整各个控制滤波器系数，最终合成多频线谱振动的控制信号。由式(16)、式(17)知，各个自适应滤波器之间是相互独立的，可以针对不同频率成分的能量大小选取不同的步长因子，从而对各频率成分都起到有效的抑制作用。

此外，即使是对于宽频甚至更复杂频谱的振动控制问题，只要多通道解耦的各个滤波器的参数选择合适，运用该方法应能比单收敛步长控制方法收敛速度更快，得到更好的振动隔离效果。

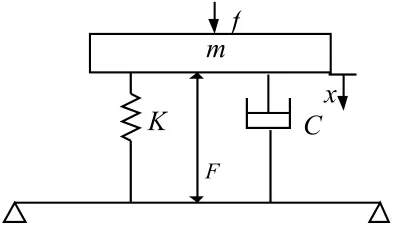
图3 磁悬浮隔振器机理模型Fig.3 The model of a magnetic suspension isolator

1.4 磁悬浮隔振器电磁力模型

本文涉及的磁悬浮隔振器为主被动复合式隔振器，该隔振器在被动隔振单元的基础上并联一个主动电磁作动单元，以对设备和结构施加作用力，其机理模型如图3，其中K为弹簧刚度，m为隔振器负载重量，f为激振力，x为负载位移，F为电磁力，C为弹簧阻尼。通过基于MTS809的实验建模方法[15]，可得隔振器上下电磁铁的电磁力公式:

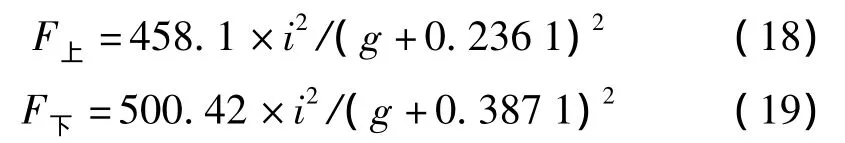
其中:F上，F下分别代表上、下电磁铁产生的磁力，i为输入到电磁铁功率放大器的驱动电流，g为磁隙大小。

为了在磁悬浮隔振系统中应用自收敛变步长归一化LMS算法，需要加入电磁力反解过程[14]。在控制过程中，需要根据气隙值的大小在两个电磁力公式之间切换。假定系统未受扰动时位移传感器的输出是零，如果采样时刻位移传感器的输出为负值，表明弹簧继续压缩，隔振器下方的基础受到向下的压力。此时需要下电磁铁工作，使衔铁吸引下电磁铁以对基础产生向上的作用力，此时在控制算法中选择下电磁铁的模型进行计算。上电磁铁与位移传感器输出正值的关系类似。

2 实验系统及方案

磁悬浮隔振器的隔振实验平台如图4所示。

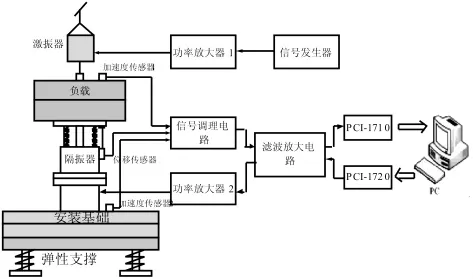
图4 磁悬浮隔振实验平台系统示意图Fig.4 Block diagram of the experimental platform

整个实验系统由两大部分构成:一部分是系统的机械部分，包括安装基础、负载、激振器和磁悬浮隔振器，它们分别担当了控制对象，扰动源和执行机构的角色;另一部分是系统的电控部分，包括加速度传感器、信号采集与调理模块、控制器、功率放大器等。

其中，负载为重量约为500 kg的质量块，安装基础为由3个配重质量构成的约1 000 kg的质量块，安装基础底部的弹性支撑为5个上海环星减振器厂的ZTE2－320型弹簧阻尼隔振器，其与安装基础构成的系统的固有频率约为2.8 Hz。

设计实验步骤如下:

(1)实验系统安装:按照图4所示连接隔振系统各个部件。PC机通过PCI1710板卡采集四路信号:基础加速度信号用于生成误差信号，相对位移信号用于计算电磁作动器的气隙大小，负载加速度信号用于监测负载加速度的变化，阻抗头用于监测激振力信号。激振模块信号发生器的输出信号用作参考信号;通过PCI1720板卡输出两路信号，它们经过功率放大器后驱动上下两块电磁铁。

(2)3频激励下的主动隔振实验测试:采用PC机生成6 Hz、13 Hz和32 Hz的不成倍频关系的3频数字激振信号，经D/A转换成模拟信号，驱动激振器激励实验系统。滤波器的通带分别为[4 Hz，8 Hz]、[10 Hz，16 Hz]、[28 Hz，36 Hz]。系统采样频率设为 1 000 Hz，实验时间为120 s，实验过程中前、后20 s不施加振动主动控制，前20 s为起振过程，中间80 s施加振动主动控制。

3 实验结果分析

图5所示为实验过程中与激振器联接的阻抗头采集到的激振力时域信号(31 s到32 s)，图6所示为激振力的频谱图，可见激振力中除6 Hz、13 Hz、32 Hz的不同能量的频率成分分量外，还包含由于机械系统非线性引起一些小谐波分量。

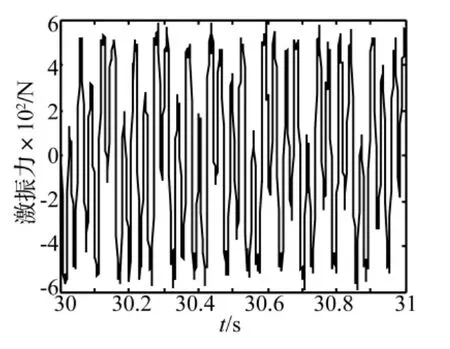
图5 3频激振时激振力时域曲线Fig.5 Time sequences of exciting force

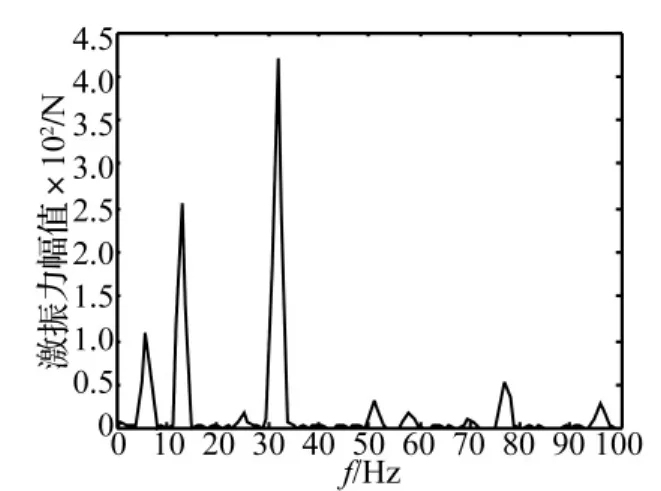
图6 3频激振时激振力频谱Fig.6 Frequency spectra of exciting force

图7 3频激振时基础加速度响应Fig.7 Acceleration response of target point

图8 主动隔振前后基础加速度频谱Fig.8 Frequency spectra of acceleration response before＆after control

实验效果如图7所示，采用减振目标点的加速度响应来评价主动隔振效果，其计算公式为L=10log，式中a1为控制后目标点的加速度响应幅值，a2为控制前目标点的加速度响应幅值，a2为振动加速度的信号能量，计算得主动隔振效果约为14.52 dB。由图8和表1易见，采用多通道解耦的自收敛变步长归一化LMS算法，在单个磁悬浮隔振器的控制作用下，6 Hz、13 Hz、32 Hz的振动得到了显著的抑制，分别下降了15.5 dB、16.54 dB、7.05 dB，由于机械系统非线性引起的其他谐波分量振动也得到抑制，基础的振动水平大大降低，充分验证了控制器和隔振器的有效性。

表1 主动隔振在各主要频率成分处的减振效果Tab.1 Effect of active control on main frequencies

4 结论

本文主要研究了多频线谱激励下的振动控制问题，通过引入带通滤波器进行多通道解耦，将自收敛变步长归一化LMS算法拓展到了多频振动控制的情况，利用多个并行的自适应滤波器实现了各线谱振动的有效抑制。上述算法在某型磁悬浮隔振器上得到了成功应用，充分验证了该方法的有效性。

[1]江国和，沈荣瀛，华宏星，等.舰船机械设备冲击隔离技术研究进展[J].船舶力学，2006，10(1):135－144.

[2]张 磊，付永领，刘永光，等.主动隔振技术及其应用与发展[J].机床与液压，2005，2:5－8.

[3]玉 辉，靳晓雄，肖 勇.振动主动控制技术的研究与发展趋势[J].上海汽车，2006，7:29－31.

[4]Jiang K J，Zhu C S.Multi-frequency periodic vibration suppressing in active magnetic bearing-rotor systems via response matching in frequency domain[J].Mechanical Systems and Signal Processing，2011，25(4):1417 －1429.

[5]Sun H L，Zhang P Q，Chen H B，et al.Application of dynamic vibration absorbers in structural vibration control under multi-frequency harmonic excitations[J].Applied Acoustics，2008，69(12):1361 －1367.

[6]李 俊，金咸定，刘见华.多自由度无阻尼动力吸振器的理论研究[J].振动、测试与诊断，2003，23(2):99－102.

[7]赵 冉，王 永.基于自适应滑模控制的主动磁悬浮隔振系统[J].自动化与仪表，2008，23(10):4－8.

[8]段小帅，梁 青，王 永.磁悬浮隔振器的自寻优前馈控制[J].船舶力学，2010，14(7):795－799.

[9]梁 青，段小帅，陈绍青，等.基于滤波x-LMS算法的磁悬浮隔振器控制研究[J].振动与冲击，2010，29(7):201－203.

[10]张国庆，王 永，陈 光.一类多频线谱振动的主动控制方法[J].南京理工大学学报(自然科学版)，2005，29(z1):37－40.

[11]Zhou D Y.ANC algorithms that do not require identifying the secondary path[C].//IEEE International Conference on Acoustics，Speech，and Signal Processing，2005，3:125－128.

[12]Zhou D Y，DeBrunner V.A new active noise control algorithm that requires no secondary path identification based on the SPR property[J].//IEEE Transactions on Signal Processing，2007，55(2):1719－1729.

[13]Zhou D Y，DeBrunner V E，DeBrunner L，et al.Geometric analysis of filtered-X LMS algorithms[C].//IEEE/SP 13th Workshop on Statistical Signal Processing，2005:127－132.

[14]陈绍青，王 永.基于磁悬浮隔振器的主动隔振控制实验研究[J].东南大学学报(自然科学版)，2010，S1:61－66.

[15]孟令雷，倪向贵，王 永，等.基于MTS809的磁悬浮隔振器电磁力测量[J].自动化与仪表，2009，24(3):4－7.