斜拉桥与引桥地震碰撞影响因素研究

张文学，王景景，鲍 艳

(北京工业大学 建筑工程学院，北京 100124)

随着经济的发展，人们对交通线的依赖性越来越强，一旦地震使交通线遭到破坏，可能导致的生命财产损失以及间接经济损失非常巨大。几次大地震一再显示了桥梁工程破坏的严重后果，也一再表明桥梁抗震研究的重要性[1－3]。虽然专家学者对斜拉桥的抗震问题进行了大量的研究，但目前关于斜拉桥抗震研究多以斜拉桥为研究对象，关于斜拉桥与引桥之间碰撞问题的研究较少。由斜拉桥与其引桥动力特性相差较大，在纵向地震作用下有导致发生非同向振动的可能，造成主桥与其引桥伸缩缝处相邻梁体的碰撞和较大的梁体相对位移，导致伸缩缝破坏和落梁[4－7]。如日本阪神地震中西宫港大桥与主桥相邻引桥发生落梁，汶川地震引起了紫坪铺水库大桥引桥落梁。过去对这一现象研究不够深入，而现行的抗震设计规范对此没也有明确规定，因此有必要对主桥与引桥之间的碰撞效应进行系统研究，分析相关参数对斜拉桥主桥与引桥之间碰撞效应的影响，以便为斜拉桥的抗震设计提供参考。

1 工程背景及分析模型

以某九江大桥为分析对象，桥梁分析模型跨径组合为5×50 m等截面预应力砼连续箱梁+(70+75+84+818+233.5+124.5)m双塔钢箱梁斜拉桥+5×50 m等截面预应力砼连续箱梁，伸缩缝采用D1600型。采用sap2000软件，利用空间梁单元模拟主梁、主塔和墩柱，其中主梁采用单梁式力学模型，斜拉索采用空间桁架单元，考虑拉索垂度效应和恒载作用对结构刚度的影响，采Ernst公式修正拉索弹性模量。引桥中离主桥较近的中墩为固定墩，其余为纵桥向滑动、横桥向固定，有限元计算模型如图1所示。

分析时结构的阻尼比取为5%，为模拟主桥与引桥之间的碰撞效应，在伸缩缝处采用如图2所示的接触单元。接触单元的非线性力－位移关系为:

式中:d0为伸缩缝初始间隙，根据工程具体情况计算中取伸缩缝的初始间隙为80 cm;xs为伸缩缝处相邻梁体的相对位移;k为接触刚度，根据相关文献的研究成果，并考虑到本分析模型中引桥长度达250 m，因此分析 k 取0.5 倍引桥箱梁轴向刚度[8－10]。

碰撞过程中的能量损失采用阻尼器模拟，其阻尼的大小与碰撞过程的恢复系数e有关，本分析中取e=0.65，根据恢复系数e和公式(2)计算阻尼器参数，式中m1和m2分别为伸缩缝相邻梁体的质量。

图1 结构模型Fig.1 Structure mode

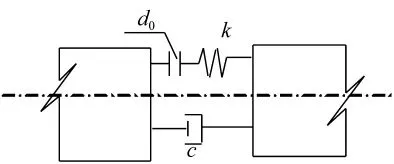
图2 伸缩缝模型Fig.2 Expansion joint mode

为使分析更具代表性，对不同场地类型分别选取了如表1所示的各典型地震波作为地震输入，调幅后的加速度峰值为0.60 g。

2 斜拉桥碰撞影响因素分析

以表1所列不同场地地震波作为纵向地震动输入，详细分析了场地类型、斜拉桥重心高度和引桥结构形式因素对斜拉桥主桥与引桥之间碰撞影响情况分析如下。以下分析数据均为每类场地3条波的平均值。

2.1 场地类型的影响

为使分析更具有代表性，通过改变下塔柱高度h1，而保持上塔柱高度h2=h－h1不变的方式，分别取斜拉桥下塔柱与总塔高之比(以下简称重心高度)h1/h为1/15、3/15、5/15进行建模，分析场地类型对斜拉桥与引桥之间碰撞的影响，分析结果如图3所示，由此可知:

(1)场地类型对斜拉桥与引桥之间的碰撞响应有较大的影响。在Ⅱ、Ⅲ类场地条件下，考虑碰撞后引桥固定墩墩底弯矩比没考虑碰撞时有较大幅度的增加，最大增加幅度达90%以上。而在Ⅰ、Ⅳ类场地条件下考虑碰撞后引桥固定墩墩底弯矩比没考虑碰撞时有所降低，降低幅度不到30%。

(2)在Ⅰ、Ⅱ和Ⅳ场地条件下，碰撞对斜拉桥主塔塔底弯矩响应有所影响，但影响幅度较小，在±10%左右。而在Ⅲ类场地条件下，考虑碰撞后主塔塔底弯矩响应比没考虑碰撞有所降低，降低幅度在30%以内。

(3)考虑碰撞后斜拉桥与引桥伸缩缝处的相对位移明显降低，且降低幅度受场地类型影响较大，Ⅰ类场地条件下降低幅度为10% ～20%，而在Ⅳ类场地条件下最大降低幅度达70%以上。

(4)场地类型对斜拉桥与引桥之间的碰撞力有较大影响，在Ⅰ、Ⅳ场地条件下碰撞力相对较小，而在Ⅱ、Ⅲ类场地条件下碰撞力明显增加。Ⅱ、Ⅲ类场地条件下碰撞力约为Ⅰ、Ⅳ场地条件下碰撞力的6倍左右。

表1 典型地震波Tab.1 Typical earthquake wave

图3 场地类型对碰撞的影响Fig.3 Impacting influence of site-type

图4 斜拉桥重心高度对碰撞响应的影响Fig.4 Impacting influence of gravity center high

图5 引桥结构形式对碰撞的影响Fig.5 Impacting influence of approach-bridge structure form

2.2 重心高度的影响

为分析斜拉桥重心高度对其与引桥之间碰撞的影响情况，分别取斜拉桥下塔柱高度与总塔高之比h1/h为1/15～5/15，对不同场地类型条件下斜拉桥与引桥之间的碰撞响应进行了详细的分析，分析结果如图4所示。由此可知:

(1)重心高度对斜拉桥与引桥之间的碰撞响应有一定影响。在相同场地类型条件下，随着h1/h的不同，考虑碰撞时引桥固定墩墩底弯矩与没考虑碰撞时引桥固定墩墩底弯矩之比的变化幅度高达40%;考虑碰撞时斜拉桥塔底弯矩与没考虑碰撞时塔底弯矩之比的变化幅度高达30%。

(2)在不同的场地类型条件下，考虑碰撞与没考虑碰撞引桥固定墩墩底弯矩之比及斜拉桥塔底弯矩之比受h1/h的影响程度存在较大差异。

(3)在相同场地类型条件下，随着h1/h的不同，考虑碰撞与没考虑碰撞伸缩缝相对位移之比的变化幅度高达35%;且随着场地类型的不同，其变化幅度也有所不同。

(4)在相同场地类型条件下，随着h1/h的不同，考虑碰撞与没考虑碰撞伸缩缝处碰撞力之比的最大变化幅度高达50%以上;且随着场地类型的不同，其变化幅度存在较大差异。

2.3 引桥结构形式影响

为分析引桥结构形式对斜拉桥与引桥之间碰撞的影响，分别对连续梁结构和简支梁结构引桥进行了对比分析，远离主桥的桥墩为简支梁引桥固定墩，分析结果如图5所示，由此可知:

(1)不论是简支梁结构引桥，还是连续梁结构引桥，碰撞对引桥固定墩的墩底弯矩响应均有较大的影响。与连续梁引桥结构相比，简支梁引桥固定墩墩底弯矩受碰撞的影响更显著，特别是在Ⅱ类场地条件下，考虑碰撞后简支梁引桥固定墩墩底弯矩约为不考虑碰撞效应时的4倍，在Ⅲ类场地条件下，考虑碰撞后简支梁引桥固定墩墩底弯矩约为不考虑碰撞效应时的2倍，而Ⅰ、Ⅳ在场地条件下考虑碰撞后引桥的固定墩墩底弯矩响应却比不考虑碰撞时有所降低，但降低幅度不大。

(2)碰撞对不同结构引桥梁端纵向位移响应的影响与引桥固定墩墩底弯矩响应的影响规律基本相同。

(3)不论是简支梁结构引桥，还是连续梁结构引桥，碰撞斜拉桥主塔塔底的弯矩响应均有所影响，但其影响程度远不如对引桥固定墩墩底弯矩影响明显，影响幅度均在±10%以内。

(4)不同引桥结构形式对主桥与引桥之间碰撞力的影响较小，而场地类型对主桥与引桥之间碰撞力的影响非常明显，Ⅱ、Ⅲ场地条件下的碰撞力明显高于Ⅰ、Ⅳ场地条件下的碰撞力。

3 结论

以某九江斜拉桥为工程背景，建立了包括引桥在内的考虑碰撞效应的分析模型，对斜拉桥与引桥之间的碰撞问题进行了较为系统的研究，得出如下主要结论:

(1)碰撞不仅对引桥的地震响应有较大影响，而且对斜拉桥主桥地震响应也有一定影响。

(2)在本文所分析的各种影响因素中，场地类型对引桥与主桥之间碰撞的影响最为明显，相同结构不同场地类型情况下，主桥与引桥之间的碰撞效应相差很大。因此，在进行斜拉桥抗震设计时应根据具体的场地类型进行具体分析。

(3)斜拉桥的重心高度对主桥与引桥之间的碰撞响应有一定影响，但其影响不具有规律性。

(4)通过对比不同引桥结构形式对碰撞效应的影响可知，从碰撞响应角度考虑斜拉桥的引桥不宜采用简支梁结构。

[1]范立础.桥梁抗震[M].上海:同济大学出版社，1997.

[2]王军文.非规则梁桥在地震作用下的碰撞效应及防落梁措施研究[D].上海:同济大学，2005.

[3]王东升，冯启民，凌贤长，等.桥梁非线性地震反应分析若干问题研究现状[J].地震工程与工程振动，2002，22(1):61－66.

[4]Nazmy A S，Abdel-Ghaffar A M.Non-linear earthquakeresponse analysis of long span cable-stayed bridge:theory[J]. Earthquake Engineering and Structural Dynamics，1990，19:45 －62.

[5]Chau K T，Wei X X，Guo X，et al.Experimental and theoretical simulations of seismic poundings between two adjacent structures[J].Earthquake Engng.Struct.Dyn.，2003，32:537 －554.

[6]Chau K T，Wei X X.Pounding of structures modelled as nonlinear impactsof two oscillators[J].Earthquake Engng.Struct.Dyn.，2001，30:633 －651.

[7]王东升，杨海红，王国新.考虑邻梁碰撞的多跨长简支梁桥落梁震害分析[J].中国公路学报，2005，18(3):54－59.

[8]李建中，范立础.非规则梁桥纵向地震反应及碰撞效应[J].土木工程学报，2005，38(1):84 －90.

[9]东 升，冯启民，王国新.基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型[J].工程力学，2004，21(2):157－166.

[10]王东升，王国新，冯启民.桥梁结构地震反应邻梁碰撞分析等效刚体模型[J].工程力学，2004，21(4):81－85.