噪声扰动下RLC串联谐振电路随机共振的数值研究

涂水林，邬正义，吴正阳

(常熟理工学院 物理与电子工程学院，常熟 215500)

自从Benzi等在研究古气象冰川问题时提出随机共振概念以来，随机共振的理论和实验研究引起了人们的极大兴趣。传统的随机共振是指在含有噪声的非线性系统中合适的噪声强度可以使得弱信号驱动下的输出信噪比达到某一最大值，其本质是部分噪声能量转化为了信号能量。随着研究的不断深入，随机共振的研究范围愈来愈得到拓展，从起初的非线性系统[1－2]到乘性色噪声或分段噪声驱动下的线性系统[3－10]，从传统的随机共振到广义的随机共振[11－15]等。

广义随机共振是指在有噪声的系统中，由于输入信号和噪声的协作效应，系统输出幅值或信噪比增益是噪声或输入信号的某个参数(噪声强度、激励信号的幅度或频率等)的非单调函数这样一种非线性现象。信噪比增益定义为输出信噪比与输入信噪比的比值，其与信噪比一直是传统随机共振的主要测度指标，若其取值大于1，表明系统对输入有用信号可能有增强和改善作用，但也可能是系统对背景噪声相对于有用信号而言进行了更强的抑制。进一步确认需引入另一测度指标——谱功率放大系数。

谐振是交流电路中一种特定的工作状态，被广泛地应用于实际电路中。谐振电路通常是由电阻、电感、电容元件构成。本文采用四阶Runge-Kutta算法，以信噪比增益和谱功率放大率为随机共振测度指标，研究电容参数和激励信号均受高斯白噪声扰动时欠阻尼、临界阻尼和过阻尼三种情况下的RLC串联谐振电路的随机共振现象。研究过程表明，仅仅依据信噪比增益大于1并不能说明噪声能量转化为了信号能量或信号能量得到了加强和改善，只有在同时满足谱功率放大率大于1的条件下，才能得出上述结论。研究结论使得将欠阻尼RLC串联谐振电路应用于微弱信号检测成为可能。

图1 RLC串联谐振电路Fig.1 RLC series resonant circuit

1 RLC谐振电路模型

描述图1所示RLC串联谐振电路的动态方程如式(1)所示。

式中:ui(t)为系统激励信号;uo(t)为系统输出信号。将式(1)进行拉普拉斯变换，并令，则系统的传递函数为:

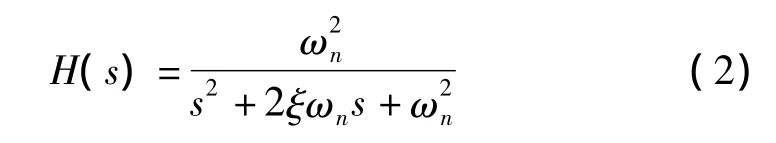
ξ和ωn分别是式(1)系统无噪声时的阻尼系数和固有频率。从传递函数的形式可以看出，这是一个典型的二阶线性系统。当0＜ξ＜1、ξ＞1、ξ=1时，即系统参数时，系统将分别工作于欠阻尼、过阻尼、临界阻尼三种工作状态。

考虑系统激励信号为强高斯白噪声ζ1(t)背景下的弱正弦信号和电容参数C受到高斯白噪声ζ2(t)的扰动，即 ui'(t)=Asin(2πf0t)+ ζ1(t)，C'=C(1+ζ2(t))，式中A是输入信号的幅度，f0是输入信号的频率，C为无扰动时的电容值，ζ1(t)、ζ2(t)为高斯白噪声，其均值和相关函数为:

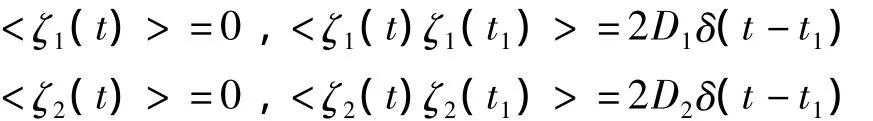
式中:D1(量纲为[伏特]2)、D2(无量纲)分别是噪声ζ1(t)、ζ2(t)的强度。这时，式(1)变为:

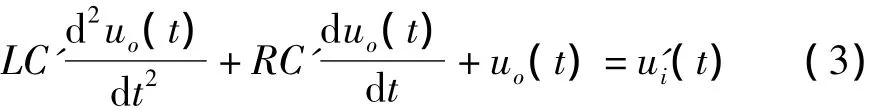
2 数值分析方法

式(3)描述的是一个二阶微分方程的初值问题，可以归结为一阶微分方程组来求解。引进新变量x=du0/dt，则式(3)可以化为一阶方程组初值问题:

为了使得数值计算具有较好的精度，采用了四阶龙格－库塔算法，具体形式为:

式中:

式中:uin，uon分别表示系统激励信号 ui'(t)=Asin(2πf0t)+ζ1(t)、输出信号uo(t)的第n个采样值，C'(n)为电容受噪声扰动后第n时刻的值，h=1/fs为时间步长，等于采样频率fs的倒数。

3 随机共振测度指标

随机共振的定量描述需要测度指标来刻画，随着随机共振研究的不断深入，随机共振测度测度指标也一直是随机共振研究的一个重要方面。常用的随机共振测度指标有信噪比增益、信噪比、谱功率放大率、线性响应敏感度以及常用在非周期随机共振上的互相关系数等。在传统的随机共振研究中，衡量随机共振现象是否发生的依据是系统输出信噪比对输入噪声强度呈现出非单调函数关系，而现在除了这一标准以外，根据广义随机共振的概念，若系统输出幅值或信噪比增益是噪声或输入信号的某个参数(噪声强度、激励信号的幅度或频率等)的非单调函数也可以就此判断系统发生了随机共振现象。从系统对信号增强和改善的角度看，最直观的衡量指标是信噪比增益和谱功率放大率，若这两项指标均大于1才能说明系统具有增强和改善有用信号的作用。

在信号检测及通信等领域中，常用的信噪比定义为:

式中:S(f0)为信号功率，是信号功率谱中f0频率处的幅值，P为信号总功率，包括信号功率和噪声功率，减去S(f0)后剩下的即为噪声功率。

假设系统激励信号为强高斯白噪声背景下弱正弦信号Acos(2πf0t)+ζ1(t)，经过采样频率为fs的采样后得到长度为N的离散序列x(n)，通过四阶Runge-Kutta算法数值求解得到系统的输出信号y(n)，对y(n)进行FFT处理，可得其频谱分布Y(k):

设Y(k0)为输出端信号频谱中f0频率分量的幅值，且有，根据信噪比定义可得到输出端信噪比:

同理，输入端信号序列x(n)的信噪比可由下式得到:

式中:X(k0)为输入端信号频谱中f0频率分量的幅值。

而信噪比增益和谱功率放大率则定义为:

式中:SNRgain为信噪比增益，SNRout为输出端信噪比，SNRin为输入端信噪比。

4 数值结果及分析

根据RLC串联谐振电路动态方程表达式(3)，令L=25 mH，C=1 000 μF，则系统无扰动时谐振频率为31.831 0 Hz。改变R的取值使系统分别处于欠阻尼、临界阻尼和过阻尼状态，然后在考虑电容参数和弱输入激励信号受到高斯白噪声扰动情况下，采用四阶龙格－库塔算法，仿真和分析信噪比增益和谱功率放大率与激励信号频率和噪声强度的关系。选择采样频率fs=180f0，步长 h=1/fs，采样点数 N=1 024，信噪比增益和谱功率放大率均取100次计算的平均值。

4.1 欠阻尼状态

首先来看欠阻尼RLC串联电路谐振时对噪声能量的作用情况。

对式(3)描述的系统，令R=1 Ω，此时阻尼系数ξ=0.1，系统处于欠阻尼状态。再令 f0=31.831 0 Hz，A=0.1，D1=2，D2=0.01，因此时激励信号频率等于系统无噪声扰动时的谐振频率，故系统也可认为处于谐振状态。通过仿真得到系统输入、输出信号及其频谱图如图2所示。图2(a)为弱正弦有用信号，幅值为0.1，在与噪声强度为2的高斯白噪声叠加后时域波形如图2(b)所示，信号已经完全淹没于噪声中，对其进行FFT分析，得到噪声背景下信号频谱图2(c)，从图2(c)中无法确定有用信号的存在;将该含噪声信号作为激励信号输入式(3)系统，并对系统输出信号进行频谱分析，得到输出信号频谱图2(d)，可以看出，在图2(d)中很容易分辨出有用信号频率，表明系统在谐振状态下具有很好的信噪比增益和谱功率放大率。若令A=0，仅仅将噪声强度为2的高斯白噪声输入式(3)系统，其输出频谱图如图2(e)所示。

图2 欠阻尼RLC串联谐振电路谐振时输入、输出信号及其频谱图Fig.2 The input and output signals and their spectrums of underdamped RLC series resonant circuit at resonance

图2 很清楚地显示了RLC串联谐振电路的选频放大特性，它不仅能放大电路谐振频率处的有用信号，而且能选择性地增强谐振频率处的噪声信号。这就为将噪声能量转化为信号能量提供了条件。在图2(d)、(e)中还可看出系统对大于谐振频率的高频噪声信号具有很强的抑制作用。这和无扰动时欠阻尼二阶系统频率特性在低频段呈现低通，频率处出现谷峰，高频段以－40 dB/十倍频程下降的低通特性相符，表明欠阻尼二阶系统在系统参数受到噪声扰动后其频率特性并未发生根本变化。

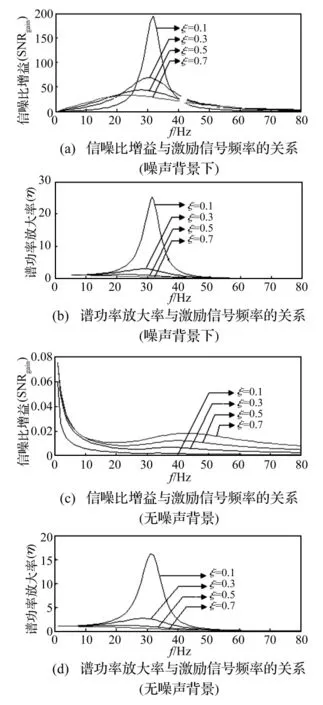
图3 欠阻尼情况下信噪比增益和谱功率放大率与激励信号频率的关系Fig.3 The relation curves of SNR gain and spectral power magnification of underdamped circuit with the excitation signal frequency

保持上述其它参数不变，仅改变激励信号频率f0，并按照式(8)～(11)计算信噪比增益 SNRgain和谱功率放大率η，得到欠阻尼情况下信噪比增益和谱功率放大率与激励信号频率的关系曲线如图3(a)、(b)所示;令D1=0，重复上述仿真计算得到无噪声背景下信噪比增益和谱功率放大率与激励信号频率的关系曲线如图3(c)、(d)所示。对比图 3(a)、(b)和(c)、(d)，可以很明显地看出输入信号含有噪声时系统输出的信噪比增益和谱功率放大率比无噪声背景时要大得多。且信噪比增益和谱功率放大率在外加激励信号频率接近系统固有频率时出现了最大值，表明信噪比增益和谱功率放大率是激励信号频率的非单调函数。RLC串联谐振电路是一个无源系统，在输入噪声强度不变的情况下信噪比增益和谱功率放大率出现峰值，且均大于1，这说明有用信号的能量得到了加强和改善，部分噪声能量转化为了信号能量，系统发生了随机共振现象。

由图3还可看出，信噪比增益和谱功率放大率的峰值高度均随着阻尼系数ξ的增大而减小，且共振峰随着ξ增大而向激励信号频率变小的方向移动，所以较小的阻尼系数有利于信噪比增益和谱功率放大率的提高。

图4 欠阻尼情况下信噪比增益和谱功率放大率与噪声强度的关系Fig.4 The relation curves of SNR gain and spectral power magnification of underdamped circuit with the noise intensity

图4 为欠阻尼状态下电路谐振时信噪比增益和谱功率放大率与噪声强度的关系曲线。为便于分析，令ζ1(t)=ζ2(t)，D1=D2=D(下同)。图 4(a)说明随着噪声强度D的增大，信噪比增益也有峰值出现，即信噪比增益对噪声强度呈现非单调依赖关系。图4(b)表明谱功率放大率对噪声强度为单调增关系，且其取值在ξ＜0.7时均大于1，这说明欠阻尼状态下电路谐振时信号能量确实得到了改善。

4.2 临界阻尼状态

保持L、C参数值不变，将电阻R调整为10 Ω，系统处于临界阻尼状态。图5为临界阻尼情况下信噪比增益与激励信号频率和噪声强度的关系曲线，图6为临界阻尼情况下谱功率放大率与激励信号频率和噪声强度的关系曲线。从图5可以看出，信噪比增益是激励信号频率和噪声强度的非单调函数，系统存在随机共振现象。但图6显示在信噪比增益取得峰值时，其对应谱功率放大率均小于1，这说明信噪比的改善并不一定意味着信号能量的提高。

图5 临界阻尼情况下信噪比增益与激励信号频率和噪声强度的关系Fig.5 The relation curves of the SNR gain of critical damping circuit with the excitation signal frequency and noise intensity

图6 临界阻尼情况下谱功率放大率与激励信号频率和噪声强度的关系Fig.6 The relation curves of the spectral power magnification of critical damping circuit with the excitation signal frequency and noise intensity

4.3 过阻尼状态

继续调整电阻R的取值，使其分别为11 Ω、15 Ω、20 Ω、25 Ω、30 Ω，电路此时处于过阻尼状态。图 7 和图8分别为过阻尼状态下信噪比增益和谱功率放大率与激励信号频率和噪声强度的关系曲线图。从图7可以看出，信噪比增益依然是激励信号频率和噪声强度的非单调函数，系统同样存在随机共振现象。图8与图6显示的结果一样，即在临界阻尼和过阻尼两种状态下，尽管信噪比增益在某一噪声强度下取得了最大值，且取值大于1，但此时对应谱功率放大率小于1，结合分析表达式(6)，说明此时系统输出信号中高频噪声能量相比信号能量得到了更大的抑制，而信号能量本身并未得到加强。

图7 过阻尼情况下信噪比增益与激励信号频率和噪声强度的关系Fig.7 The relation curves of the SNR gain of overdamping circuit with the excitation signal frequency and noise intensity

图8 过阻尼情况下谱功率放大率与激励信号频率和噪声强度的关系Fig.8 The relation curves of the spectral power magnification of overdamping circuit with the excitation signal frequency and noise intensity

5 结论

本文采用四阶Runge-Kutta算法，以信噪比增益和谱功率放大率为随机共振测度指标，通过数值仿真，研究了电容参数受高斯白噪声扰动时欠阻尼、临界阻尼和过阻尼三种情况下的RLC串联谐振电路的随机共振现象。仿真分析结果表明:

(1)参数扰动下RLC串联谐振电路在一定条件下的欠阻尼、临界阻尼和过阻尼状态均存在随机共振现象。

(2)临界阻尼和过阻尼情况下尽管信噪比增益在一定条件下也是噪声强度和输入信号频率的非单调函数，但此时谱功率放大率取值小于1，电路发生了随机共振现象，改善了信噪比，信号能量却并未得到加强。

(3)在欠阻尼情况下，谐振状态时的电路发生随机共振现象非常明显，尤其阻尼系数越小随机共振效果越好。这一结论说明欠阻尼RLC串联谐振电路可以利用随机共振机制达到强噪声背景下微弱信号检测的目的。

[1]McNamara B，Wiesenfeld K.Theory of stochastic resonance[J].Phys.Rev.A，1989，39(9):4854 －4869.

[2]Gammaitoni L，Habnggi P，Jung P，et al.Stochastic resonance[J].Rev.Mod.Phys，1998，70(1):223 －287.

[3]郭 锋，周玉荣，蒋世奇，等.具有乘性噪声的线性系统的随机共振[J].电路与系统学报，2008，13(2):6 －8.GUO Feng，ZHOU Yu-rong，JIANG Shi-qi，et al.Stochastic resonance in a linear system with multiplicative noise[J].Journal of Circuits and Systems，2008，13(2):6 －8.

[4]郭 锋，周玉荣，蒋世奇，等.具有乘性噪声的线性振荡器的随机共振[J].电子科技大学学报，2008，37(1):77－80.GUO Feng，ZHOU Yu-rong，JIANH Shi-qi，et al.Stochastic resonance with multiplicative noise in a linear oscillator[J].Journal o f Universit y of Electronic Science and Technology of China，2008，37(1):77 －80.

[5]宁丽娟，徐 伟.信号调制下分段噪声驱动的线性系统的随机共振[J].物理学报，2009，58(5)，2889 －2894.NING Li-juan， XU Wei. Stochastic resonance under modulated noise in linear systems driven by dichotomous noise[J].Acta Physica Sinica，2009，58(5)，2889 －2894.

[6]靳艳飞，徐 伟，李 伟，等.具有周期信号调制噪声的线性模型的随机共振[J].物理学报，2005，54(6):2562－2567.JIN Yan-fei，XU Wei，LI Wei，et al.Stochastic resonance for periodically modulated noise in a linear system[J].Acta Phys.Sin.，2005，54(6):2562 －2567.

[7]徐 伟，靳艳飞，徐 猛，等.偏置信号调制下色关联噪声驱动的线性系统的随机共振[J].物理学报，2005，54(11):5027－5033.XU Wei，JIN Yan-fei，XU Meng，et al.Stochastic resonance for bias－signal－modulated noise in a linear system [J].Acta Phys.Sin.，2005，54(11):5027 －5033.

[8]周登荣，郭锋，鲁加国，等.乘性与信号调制噪声在线性模型中的随机共振[J].四川师范大学学报:自然科学版，2010，33(2):270 －272.ZHOU Deng-rong，GUO Feng，LU Jia-guo，et al.Stochastic resonance ofa linearmodelwith multiplicative signal modulation no ise [J]. JournalofSichuan Normal University:Natural Science，2010，33(2):270－272.

[9]周登荣，周玉荣.乘性噪声作用下线性模型中的随机共振[J].重庆师范大学学报:自然科学版，2008，25(3):70－73.ZHOU Deng-rong，ZHOU Yu-rong.Stochastic resonance of a linear model subject under mult iplicative noise[J].Journal of Chongqing Normal University:Natural Science，2008，25(3):70－73.

[10]蒋世奇，古天祥.随机振幅周期信号驱动的一阶线性系统的随机共振[J].电子测量与仪器学报，2008，22(1):104－108.JIANG Shi-qi，GU Tian-xiang.Stochastic resonance in first order linear system driven by random amplitude periodical signal[J]. JournalofElectronic Measurement and Instrument，2008，22(1):104 －108.

[11]Gitterman M.Classical harmonic oscillator with multiplicative noise[J].Physica A，2005，352(2 －4):309 －334.

[12]Gitterman M.Harmonic oscillator with multiplica－tive noise:nonmonotonic dependence on the strength and the rate of dichotomous noise [J].Phys.Rev.E，2003，67(5):57103/1－57103/4.

[13]蒋世奇，郭 锋，周玉荣，等.RC串联电路的随机共振[J].电子科技大学学报，2007，36(5):942 －944.JIANG Shi-qi，GUO Feng，ZHOU Yu-rong，et al.Stochastic resonance in an RC series circuit[J].Journal of University of Electronic Science and Technology of China，2007，36(5):942－944.

[14]郭 锋，周玉荣，蒋世奇，等.具有随机参数的线性振荡器的随机共振[J].计量学报，2008，29(3):267 －270.GUO Feng，ZHOU Yu-rong，JIANG Shi-qi，et al.Stochastic resonance in a linear oscillator with random parameter[J].Acta Metrologica Sinica，2008，29(3):267 －270.

[15]郭立敏，徐 伟，阮春蕾，等.二值噪声驱动下二阶线性系统的随机共振[J].物理学报，2008，57(12):7482－7486.GUO Li-min，XU Wei，Ruan Chun-lei， et al.Stochastic resonance for dichotomous noise in a second derivative linear system[J].Acta Physica Sinica，2008，57(12):7482－7486.