形状记忆合金梁在简谐和白噪声联合激励下的混沌及安全盆侵蚀现象

葛 根，竺致文，许 佳

(1.天津工业大学 机械工程学院，天津 300160;2.天津大学 机械学院工程力学系，天津 300072)

形状记忆合金梁的振动具有丰富的非线性动力学特性，研究其振动特性对研究形状记忆合金的工程应用具有重要的实用价值。比如，微型泵的形状记忆合金隔膜和形状记忆合金机械夹的振动，可当做形状记忆合金梁模型来处理。

目前对形状记忆合金的本构模型研究众多[1－7]，这些研究主要集中在热动力学理论，微观力学理论，相变理论等领域，而且这些本构模型的数学表达式多为符号函数或分段函数。因此基于这些模型的形状记忆合金构件的振动分析变得较为困难，从而学者们倾向于数值模拟多于理论分析。国内外学者近年来提出了众多关于形状记忆合金梁振动的研究成果。Collet等[8]在考虑了SMA的在拉、压和温度载荷中的对称性假设后，研究了形状记忆合金梁的动力学行为。Hashemi等[9]研究了在拉、压和温度加载中的非对称性假设下梁的自由振动和脉冲激励振动问题。Marcclo等[10]用数值方法研究了形状记忆合金双杆系统的同宿分岔和混沌现象。张清泉等[11－12]根据Machado本构模型建立了形状记忆合金梁的动力学模型并研究了其振动的稳定性和混沌现象。吴志强等[13]研究了形状记忆合金层合梁的非线性动力响应特性。葛根等[14]研究了简支形状记忆合金梁受简谐激励下的混沌阈值问题。这些研究集中在确定性系统范围内，而都没有研究随机激励对系统发生混沌的影响及激励幅值对系统安全盆的边界的侵蚀现象。

本文基于van-der-pol环模型模拟了形状记忆合金本构模型中的迟滞环特性。该模型为光滑函数，从而有利于理论分析。从该模型出发建立了受轴向简谐、横向白噪声联合激励下的形状记忆合金简支梁的振动模型。利用随机Melnikov过程法得出系统发生随机混沌的阈值必要条件。为了充分说明系统是否发生混沌，采用数值方法得到了系统安全域边界的侵蚀现象，发现激励幅值的变化导致安全盆内部出现分形结构，这是识别混沌的另一种有效而可靠的方法。这些结果对SMA梁的应用安全具有较大的实际意义。

1 形状记忆合金梁的振动模型

考虑一个矩形截面的简支Euler-Bernoulli形状记忆合金梁如图1所示。梁长为l，b为横截面宽度，h为梁高。中点的y方向位移为w。轴向受简谐激励N，形式为:N=p0+pcos(Ωt)，同时受施加在梁中点的面内横向随机激励Fη(t)，F为幅值，η(t)为标准高斯白噪声，具有零均值，强度为D。

因为形状记忆合金满足拉压条件下的应力应变关系的对称性[8]，故坐标中心可取为梁横截面的几何中心处。

图1 简支形状记忆合金梁的模型及坐标Fig.1 The model and the coordinate of the simply supported SMA beam

假设该梁为小挠度梁，其动力学方程为:

其中:c表示线性阻尼，ρ表示梁的密度，A为梁的横截面积，M为梁的弯矩，w为中点横向位移，该两端简支梁的边界条件可表示为:

满足振动边界条件的一阶模态为:

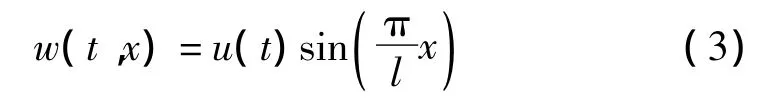
考虑小挠度梁的几何变形条件:

可得弯矩的表达式为:

根据文献[8]中的等应变加、卸载实验数据可知，在不考虑温度变化时，形状记忆合金的加载－卸载应力应变曲线有明显的滞后环特性。为模拟这一特性并使函数形状光滑以利于后续分析，可考虑建立一个由关于原点对称的vanderpol环加上一条骨架曲线形式的模型。

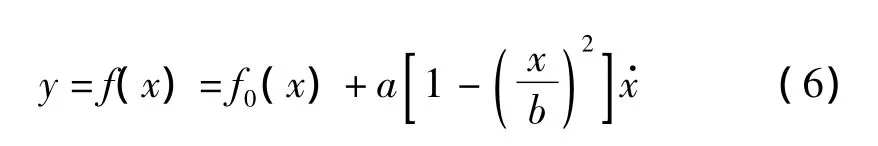
其中:f0(x)为迟滞环的骨架曲线;参数a，b表示骨架曲线和实验应力应变曲线之间的偏差。假设应力－应变环的对称中心为G(ε0，σ0)，则SMA的应力－应变关系可表示为:

可展开为:

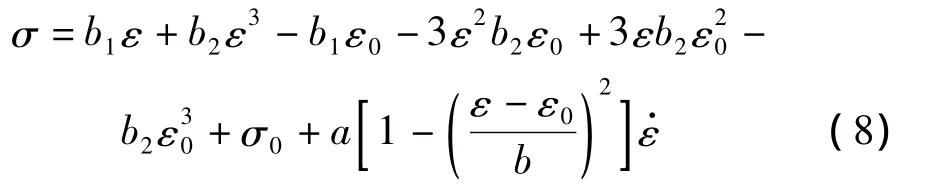
考虑到当ε=0时，加载和卸载曲线的对应应力值必需相等，且此时SMA应没有残余应力，故模型参数应满足由此可得形状记忆合金的应力应变最终函数关系为:

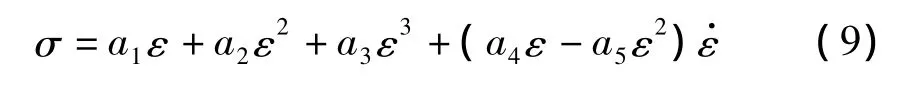
其中:

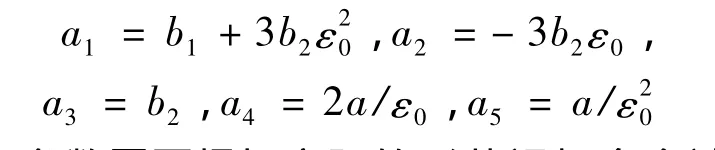
以上参数需要根据实际的形状记忆合金试件的实测数据来确定。

把式(3)、(4)代入式(9)可得应力和位移w的关系后，再代入式(5)得弯矩表达式:

其中:I1=bh3/(12l2)，I3=bh5/80l6。

把式(3)、(10)代入式(1)并积分可得单自由度常微分形式的梁动力学非线性振动方程如下:

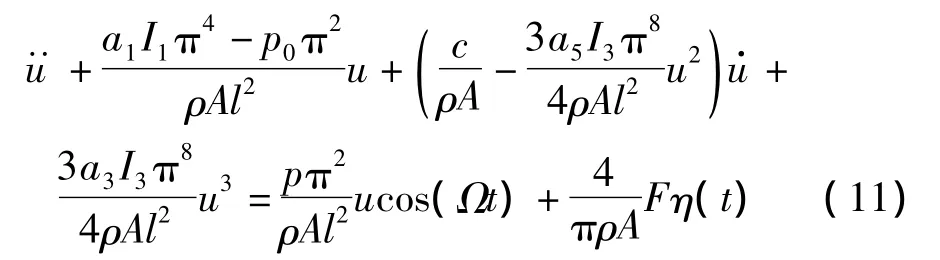
为了便于后续的非线性分析和揭示更丰富的系统可能存在的动力学现象，对式(11)作如下无量纲变化:并略去上标:

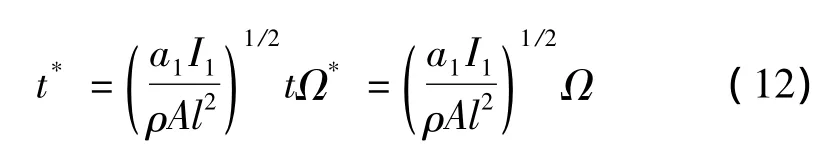
模型(11)可变形为如下无量纲形式:

其中参数为:

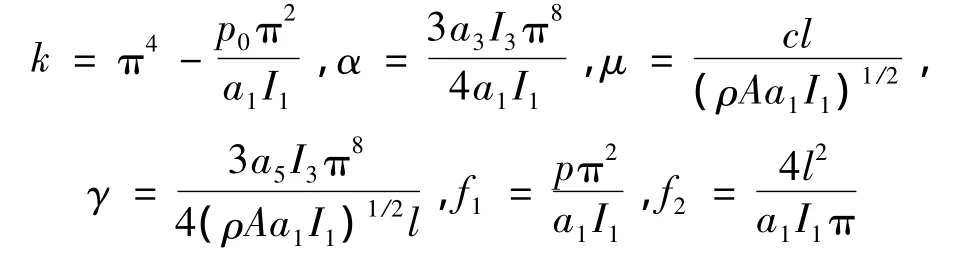
本文中考虑静态载荷p0大于极限屈曲载荷，即线性刚度k为负(屈曲)的情况。对模型(13)引入如下尺度变换:可得:

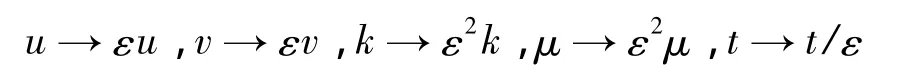
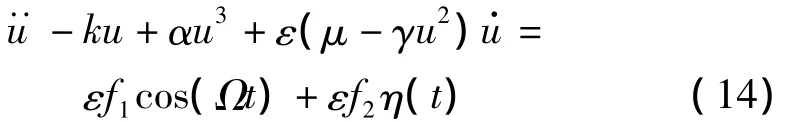
2 均方意义下Melnikov过程

根据文献[15]，一个受弱噪声激励的弱阻尼单自由度Hamilton系统可表示为:

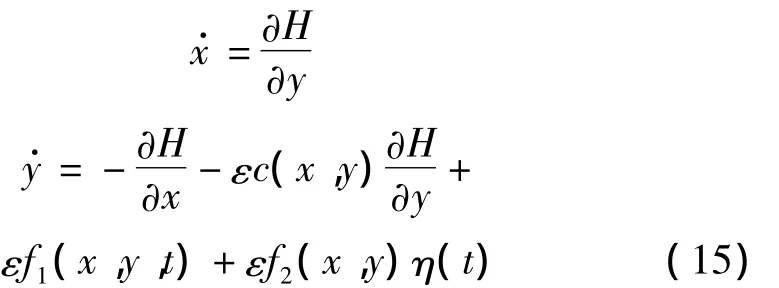
其中:x，y为广义位移和广义动量，H为广义能量，c(x，y)为阻尼项，f1(x，y，t)为确定性激励项，f2(x，y)为随机激励项系数，η(t)为白噪声信号。

Melnikov方法是一种通过判断系统的稳定流形和不稳定流形距离为零来判断混沌的有效方法，它要求系统的激励为连续且有界。由于η(t)对任意时间t1和 t2，取任意常数 δ1＞0，令|η(t1)－ η(t2)|＜ δ1，则必存在一个常数δ2＞0使|t1－t2|＜δ2存在。由此可近似认为η(t)是连续且有界的，所以满足Melnikov方法适用的前提假设。

根据Wiggins[16]提出的系统随机Melnikov过程可表示为:

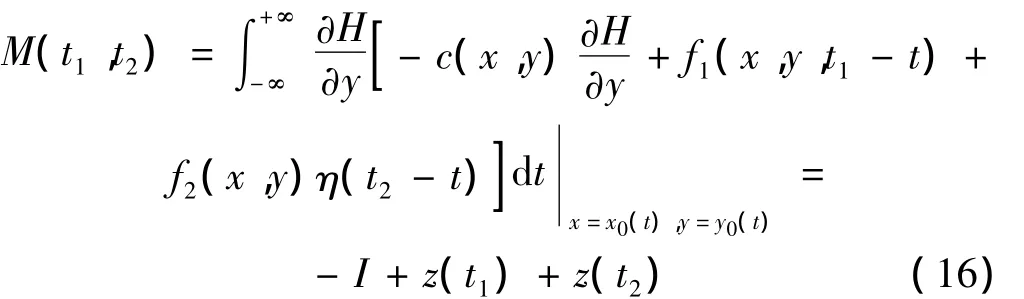
其中:x0(t)，y0(t)为系统(15)未扰时的同宿轨道表达式。

积分中的前两项－I和z(t1)分别为阻尼项和确定性激励项的随机Melnikov积分的均值，第三项z(t2)表示由于随机项引起的Melnikov过程积分。

把系统(14)式可变形为式(15)的形式，以便于后续处理。式(14)的系统Hamilton函数(广义能量)为:，代入式(15)得:

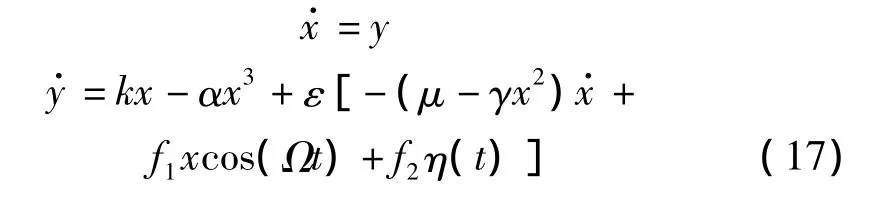
显然系统(17)的未受扰系统存在鞍点(0，0)，从鞍点出发围绕两个中心的系统的同宿轨道Γ0(t)={Γ0－(t)|·|t∈R}可表示为:把式(18)，式(19)代入式(16)可得系统确定性部分的Melnikov积分表达式为:

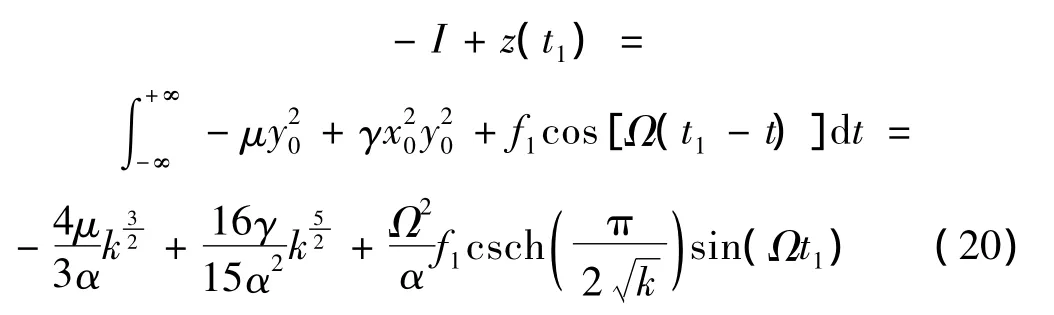
为便于计算式(16)中的z(t2)，可认为:

z(t2)=是系统随机输入η(t)通过一个线性滤波器后的脉冲响应函数，其傅里叶变换为:

其中:Sη(ω)为白噪声的谱密度。对白噪声而言，谱密度为一个常数

从能量的角度[17]如此可得均方意义上系统可能发生随机混沌的判据为:

本文中取参数值为:

代入式(20)、(21)可得:

把式(25)代入式(23)后数值积分，可得:

则满足式(23)的激励幅值f1，f2条件为:

不等式(23)是发生随机混沌的必要条件，但并不是发生随机混沌的充分条件。下面内容将通过研究系统安全盆的分形现象来判断系统混沌。

3 随机安全盆的侵蚀现象

系统发生混沌时，稳定流形和不稳定流形将发生横截相交，在相平面内盘旋缠绕成复杂结构，某些初始点出发的相轨线将穿出系统的安全域边界，从而导致系统的不安全，这种现象在很多文献中称为安全盆的侵蚀现象。很多时候系统的安全盆受到侵蚀时，相轨线不断逃逸出安全盆，并再回到安全盆内，因此安全盆边界将呈现分形形状，而安全盆的分形边界是产生混沌的一个重要判据[18]。

为了研究系统的激励对安全盆的影响，首先在相平面内描绘一个包含未扰系统安全盆的区域G。

其中:H为系统的总能量上限，取H=0.1(图2)。把区域G划分为步长h=0.002的小格子，把每个小格子作为系统的初值，当某个初值在时间步长为0.01，迭代计算2×105次后仍然留在安全盆内，可认为该初值是安全的。随机输入采用蒙特拉罗法模拟，依次使用12组不同的白噪声，只有当该初值在全部12组白噪声激励下都是安全的，才能记录这个初值点，否则认为该初值是不安全的，在安全盆中删除。

图2 无扰系统的安全盆(H=0.1)Fig.2 The safe basin of the system(H=0.1)

当先不加随机激励时，增大确定性激励幅值，观察系统安全盆的形状变化如图3所示。

图3(a)显示，随着确定性激励满足混沌判据(27)式，使系统的发生混沌，系统安全盆的边界受到侵蚀，随着激励幅值f1增大，系统安全盆的内部出现分形的情况更明显，如图3(b)显示。安全盆的内核部分(未扰系统的两个中心附近)仍然是绝对安全的，而外围部分区域就不能保证绝对安全。如图3(c)显示，即使系统在随机外激励作用下显示出振动的随机性，但是并没有激发出系统内在的随机行为(混沌)，则安全域的边界仍为光滑的。

当随机信号和简谐激励联合作用后，仍取满足式(27)的激励幅值f2，安全盆的侵蚀情况如图4所示。

比较图3(a)和图4(a)可知，随机信号的加入使安全盆内部的安全点减少了，原来的平滑边界也出现了分形。图4(a)和图4(b)的比较可知，加入的随机激励幅值变大后，安全盆内核部分的安全性变化不大，但是外围区域的层状分形结构变得十分明显。而比较图3(b)和图4(c)可知，确定性激励较大时，随着随机激励的加入，安全盆内核安全区域仍几乎不变，但是原来图3(b)中的外层分形区几乎全部消失。这一现象对SMA梁结构的实际应用具有一定的理论指导意义，实际的SMA梁的尺度一般较小，那么结构受到环境随机干扰(热噪声，电磁噪声)的影响就不能被忽略，为了使振动系统能够“健康”地工作，在选择系统的“初态”时应该只能选定为图4(c)中的区域。图4(c)和图4(d)的比较可知，随着随机激励幅值的进一步增大，安全盆的内核部分也逐步开始被侵蚀，分形结构逐步变得明显。

图3 简谐激励或噪声激励下的安全盆Fig.3 The safe basin of the system under harmonic excitation or noise excitation

图4 同时受简谐和白噪声联合激励时的安全盆Fig.4 The safe basin of the system under both harmonic and white noise excitations

图5 时间历程和相图Fig.5 Time series and phase portrait

混沌的一个典型特征是对初值的极端敏感依赖，为了进一步说明安全盆的侵蚀现象，观察不同的初值点所形成的时间历程和相图如图5所示。

图5(a)显示系统做混沌运动，图5(b)显示一种概周期运动，图5(c)显示的是在随机激励下的随机运动。图5(a)、(b)两图显示在同一组激励下，不同初值导致的运动不同，说明了有的运动能穿出安全域边界，有的则不能，结合图4(d)说明安全盆内部出现了分形特性。图5(c)对应图2(c)说明了即使系统在单纯的随机因素激励下出现了振动的随机特性，但是系统没有发生混沌，则安全盆不会出现分形边界。

4 结论

本文通过建立形状记忆合金的连续光滑应力－应变模型后得到了简支SMA梁的动力学模型，化简后振动方程为一个具有负刚度的杜芬－范德坡模型，该模型受简谐参激和白噪声外激励联合作用。随机Melnikov过程的计算给出了该系统发生混沌的必要条件判据。数值模拟了系统出现混沌时安全盆的边界会出现分形特征。本文的工作意义主要体现在:

(1)通过计算系统发生混沌的激励幅值条件为SMA梁的稳定工作提供了理论参考。安全盆的边界分形给判断混沌提供了除Melnikov方法之外的依据。

(2)安全盆可以清晰的判断初值对系统稳定运行的意义，尤其在施加了噪声干扰后，系统能够安全工作的初值会减少，此研究意义在于:系统在较大激励幅值下即使发生混沌，只要把初值取在安全盆内的安全区，系统的能量也不会超出许可限制。为系统的健康工作提供了参考依据。

[1]Tanaka K.A thermomechanical sketch of shape memory effect:one-dimensional tensile behavior [J]. Res Mechanics，1986，18:251 －263.

[2]Liang C，Rogers C A.A one-dimensional-thermo mechanical constitutive relation of shape memory materials[J].Journal of Intelligent Material System Structure，1990，1:207 －234.

[3]Boyd J G，Lagoudas D C.A thermodynamical constitutive model for shape memory materials[J].International Journal of P1asticity，1996，12:805 －873.

[4]Brinson L C.One-dimensional constitutive behavior of shape memory alloys:thermomechanical derivation with nonconstant material functions and redefined martensite internal variable[J].Journal of Intelligent Material Systems and Structures，1993，4:229 －242.

[5]Graesser E J，Cozzarelli F A.A proposed three-dimensional constitutive model for Shape memory alloys[J].Journal of Intelligent Material Systems and Structures，1994，14:78－89.

[6]Ivshin Y，Pence T J.Thermomechanical model for a one variant shape memory material[J].Journal of Intelligent Material Systems and Structures，1994，5:455 －473.

[7]Auricchio F，Lubliner J.Uniaxial model for shape-memory alloys[J].International Journal of Solids and Structures，1997，34:3601 －3618.

[8]Collet M，Foltete E，Iexcellent C.Analysis of the behavior of a shape memory alloy beam under dynamical loading[J].European Journal Mechanics，A-Solids，2001，20:615 － 630.

[9]Hashemi S M T，Khadem S E.Modeling and analysis of the vibration behavior of a shape memory alloy beam [J].International Journal of Mechanical Sciences，2006，48(1):44－52.

[10]Savi M A，Pacheeo P M，Braga M B.Chaos in shape memory two-bar truss[J].InternationalJournalofNon-Linear Mechanics，2002，37(1):1387 －1395.

[11]李映辉，张清泉.形状记忆合金梁动力稳定性[J].西南交通大学学报，2005，40(4):453 －456.

[12]张清泉，李映辉，姚 进.形状记忆合金梁动力稳定性及混沌运动[J].四川大学学报(工程科学版)，2004，36(5):30－36.

[13]Wu Z Q，Zhang Z H.Force displacement characteristics of simply supported beam laminated[J].Acta Mech.Sin，2011，27(6):1065－1070.

[14]葛 根，王洪礼，许 佳.形状记忆合金梁的建模及混沌阈值计算[J].振动与冲击，2012，31(12):103－107，119.

[15]Liu Z H，Zhu W Q.Homoclinic Bifurcation and Chaos in simple pendulum under bounded noise excitations[J].Chaos，Solitons and Fractals，2004，20:593 －607.

[16]Wiggins S.Global bifurcations and chaos:analytical methods[M].New York:Springer，1988.

[17]Lin H，Yim S C S.Analysis of a nonlinear system exhibiting chaotic，noisy chaotic，and Random behaviors[J].J.Appl Mech ASME，1996，63:509 －516.

[18]Gan C B.Noise induced chaos in a quadratically nonlinear oscillator[J].Chaos，Solitons ＆ Fractals，2006，30:920－929.