圈的强刺图的最优Pebbling数

宁鹏祥，叶永升

(淮北师范大学 数学科学学院，安徽 淮北 235000)

圈的强刺图的最优Pebbling数

宁鹏祥，叶永升

(淮北师范大学 数学科学学院，安徽 淮北 235000)

图 G上的一个pebbling移动是从一个顶点处移走两个pebble，而把其中的一个移到与其相邻的一个顶点上.图 G的最优pebbling数 f'(G)是指最小的整数 p，满足从 G的 p个pebble的某种放置方式开始，总可以通过一系列的pebbling移动把一个pebble移到 G的任一个顶点 v上.文章主要研究圈的强刺图C的最优pebbling数.

最优pebbling数;α－pebbling;强刺图

0 引言

图的pebbling问题首先是由Chung[1]所讨论的.图 G的pebbling数 f(G)第一次是由Saks和Lagarias[1]提出并研究的，在此基础上，Lemke和Kleitman[2]解决了一个数论问题，而最优pebbling数是由Pachter等[3]介绍的.

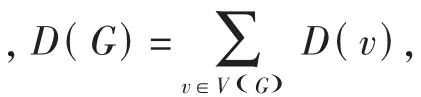
定义1 设 p1，p2，…，pn为非负整数，G是顶点数为 n的图，在图 G的每个顶点 ui处连接 pi个度为1的点，这里的 i=1，2，…，n，这样构成的图称为图 G的刺图，记作 G＊.若 pi≥1(i=1，2，…，n)，那么这样构成的图称为图 G的强刺图，记作 G＊＊.称度为1的所有点为 G＊＊的悬空点，以悬空点为端点的所有边称为G＊＊的刺.

设 Cn=(v1，v2，…，vn)，在 vi上加 pi(pi≥1)个悬空点得到的新图为 Cn的强刺图C.在本文中，对于v∈V(Cn)，在 Cn上去掉点 v所得的图表示为 Cn－1.

1 定理及证明

为证明本文的定理，先介绍下面的引理和推论.

由引理2可得到下面一个结论.

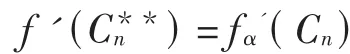
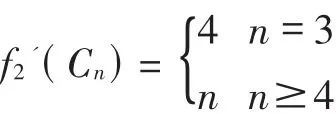
当 n=3时，设 D为 C3的一个分布，且满足 D(v1)=4，D(v2)=D(v3)=0，那么 C3通过一系列的pebbling移动，任意一点都能获得至少2个pebble，从而f2'(C3)≤4.若 D(C3)=3，那么无论怎么分布，C3通过一系列的pebbling移动，至少有一点至多只能得到1个pebble.故f2'(C3)=4.

当 n=4时，设 D为 C4的一个分布，且满足 D(v1)=D(v3)=2，D(v2)=D(v4)=0，那么 C4通过一系列的pebbling移动，任意一点都能获得至少2个pebble，从而f2'(C4)≤4.因为f2'(C4)≥f2'(C3)，从而f2'(C4) =4.

当 n≥5时，在 Cn上构造一个最优可解的分布 D，且|D|=n.令 n=3 t+r，当1≤i≤3 t时，设 D(vi)= 2这里 i≡2 mod 3，D(vi+1)=1，D(vi－1)=0.如果 r=1时，令 D(v3t+1)=1，如果 r=2时，令 D(v3t+2)=2且 D(v3t+1)=0，所以f2'(Cn)≤n.下证f2'(Cn)=n.

假设 n为最小的整数使f2'(Cn)＜n.在 Cn上构造一个最优可解的分布 D，且|D|=n－1.修改 D得到D＊，使得 D＊是 Cm(m＜n)上的一个最优可解的分布，且|D＊|＜m，从而得到矛盾.

(1)Cn中存在一个点 vi，使 D(vi)=1(1＜i＜n)(否则重新编号).

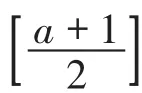
(2)Cn上每个放pebble的顶点上都放2个pebble.

在 Cn上一定存在相邻的3个顶点 vi，vi+1，vi+2，D[vi，vi+1，vi+2]=[2，0，2]或 D[vi，vi+1，vi+2]=[2，2，0].否则就有两个连续的没有分配到pebble的顶点，那么通过一系列的pebbling移动这两个顶点最多只能得到1个pebble，因此这样相邻的3个顶点一定存在.去掉 vi+1，vi+2和它们上面的pebble，从而得到 Cn－2上的一个新的分布 D＊，在分布 D＊下，vi+3是放有2个pebble或能从 vi上得到1个pebble，因此 vi+3在分布D＊下通过一系列的pebbling移动得到的pebble的个数不小于在分布 D下通过一系列的pebbling移动得到的pebble的个数，在分布 D和分布 D＊下，vi－1和 vi+4通过一系列的pebbling移动得到的pebble数一样，从而 D＊是最优可解的.由于|D＊|＜n－2，故f2'(Cn－2)＜n－2，矛盾.

(3)Cn包含一顶点 vi，满足 D(vi)≥3.

综上所述，这样的 n是找不到的，从而当 n≥5时，f2'(n)=n.

[1]CHUNG F R K.Pebbling in hypercubes[J].SIAM JDiscrete Math，1989，2(4):461－472.

[2]LEMKE P，KLEITMAN D.An addition theorem on the integersmodulon[J].JNumber Theory，1989，31(3):335－345.

[3]PACHTER L，SNEVILY H，VOXMAN B.On pebbling graphs，Proceedings of the Twenty－sixth Southeastern International Conference on Combinatorics，Graph Theory and Computing[J].Congeessus Numerantium，1995，107(3):65－80.

[4]HUNG L F，CHIN L S.The optimal pebbling number of the complete m－ary tree[J].Discrete Math，2000，22(2):89－100.

[5]MOEWSD.Optimally pebbling hypercubes and powers[J].Discrete Math，1998，190(4):271－276.

[6]ALPAY Kirlangic.The scattering number of thorn graphs[J].International Journal of Computer Mathematics，2004，81(3):299－311.

Abstract:The pebbling move of G is taking two pebbles off one vertex and then placing one on an adjacent vertex.The optimal pebbling number of G，f'(G)，is the least positive integer p such that p pebbles are placed suitably on vertices of G and for any target vertex v of G.In this paper，we find the optimal pebbling number of the circle of strong thorn graphs.

Key words:optimal pebbling number;α－pebbling;strong thorn graphs

The Optimal Pebbling Number of the Circle of Strong Thorn Graphs

NING Peng－xiang，YE Yong－sheng
(School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China)

O 157.5

A

2095－0691(2012)03－0015－03

2012－01－14

安徽省自然科学研究项目(2010SQRL136ZD，1208085QF119)

宁鹏祥(1985－ )，男，安徽太和人，硕士生，研究方向为图论及其应用.通讯作者:叶永升(1964－ )，男，安徽嘉山人，副教授，研究方向为图论及其应用.