类氢离子电离能相对论性计算的改进

马 堃，褚 园，黄时中

(1.黄山学院信息工程学院,安徽黄山245041；2.安徽师范大学物理与电子信息学院，安徽芜湖241000)

类氢离子电离能相对论性计算的改进

马 堃1，褚 园1，黄时中2

(1.黄山学院信息工程学院,安徽黄山245041；2.安徽师范大学物理与电子信息学院，安徽芜湖241000)

在考虑了核运动的情况下，给出了以相对论动力学方程为基础的类氢离子电离能的计算公式，对实验上已观测到的37个类氢离子的电离能进行了计算，结果与实验值的误差远小于玻尔理论或量子力学理论的误差，并优于文献中的计算结果。

类氢离子；电离能；相对论性理论

0 引言

类氢离子的电离能是原子物理、天体物理、等离子体物理和材料物理等领域中常用的重要参数，而目前在实验上只观测到了37个类氢离子的电离能，因而提高其理论计算精度是很有必要的。玻尔理论[1-3]虽然是一个半经典半量子的理论，但由此得到的类氢离子的电离能的计算公式与用量子力学理论[4]所得到的公式完全相同，这类公式的一个明显缺陷是随着原子序数Z的增大，电离能的理论计算值与实验观测值的误差不断增大。相对论Dirac-Fock自洽场方法[5]，虽然计算精度较高，但此方法很繁杂，且计算数据有限。最弱受约束电子势模型(WBEPM)方法[6-7]，这种方法虽然计算精度高，但依赖于一定的实验数据。2010年，黄时中等给出了以相对论动力学方程取代牛顿力学方程而形成的相对论性玻尔类氢离子理论，在此基础上给出了类氢离子电离能的相对论性计算公式，对实验上已观测到的37个类氢离子的电离能进行了具体计算[8]，但文中忽略了氢原子核的运动，本文将在此基础上，考虑相对论效应和核运动的情况，改进了类氢离子电离能的相对论性计算公式，对实验上已观测到的类氢离子电离能进行了计算，计算结果与实验值的误差远小于玻尔理论或量子力学理论的误差，并优于文献[8]的计算结果。

1 相对论性玻尔类氢原子理论

按照玻尔理论，类氢原子中电子沿圆轨道绕原子核的运动，如图1所示。

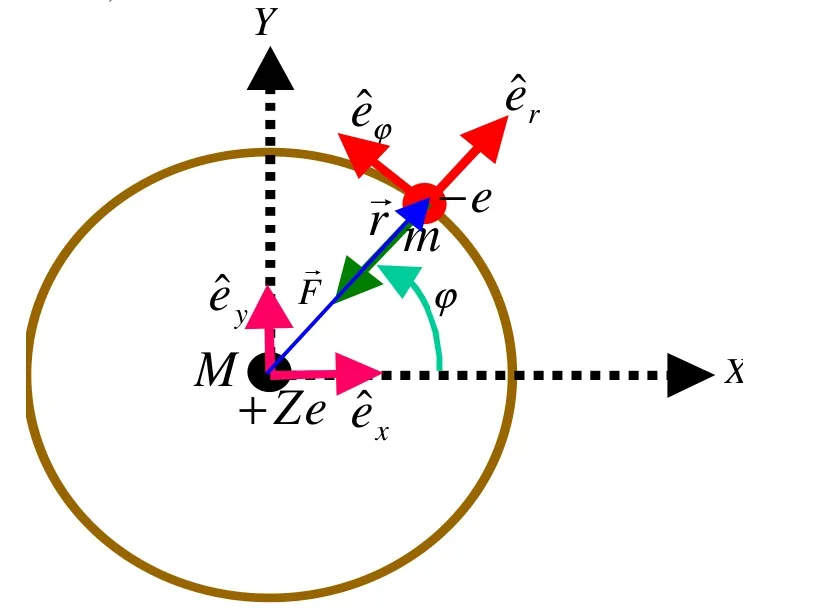
图1 类氢原子的玻尔模型

其运动满足牛顿力学方程：

考虑到相对论性效应，则玻尔理论中所用的牛顿力学方程(1)改为相对论动力学方程

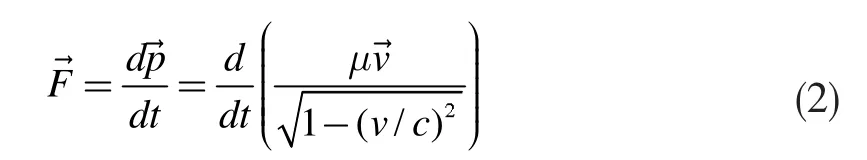
根据角动量量子化条件，电子以速率v在半径为r的圆周上绕核运动时，只有电子的角动量等于ħ的整数倍的那些轨道才是稳定的，即

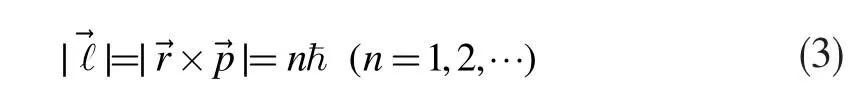
从上式可以看出，电子的速率必须是与时间无关的常量，否则电子的角动量将与时间有关，则角动量量子化条件(3)不能满足，所以相对论动力学方程(2)可以进一步化简为

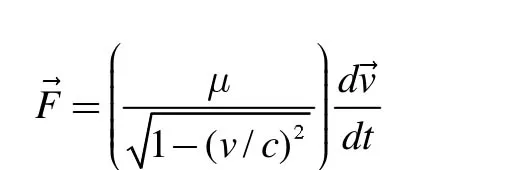
又因为匀速率圆周运动的加速度为

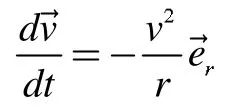
因此，我们有

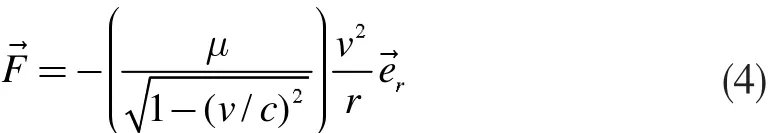
另一方面，电子所受的库仑力为

由以上两式，我们得到电子绕核作圆周运动的过程中速率v与半径r的关系

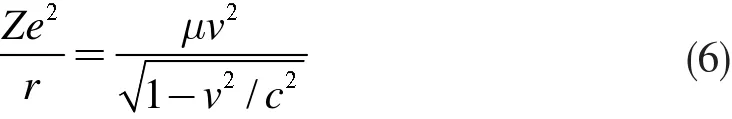
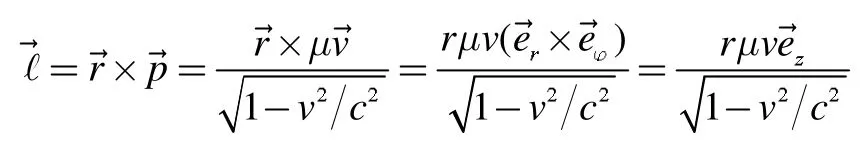
即

利用角动量量子化条件(3)消去半径r，我们得到

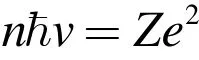
即类氢原子中电子绕核作圆周运动的速率为

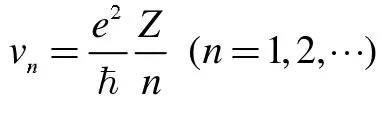
或者

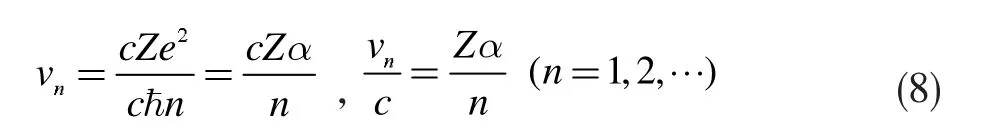
现在，我们用相对论理论来分析类氢原子系统的总能量。根据相对论理论，氢原子系统的总能量为

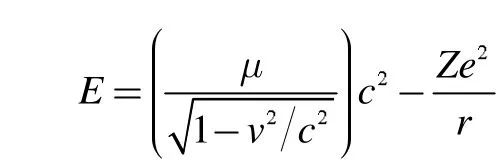
利用式(6)和(8)，进一步有

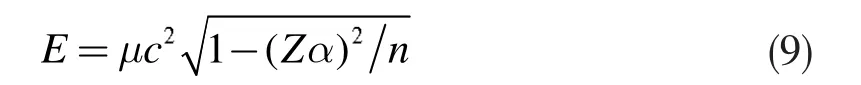
从上式中减去静止能量，得到相对论下类氢原子系统的能级表达式

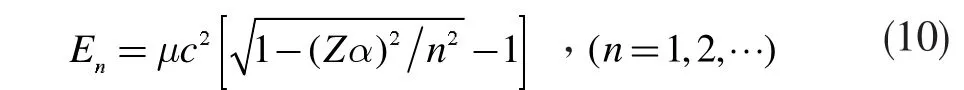
对于第一轨道(n=1)，

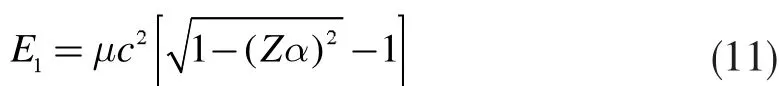
类氢原子系统的电离能为

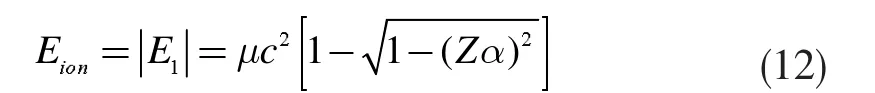
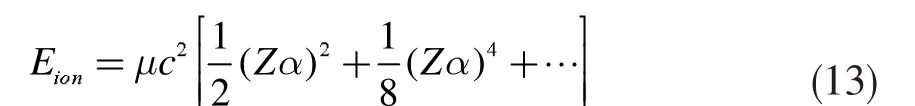
其中第一项等于用玻尔理论或者量子理论所得到的类氢原子系统的电离能[4]

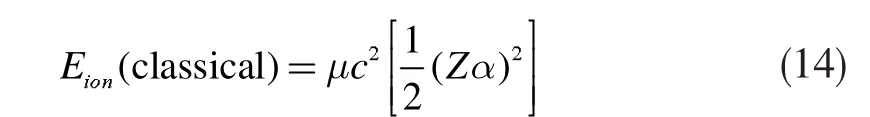
3 应用及总结

下面分别用式(14)和(12)对Z=1-37的类氢原子系统的电离能进行计算，结果列于表1，表中同时列出了类氢原子电离能的实验观测值。[9]

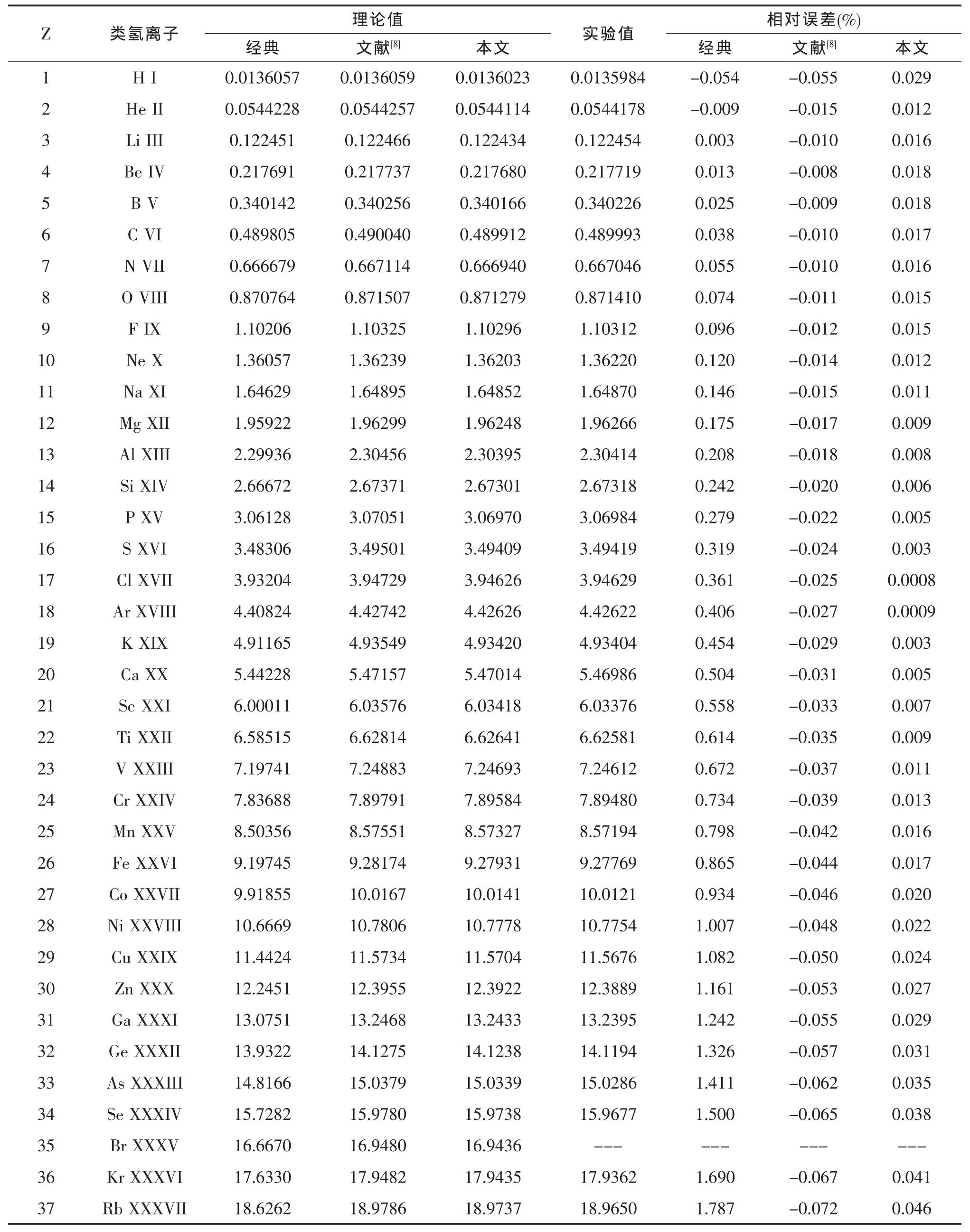
表1 类氢原子系统的电离能[单位：Kev]

由表1可以看出，通过本文模型进行计算的37个类氢离子的电离能，精度得到了全面的提高。特别地，如：Cl XVVII和Ar XVIII精度提高了近97%。这说明，本文建立的计算模型是有效的，且比相对论Dirac-Fock自洽场方法简单得多，而与最弱受约束电子势模型(WBEPM)方法相比，本方法不依赖于实验数据。

为更加直观的观察本文计算结果与经典模型和文献[8]计算结果的比较，我们采用了MATLAB软件绘制了3种计算模型下类氢原子系统的电离能的计算误差随核电荷数的变化情况，如图2所示，图中的曲线表示实验值，为突出误差，在作图时，将误差扩大了50倍，横坐标是核电荷数，纵坐标是能量，单位为kev。从图2中可以看出，1，2的误差随着核电荷数的增加呈单向的递增趋势，而3的误差随着核电荷数的增加呈螺旋式变化，特别地，在Z=17和10时，几乎与实验值相同。

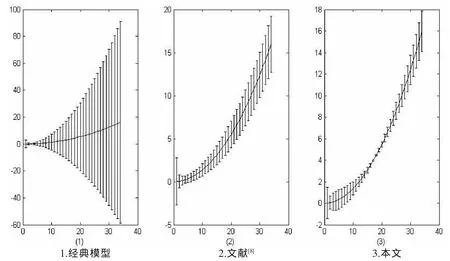
图2 三种计算模型下类氢原子系统的电离能的计算误差随核电荷数的变化

[1]Bohr Niels.The binding of electrons by positive nuclei[J].Phil.Mag,1913,26:1-25.

[2]Bohr Niels,Systems containing only a single nucleus[J].Phil.Mag,1913,26:476-502.

[3]Bohr Niels.Hydrogen and helium spectra[J].Nature,1913,95:231-232.

[4]曾谨言.量子力学卷Ⅰ(第一版)[M].北京:科学出版社,1990:270-283.

[5]安兴泰，周忠源，潘守甫.“水窗”波段类锂离子各电离态的电离能[J].原子与分子物理学报，1994，11(3):327-329.

[6]郑能武.关于多电子原子及离子体系的一种新的理论模型[J].科学通报，1985，30(3):1801-1804.

[7]张学龙，张国营，相邻类氢离子电离能关系的研究[J].原子与分子物理学报，2004，21(3):529-531.

[8]黄时中，李淑贞，褚进民.类氢离子电离能的相对论性计算[J].安徽师范大学学报，2010，33(2):121-124.

[9]NIST Atomic Spectra Database.Energy Levels Data[DB].National Institute of Standards and Technology.2001.09.09[2006.05].http://physics.nist.gov/cgi-bin/AtData/display.ksh.

责任编辑：胡德明

Abstract:Taking nuclear movement into consideration,this paper puts forward a relativistic calculation formula for ionization energy of hydrogen-like ions based on relativistic dynamical equations.The ionization energy of 37 types of hydrogen-like ions observed in experiments is calculated with the formula.The experimental results show that the error is much smaller than that based on the Bohr Theory or Quantummechanical Theory,and better than the calculations found in the literature.

Key Words:hydrogen-like ions;ionization energy;Relativistic Theory

Improvement on the Calculation of Relativistism of Ionization Energy in Hydrogen-like Ions

Ma kun1,Chu Yuan1,Huang Shizhong2
(1.School of Information Engineering,Huangshan University,Huangshan245041,China;2.School of Physics and Electrical Information,Anhui Normal University,Wuhu241000,China)

O561.3

A

1672-447X（2012）03-0029-004

2011-11-26

安徽省教育厅自然科学研究项目(KJ2011Z363);安徽省高校2010年质量工程项目(20100990);安徽省教育厅自然科学研究项目(KJ2007B 029);黄山学院自然科学研究项目(2010xkj013)

马堃(1983-),安徽六安人,黄山学院信息工程学院讲师，硕士,研究方向为理论物理学。