一类非线性方程组正解的存在性
2012-09-12胡玲
胡 玲
(黄山学院数学与统计学院,安徽黄山245041)
一类非线性方程组正解的存在性
胡 玲
(黄山学院数学与统计学院,安徽黄山245041)
研究了一类非线性二阶常微分方程组m-点边值问题的正解存在性,在合适的条件下,运用抽象的不动点定理,得出了正解及多重解的存在性。
m-点边值问题;格林函数;锥
1 引言
近年来,常微分方程的边值问题在数学及工程科学中受到很大的关注,据我们所知,绝大多数结果都是针对单个方程及简单的边值条件的,例如:[1,2]
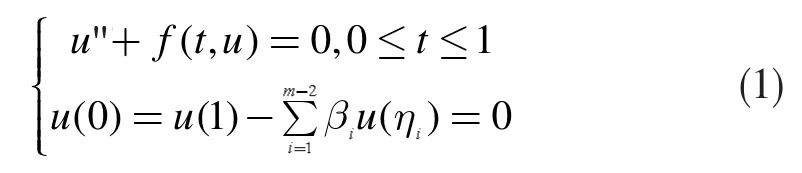
运用锥的不动点定理,可以获得(1)的正解存在性。再看下面的方程组:
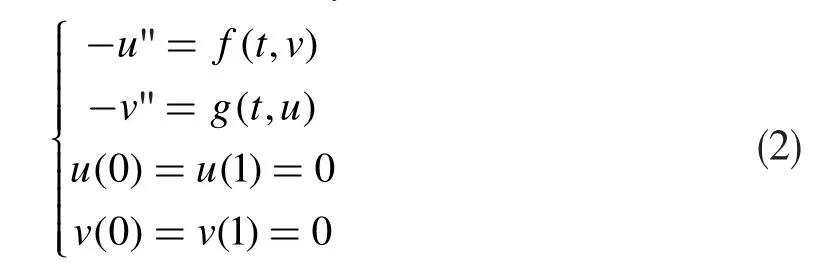
运用度理论[3],(2)的正解也可以获得,类似还有很多结果[4-6]。可以看到,(1)中只有单个方程,而(2)中的边值条件是最简单的。
结合(1)与(2),本文研究的是如下方程组:
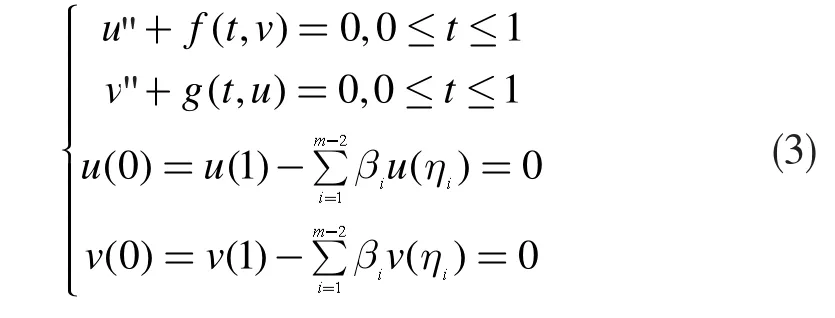
为了得到(3)的解的存在性,我们要用到格林函数,并定义一些锥,最后通过不动点定理得出正解的存在性及多重性。
2 引理
显然,方程组(3)可以转化为如下积分方程组:
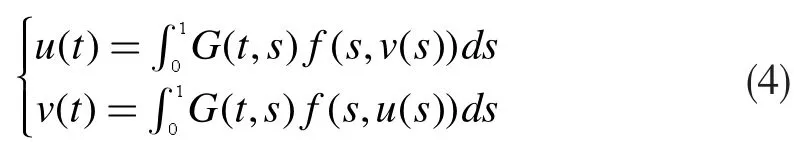
其中G(t,s)为格林函数,积分方程组(4)又可以化为非线性积分方程:

引理1:格林函数G(t,s)为如下形式:
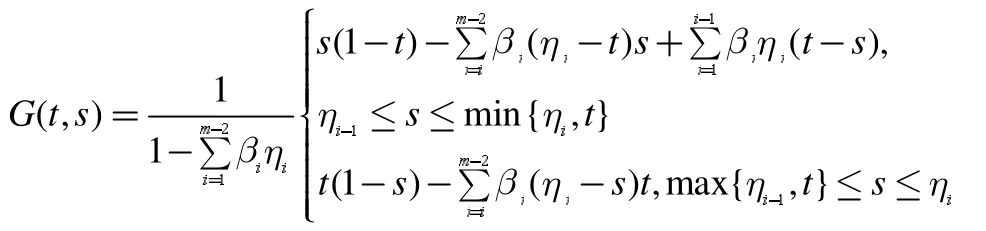
其中i=1,2,…m-1,显然,G(t,s)>0,G(0,s)=G(1,s)=0。

设m=min∫G( t, s) ds, M=max∫G( t, s) ds,显然,M>m>0。
设E=C[0,1],∀u∈E,定义u=maxu,那么{E,||·||}是一个巴拿赫空间,定义
K={u∈E u( t)≥0,minu( t)≥γu,η≤t ≤1},
显然K是E中的一个正锥。
由α(u)=minu( t ),我们定义函数α:K→R。定义算子
Tu( t)=∫G( t, s) f( s,∫G( s,σ)g(σ,u(σ))dσ)ds, u∈K,(6)由以上讨论可知,(3)的正解的存在性可以转化为算子T的正不动点的存在性问题。
3 定理
定理1:设a,b,c>0,满足a<b≤min{γ,m }c,f( t,0)≠0,g( t,0)≠0且M

那么边值问题(3)至少有3个正解u1,u2,u3,满足
证明:T如上定义,∀Ω∈K ,开集且非空,我们容易知道T:→K是全连续的。设
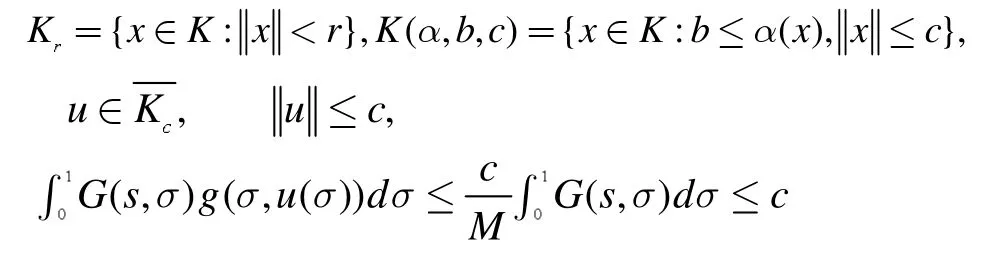
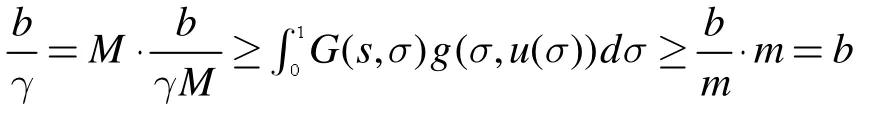
所以,我们有
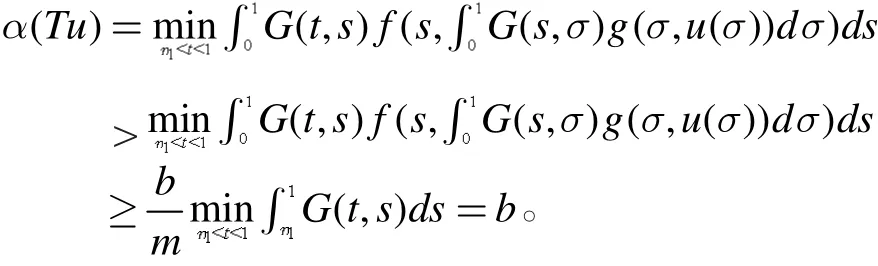
综上所述,锥压缩锥拉伸不动点定理的条件得到满足,我们得到至少有3个不动点u1,u2,u3,满足,即是边值问题(3)的3个正解。
[1]Guo Y,Ge W,Three positive solutions for second order m-point boundary value problems[J].Appl Math.Camp,2004,156(3):733-742.
[2]Guo Y,Ge W.Positive solutions for second order mpoint boundary value problem[J].Comp.Appl.Math,2003,151:415-424.
[3]Hu Ling and L.L.Wang,Multiple Positive Solutionsof Boundary Value Problems for Systems of Nonlinear Second-Order Differential Equations[J].Journal of Mathematical Analysis and Applications,2007,335:1052-1060.
[4]K.Deimling,Nonlinear Functional Analysis[M].Springer-Verlag,Berlin 1985.
[5]Leggett R W,Williams L R,Multiple positive fixed solutions of nonlinear operators on ordered Banach spaces[J].Indiana Univ.Math,1979,673-688.
[6]杨志林,孙经先,非线性二阶常微分方程组边值问题的正解[J].数学学报,2004,47(1):111-118.
责任编辑:胡德明
Abstract:The paper is concerned with positive solutions to m-point boundary value problems of a class of nonlinear second order differential equations.Under suitable conditions,the existence of positive solutions and multiplicity of solutions are proved by using abstract fixed-point theorems.
Key words:m-point boundary value problem;Green's function;cone
Positive Solutions of m-Point BVPs for Nonlinear Differential Equations
Hu Ling
(School of Mathematics and Statistics,Huangshan University,Huangshan245041,China)
O175.8
A
1672-447X(2012)03-0004-002
收搞日期:2012-03-21
安徽省教育厅教学研究项目(20100996);黄山学院质量工程项目(2011JPKC06)
胡玲(1981-),安徽黄山人,黄山学院数学与统计学院讲师,硕士,研究方向为微分方程。
