《代数学辞典》中译本初探

闫晓民

（内蒙古师范大学科学技术史研究院，内蒙古呼和浩特010022）

《代数学辞典》中译本初探

闫晓民

（内蒙古师范大学科学技术史研究院，内蒙古呼和浩特010022）

《代数学辞典》一书的翻译出版，在我国产生了重大的影响。本文比较分析了在日本和中国的出版背景，并对原著者和编译者做了较详细介绍。同时，对辞典内容进行了分类整理，并加以分析，认为《代数学辞典》一书适应了中学教育状况的需求，并对后来教科书的编排产生了积极影响。

新亚书店；代数学辞典；长泽龟之助；薛德炯；吴载耀

20世纪20年代末至30年代初，国民政府制订了“三民主义教育方针”，即“中华民国之教育，根据三民主义，务期民族独立，民权普遍，民生发展，以促进世界大同。” 这期间又相继颁布《中学暂行条例》、《中学法》和《中学规程》等一系列教育法令规程，旨在对中学教育制度进一步修改，以逐步形成一套完整的中学教育制度。中学新课程标准的实行，对新教材、新课本的选取和编排提出了新的要求。但是，此时我国自编教材面临着诸多困境，在这种背景下，我国学者翻译了大量的外国现行教材，有日本的，也有欧美的。这些汉译课本很好地解决了当时中学教材青黄不接的难题，对中国教育的发展产生了深远的影响。其中《题解中心算学辞典》中的《代数学辞典》原著者为日本数学家长泽龟之助，1935由我国学者薛德炯、吴载耀翻译完成并经上海新亚书店出版，1959年又由上海科学技术出版社重印出版，在我国产生了较大的影响。

1 《代数学辞典》编著者和中译本编译者

1.1 原书的编著者

19世纪末，日本进行了一场自上而下，具有资本主义性质的现代化改革运动，史称“明治维新”。这一时期在教育上，日本天皇要求日本向全世界学习自然科学，政府命令“和算废止，洋算专用”。于是举国上下大兴西学。全盘的学习西方数学，不仅派留学生到欧美等发达国家学习，还聘请大量西方专家学者到日本访问指导。如菊池大麓、高木贞治、藤泽利喜太郎留学归来后被委以重任，他们不仅带来西方先进的数学知识，也把西方的教育理论、教学思想带到了日本。同时日本的数学家大量翻译西方数学著作，编译制定新式教材等。这些都使得西学在日本得到迅速普及，科学技术得到空前发展，日本也一跃成为亚洲第一强国。

《代数学辞典》是由日本著名数学家和数学教育家长泽龟之助编著而成，是《题解中心算学辞典》丛书之一。该辞典在日本出版后作为中学教材使用，深得师生欢迎。著者长泽龟之助，万延元年（1860年）出生于一个藩士家庭。早年接触新式的西方教育，明治十一年（1878年）毕业于长崎师范学校，之后自己在京都开办私塾，同时自学西方数学知识。明治十三年（1880年）加入东京数学会社，并有多篇论文见于《东京数学会社杂志》。后不久协助数学家川北朝邻从事欧美数学著作的翻译与出版。明治十六年，长泽龟之助在陆军部门进行数学教科书的编审工作，后又在多所学校任职。1906年，长泽龟之助自己创办数学杂志，同时仍继续从事数学教学和翻译工作，直到1927年去世。长泽龟之助一生著述150多种，并与我国学者周达、崔朝庆、薛光锜交往密切，对日本的数学教育和中日交流做出了重要贡献[2]。

1.2 中译本《代数学辞典》的译者

甲午战争后，清政府逐渐认识到自身的落后及中日国力的差距。日本经过明治维新，迅速强大起来。日本的数学水平已经远超中国，此时中国派遣大批留学生到日本学习，如冯祖荀、陈建功等。同时国内也掀起了教育改革的浪潮，废除科举、兴办学堂，颁布新学制等。民国初年又出台多条教育法令，将学堂改为学校，男女生可同校学习，废弃出身奖励制度。五四运动后，喊出了“教育救国”的口号，颁布“壬戌学制”，推行教育独立运动，缩短小学期限，延长中学教育，取消大学预科，实行“六三三制”。随着共产党的建立，开展了一系列的平民化、大众化的工农民众教育运动。同时国内中小学和大学普遍采用日本现行教材，直接用日本课本进行授课。但国内毕竟精通日语者少，特别是中小学校的学生。这种情况下，大量日本教材通过翻译、编排、出版，在当时成为一时的风气。翻译者多为留日学生，他们在日本教材的引进工作中扮演了重要角色。

《代数学辞典》的译者是薛德炯和吴载耀。薛德炯字晓升，1887年生于江苏江阴市城区东横街，是我国近代著名的教育家、书法家和辞书编纂者。他自幼聪明好学，博览群书，颖悟过人。早年曾在江阴辅延高等小学堂跟随王希玉读书。毕业后得到清廷驻德意志公使的欣赏，遂赴德国柏林使馆任使馆录事，同时刻苦自学德文和科学知识。1908年，薛德炯东渡日本，在早稻田大学半工半读。之后回国在辅延学堂、礼延学堂、南菁中学等处任教，因学识渊博，被学生称为“百科全书”和“晓夫子”。薛德炯同时广泛接触同盟会组织和地方进步人士，积极开展民主革命。1933年调往上海纺织工业专科学校兼课，同年应陈邦桢之邀，任新亚书店编辑，后一直从事编辑翻译工作，著名的有《题解中心算学辞典》、《英汉化学辞典》等。后者的编纂更耗费了他大量心血，除了广泛搜集资料外，还要自学俄语，前后共达7年之久。欣慰的是，后者终于在他近古稀之年得以出版。由于身患重病，行动不便，再加上长期工作的劳累，于1966年去世[3]。吴载耀，江苏江阴人。关于生卒年月，未见书面记载。早年他出资与陈邦桢一起创立了新亚书店，同时也担任书店编辑，编辑出版了多种图书，最著名的是与薛德炯一起编译了长泽龟之助的《题解中心算学辞典》。1956年，新亚书店公私合营后，出任教育图片出版社编务室负责人。

1.3该书的出版者

《代数学辞典》一书最早由上海新亚书店于1935年6月出版。该书店1927年建立在上海山东路（今山东中路），不久又迁往尚仁里、河南路等地。书店的总经理是原中华书局的陈邦桢先生，由于各种原因陈邦桢辞去中华书局的经理职务，独自创立了新亚书店。《代数学辞典》的译者薛德炯和吴载耀是新亚书店的主要编辑，也是该书店的股份者[4]。

新亚书店以出版中小学教学挂图、字画字帖、自然科学类书籍为主，其出版宗旨是面向中小学教育和大众科学文化普及。抗战爆发后又先后在成都、重庆、昆明、汉口、长沙、贵阳、广州、香港等地设立分店。同时出版了大量书籍及教材，不仅提高了书店知名度，也对我国的教育产生了重大影响。1956年5月参加了当时的公私合营，即私人所有改为集体共同所有。随后并入教育图片出版社，即现在上海教育出版社的前身[5]。

《代数学辞典》初版后，受到欢迎。1957年，考虑到当时教育状况及大众的需求，《代数学辞典》由上海的科学技术出版社再版重印，1959年，发行了新的版本。1981年，《代数学辞典》又一次重印发行。

2 《代数学辞典》中译本概述

2.1 《代数学辞典》中译本概况

《代数学辞典》于1935年6月由薛德炯、吴载耀二位学者编译出版，原书在日本出版后，获得专家学者一致好评，深受读者喜爱。译者在序言中说：“……环顾同业现况，小说出品，车载斗量，科学书籍，寥若晨星，深感无以应国人之所需要，颇思有所贡献……”。可见，在当时科学类书籍的出版甚少，数学类书籍更是如此。这样在新教育制度出台实施的情况下，数学教科书的“贫乏”显然无法跟上教育的发展。正是于此，受“新亚书店以编译日本长泽氏所著算学辞典相嘱”，薛、吴二人耗时4年，在日文原书的基础上几经修订、增补而成。中译本较原书也作了一些变动调整。比如：原书以问题解法某某辞典命名，编译后更名为辞典式算学题库；原书新增之题列入补遗之部，编译后编入相应分类中；原书名词之部以假名顺序编排，编译后改为笔画顺序，以方便中国读者查找。

图1 新亚书店出版的《代数学辞典》

图2 上海科学技术出版社的《代数学辞典》

《代数学辞典》一书共计4 515题、951页。分为卷首公式、附录英汉名词对照表和解法之部、名词之部、代数学小史之部三门。本书内容大致分为整式、分数、方程式及应用、幂、指数、对数、根数、虚数、级数、消元法及恒等式、不等式、极大极小问题、比例、物理学的应用、排列组合和或然率。

2.2 新知识、新内容

解法之部是本书的重点，涵盖了全部的4 515题的解法技巧及提示，有的甚至一题多解，这对于培养学生思维的敏捷性和灵活性大有益处。这不仅是一部大的题典，而且书中穿插有新的数学定理和公式，有助于学习者增长见识拓宽知识面。比如书中第3 939题的欧拉氏证法，第196题求解多项式整除的商及余数的Horner氏分离系数法等等。

下面以第196题为例，以观其一斑。

196.求解x5－5x4＋9x3－16x＋13除以x2－3x＋2所得之商及剩余。

先将被除数之系数，书于第一列，符号仍旧。其左行书除数之系数，但须直书，符号第一项仍旧，以下当变（正负号改变）。被除数第一项之系数，与其左行第二项以下相乘所得之积，书于第二列第二项之下。于是将第二项相加，得和-2，即商数中第二项之系数（第一项商之系数，为第一项被除数之系数）。复以此系数，与左行之第二项以下相乘，所得之积，书于第三列第三项以下。于是将第三项相加，得和＋1，即商中第三项之系数。但所求之商究至何处为止?欲解决此问题，则吾人可知被除数之第一项，除以除数之第一项，得商x3，故商之第一项为x3。由此可知，所求之商，至第四项而止。

上述表述用现代数学语言可表示如下：

由此得商x－2x＋1，剩余－15x＋11。

这些题是当时一般教材所没有的，作为学习者可以丰富自己的数学知识，甚至可以直接拿来作为定理使用，这对融会贯通所学知识大有好处。

书中有些题较为艰深，甚至涉及到高等数学知识。对于学有余力的优秀学生而言很有帮助，为以后继续深造打下了良好基础。如37页的第227题、228题就是一些初等函数展开式的证明，这些题不仅具有挑战性，也增加了趣味性，即初等函数可以表示成无穷个代数式和的形式。小于0.000014。

这些题是连接初等数学与高等数学的桥梁，对于以后从事高等数学知识有很好的过渡作用。无穷级数的展开在大学里是较难的部分，但这里却用初等方法以证明，不仅对学生起到很好的练习，养成良好的运算习惯，也使其认识到高等数学并非想象的那么难，进而从根本上解决了学习数学的恐惧心理。同时也让学习者了解到数学由“初等”到“高等”的发展过程。

2.3 应用习题

数学者，学以致用。书中的数学知识在熟练演算后，都附有大量的应用题，即用数学手段解决实际问题。如用数学知识解决物理问题，不仅数学公式得以熟练，物理知识也得以融会贯通，起到了多重功效。同时通过这些应用题让我们认识到数学知识的普遍性、重要性和趣味性。书中专门分章节罗列应用题的有：一元一次方程式之应用、联立方程式之应用、一次分数方程式之应用、物理学的应用、比及比例的应用、一元二次方程式之应用、联立二次方程式之应用等多达数百页，此外一些章节中还穿插有实际应用题，如行船问题、追击问题、利息年金问题等。下面仅列3题以供说明。

2365.一农夫，有矩形牧场，广0.968亩，其周围以木板，共176块，每块长2尺，然则此牧场长阔每边用木板几块?

3181.常人之明视距离为12寸，某老眼者之明视距离为20寸，则其所用之眼镜，当为几度?

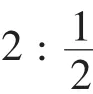
从这几个题中，我们可以看出，题的难度并不大，语言也通俗易懂。只要具备基本的知识，再加上分析处理问题的能力，这些应用题就迎刃而解。如2 365题，只要知晓矩形的面积周长公式，以及面积亩与平方尺的换算关系。然后设长边为x，阔边为y，联立二元一次方程即可解出。数学思维是靠锻炼的，编者之所以花大量篇幅收录应用题的原因也在于此。旨在培养学生从算术到代数的观念转化，由具体的形象思维到抽象的逻辑思维的过渡升华。

2.4 经典习题

仔细对比书中习题和现在习题的区别，可以发现很多题型差别并不大，书中题型之广是市面一般参考书难以觅到的。甚至现在一些收编的习题都是抄录自《代数学辞典》，可以说书中习题很典型。更有一部分可以称之为经典的习题，比如丢番图年龄之谜、时针问题等。

873.或问时刻，答曰：今在Ⅹ时与Ⅺ时之间，6分后之分针，与3分前之时针，适相反对，然则今为何时?

之所以说是经典习题，主要是因为时间渊源较长，且题型极具代表性。学生做过这些习题后，可以起到触类旁通，事半功倍的效果。比如第848题将丢番图的一生划分为6个阶段，每个阶段既有整数表示也有分数表示。这将迫使学生思考设什么为未知数，如何列方程等。这些对学生的数学思维是一个很好的锻炼过程。

2.5 数学史部分

书中专门设有代数学小史之部，共计36页。从公元前1 600年的阿梅斯 （Ahmes）到19世纪的德·摩根 （Augustus De Morgan）共63位数学家的小传。对每个人的生平事迹、数学贡献和文章著作都有所介绍。文中还重点介绍了符号代数学的发端，代数学上通用符号（加减乘除号、等号、不等号、幂号）的起源。对部分数学家的工作进行了详细解读，比如韦达、帕斯卡、高斯、柯西等。这些知识有助于学习者厘清数学定理的发展脉络，激发进一步学习的兴趣和热情。文中出现的很多数学家著作、事迹，即使对专业数学史工作者而言，也有重要的参考价值。如938页对数学家费马的介绍：

氏最喜研究整数论、Diophantus氏书，氏拟刊行，故随在附有注释，其中富有至理，皆载入遗著第二卷。氏之证明散佚者多，兹就流传之定理中举其最著名者如下：

（a）设p为质数而a对于p亦为质数，则ap－1－1得为p所整除。即

ap－1－1≡0（modp）

此定理Euler氏始证明之。其普遍之形式应为

a覬（n）－1≡（mod n）

a对于n为质数，覬（n）为小于n之整数之个数而对于n为质数者。

（c）三个整数之平方和不能等于两个平方数之和。此定理出于Diophantus，而氏附以系曰，质数之成（4n－1）形者，其质倍数（即乘以对于本数为质数之数所得之积）不能为平方数；且不能为两个整数或分数之平方和。

例如，11得化成（4×3－1）形，而4对于11为质数，故4×11即44不能为两个平方数之和。

（i）n为大于2之整数时，方程式xn＋yn＝zn无整数解答。

本定理以其普遍的论证，尚未经人举出，故极有名。Euler氏在其著作《代数指南》中以n＝3为例以证之；Lagrange氏在1 777年就n＝4之例以证之。Kummer氏曾用Ideal primes证明本定理除小数之特别情形外余皆合理；惟其证法繁杂，盖与氏所发现者不同。故本定理虽应普遍合理而迄今仍有待于能解之者。

以上3个是费马最具代表性的数学成果，分别是费马小定理、平方数和费马大定理。这些数论问题推动了整个数学的发展，特别是费马大定理，这只“会下金蛋的鸡”催生出了许多著名的数学成果。如代数数论、解析数论等。文中还详细介绍到欧拉、拉格朗日、库默尔等人的工作，这对于数学史家研究费马大定理的证明历程以及数学思想的发展都有很重要的作用。另外这些无疑扩展了学生眼界，培养了其学习数学的兴趣和热情。

3 《代数学辞典》的影响

《代数学辞典》一书由新亚书店、科学技术出版社和上海科学技术出版社先后出版。由新亚书店出版的时间从1935年6月至1953年3月，共计9版，23500册；科学技术出版社从1957年9月至1958年2月，共一版4次印刷，印数30 000册；上海科学技术出版社从1959年10月新一版印刷，至1981年1月，共印刷3次，印数达到177 000册。《代数学辞典》在近半个世纪的时间中先后被三大出版社出版和重印，总印数达到230 500册，其产生的影响是不言而喻的。

据相关资料显示[6]，新亚书店在抗战时期内先后在全国各地设立了十几家分店，这对书籍的销量及产生的影响无疑是巨大的。据统计当时书店月平均销售《代数学辞典》达到155部。薛德炯先生于1957年在该书重版赘言中写道：“……那知两年以来，存书早已卖尽，不见于市，上海旧书店且在高价收买，而来源缺缺。各地读者纷纷向新华书店采购，无以供应。”足见当时该书销量之火爆，甚至高价钱都很难买到。

《代数学辞典》一书可以说影响了几代人，甚至很多年后的今天对他们还有很深的印象。著名学者林公武在访谈中说道：“所以当我在四十多年后再翻阅这本《代数学辞典》时，可以说对于我们这些身为‘老三届’的学生，‘无法抚慰的岁月’怎能忘怀……”[7]。北京航空航天大学原校长、中国科学院院士李未在辽宁省实验中学的60周年庆典中说道：“我读遍了图书馆所藏的代数和几何参考书，把书上的习题全做完了。到最后，图书馆老师搬出了馆藏的长泽龟之助的《代数学辞典》来给我看……”[8]。甚至文学家鲁迅先生当年从日本回国时，也带回了长泽的《代数学辞典》，后赠于青年学生王铎中，该书现陈列在绍兴鲁迅纪念馆。

虽然《代数学辞典》发行至今已经近80个年头，但书中的习题对当今数学教育仍然具有重要意义，正如有的学者所言：“为了让教师积累大量的典型数学题，我们要求教师深入学习经典。如上海科学技术出版社的日本的长泽龟之助原著薛德炯、吴载耀编译的《题解中心算学辞典》”[9]。

一本书的出版至今已越过了半个多世纪，却仍然受欢迎受重视。书中的很多习题更是见诸于各大中学课本，甚至书本身的编排特点也被今人所研究，这在现代数学史上是不多见的。

[1]魏庚人.中国中学数学教育史[M].北京：人民教育出版社，1987：226.

[2]冯立昇.中日数学关系史[M].济南：山东教育出版社，2009：280-282.

[3]江阴县文史资料研究编委会.江阴文史资料（5）[M].1984：87-91.

[4]赵永良.无锡名人辞典[M].南京：南京大学出版社，1989：164.

[5]宋原放，孙颙.上海出版志[M].上海：上海社会科学出版社，2000.

[6]余嘉.建国初上海的书店出版社情况摘编[J].上海：上海书店出版社，1991（1）：121.

[7]摇摇.墨兵千万尽驱使[J].海峡通讯，2007（2）：61.

[8]李未.在辽宁省实验中学建校60周年报告会上的讲话［DB/0L］.辽宁省实验中学网站，2009-05-14.

[9]顾荣.“磨题”：走向共生的数学教师校本研修方式[J].江苏教育研究，2007（12）：21.

〔责任编辑 李海〕

Introduction to Chinese V ersion of“Algebra Dictionary”

YAN Xiao-min
（Institute of History of Science and Technology，Inner Mongolia Normal University，Hohhot Inner Mongolia 010022）

The translation of"The algebra dictionary"in our countrymakes a significant influence.The paper analyzes the publishing background between Japan and China，and does amore detailed introduction for the original author and translators.After sorting and analyzing of the Dictionary，the author geta conclusion the dictionary adapt to the needs of the situation of secondary education，and had a positive impacton the scheduling of the later textbooks.

Xinya Bookstore；Algebra Dictionary；Kamenosuke Nagasawa；Xue Dejiong；Wu Zaiyao

N09

A

1674－0874（2012）02－0092－05

2011－09－12

闫晓民（1983－），男，河北邯郸人，硕士，研究方向：数学史。