光子石墨烯中光传输特性的研究
2012-09-12刘艳红石云龙
刘艳红,石云龙
(山西大同大学物理与电子科学学院,山西大同0370009)
光子石墨烯中光传输特性的研究
刘艳红,石云龙
(山西大同大学物理与电子科学学院,山西大同0370009)
光子石墨烯与电子石墨烯有相同的微结构,是具有三角晶格的二维光子晶体,其能带结构中存在中心奇异点,称为狄拉克点。这种狄拉克准粒子的存在导致了一种新的传输状态“赝扩散”。利用共面接地波导实现了单方向性窄的波束通过二维光子晶体。利用数值仿真的方法验证了“赝扩散”的传输特性。实验结果表明,对于二维光子晶体有些能带是不能被激发的。
光子石墨烯;接地共面波导;狄拉克点;赝扩散
自从2004年K.S.Novoselov[1]等人成功地从石墨剥离得到单原子层石墨晶体后,石墨烯以其优异的力学、电学性能和巨大的应用前景成为当今自然科学领域研究的热点[2,3]。石墨烯不同寻常的性质来源于它完美的二维晶体结构和奇妙的电子态性质。石墨烯是由碳原子周期排列成蜜蜂窝形状而构成,具有六边形对称性。在固体物理中,薛定谔方程可以描述几乎所有材料的电子特性。但是石墨烯是一个例外,其电子性质用量子力学的狄拉克方程来描述[4]。计算石墨烯的能带结构会发现在三角晶格布里渊区的边界点上形成了上下锥形的形状,在布里渊区的顶角上,其电子特性具有线性色散关系,锥形的中心叫做狄拉克点。这与一般材料如普通的正方晶格材料的能带结构完全不同,后者的能带成抛物面形。正是石墨烯中这种独特的电子特性,使石墨烯表现出了很多奇特的物理性质如颤动和“赝扩散”效应等[5-7]。
本文我们研究一种光子晶体结构,它的光学性质类似于石墨烯的电子能带结构,展现出线性的能动量色散关系。电子在石墨烯中奇特的物理性质激发了人们研究光子在类石墨烯晶体中的传输特性。和石墨烯中的电子相比,在类石墨烯光子晶体中的光子的麦克斯韦方程可以演化为狄拉克方程。在二维三角晶格光子晶体里,可以得到相同的锥形能带结构[8,9]。这样可想而知,光子在类石墨烯光子晶体中一定会有奇特的传输特性。而且光子比电子有优越性,光子是电中性的无质量的玻色子,不会受到库仑力和质量密度的扰动。所以更容易去研究证明二维是石墨烯晶体的一些奇特物理性质。光子在类石墨烯光子晶体中传播时,其色散关系也满足线性色散,可以找到狄拉克点对应的频率。这个频率的光子在晶体中传播时满足“赝扩散”行为。即透射系数会随着传播长度变化,而且在狄拉克点出会出现极值。这与光子在晶体中的其他传播方式有很大不同,处于通带的光子其透射系数不随传播长度变化,而处于禁带的光子是完全不透射的。狄拉克点处的光子的传播方式介于这两者之间透射系数随着传播长度增加而减小,这就是所谓的“赝扩散”行为。
最近关于微波光子晶体中的狄拉克点附近奇特传输性已经有实验研究[10-13]。2010年,S.R.Zandbergen等人已经在实验中观察到了在类石墨烯光子晶体中的赝扩散传播行为。同年,A.Richter等人也通过微波实验观察了狄拉克点的存在。在以上的微波实验中作者用到的都是喇叭天线发射和接受信号,而从喇叭天线出来的信号不容易有好的单向性穿过光子晶体所以测量效果不好,较多的信号被发散了。在我们的工作中,以接地共面波导为研究平台,这样就可以提供很好的单向性,更有利于研究二维光子晶体的传输特性。共面波导包含有4个平行的电极,中心电极是信号电极,其它3个电极是接地板,中间层是介质层。图1中给出了接地共面波导的原理图及电场分布图。

图1 (a)共面波导的结构示意图,(b)场分布图
在许多方面用二维光子晶体板来研究二维光子晶体的性能。在图2中给出了二维光子晶体板的结构示意图。

图2 二维光子晶体板的结构图
在本文中我们考虑三维的类石墨烯光子晶体板,其结构是在高介电介质板上钻空气孔,介电常数为a,孔的半径为R及介质板的相对介电常数εr分别为0.35 a和10.2。光子在类石墨烯光子晶体的传播可以由式1表示。

式中,Ψ=(Ψ1,Ψ2)表示在狄拉克点处两个布洛赫波的振幅,狄拉克点处的频率ω和速度vD的大小与光子晶体的结构参数有关。对于一个宽的而且短的二维光子晶体(W〉〉L),可以利用光子晶体板的周期性边界条件得到微波传播的特性T∝1/L,T为透射系数。
1 狄拉克点的计算
电磁波在二维光子晶体中的传播已经有很多理论和实验研究。许多作者利用平面波展开的方法理论,计算了二维光子晶体的色散关系曲线[14-16]。一个直截了当的计算光子能带结构的方法是有限时域差分法[17]。本文我们利用三维时域有限差分法计算了光子晶体的能带结构见图3。能带结构中最显著的特点就是在布里渊区的边角处找到狄拉克点,对应频率分别是f=0.238 c/a和f=0.505 c/a,其中c是真空中的波速。
2 数值仿真及结果分析

图3 (a)横电波模式的三角晶格的能带结构图(b)光子晶体的第一布里渊区
本文中用到的接地共面波导的特征阻抗Z0是50Ω,中间电极的宽度是40 mm。数值仿真软件是基于有限元法的CST商业微波仿真软件。仿真过程用到的光子晶体板的参数是共有27行半径为0.35 mm的空气孔,晶格常数是a=20 mm板子的高度是h=1,5 mm。为了观察在狄拉克点处的具有极值的透射谱及赝扩散现象,我们设置了不同长度的二维光子晶体144 mm~344 mm。
图4中,给出了不同长度的二维光子晶体的透射谱。从图4中可以看到在狄拉克点f=0.505 c/a对应频率为7.5 GHz处透射谱处于极值点,而且随着长度的增加透射系数满足T∝1/L。
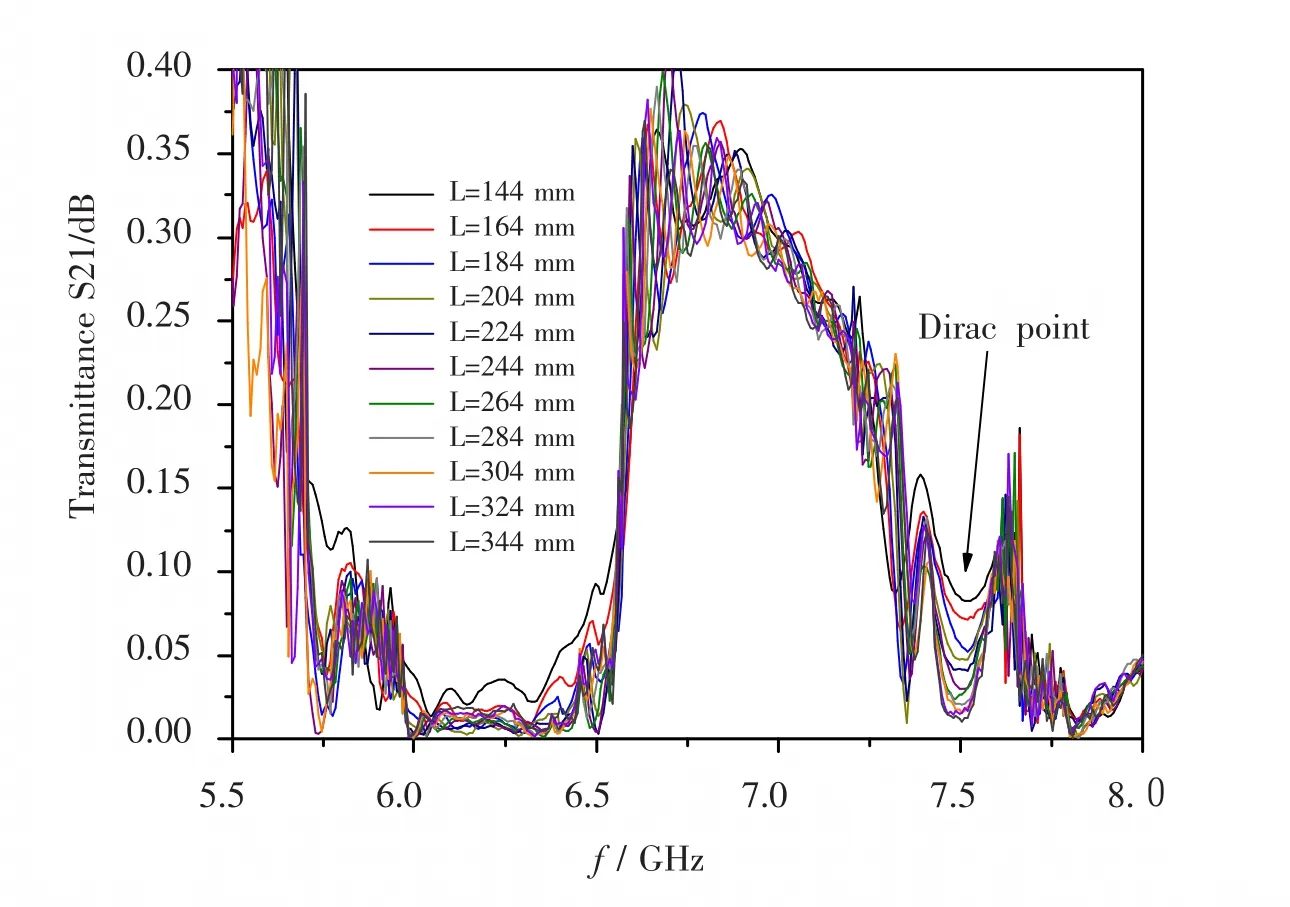
图4 同一光体晶体结构不同长度的透射谱
3 讨论及实验验证
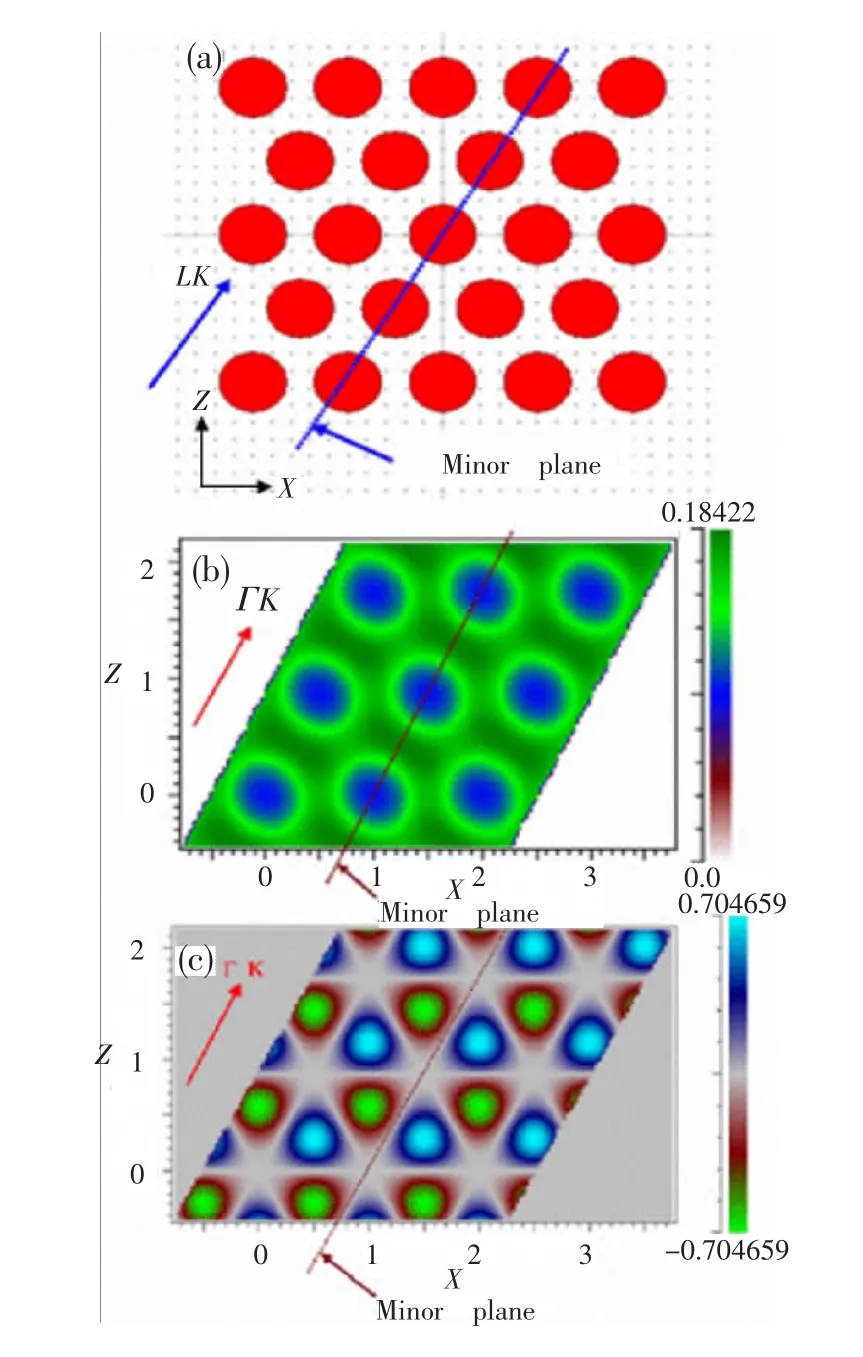
图5 (a)场模式的数值仿真结构
下面我们来解释为什么在狄拉克点的理论计算中有两个狄拉克点频率,而在实际的数值仿真结果中却只能找到高频的狄拉克点。为什么低频的狄拉克点会消失?在文献[18]中,作者提出根据能带的场的模式可以判断出有些平面波波前不能激发某些模式。本文中我们计算了沿着ΓK方向入射时的能带结构它是布里渊区中的一个特殊的方向。在物理机制中这就意味着沿特殊方向入射的平面波必须要么是奇对称模要么是偶对称模对应于反射镜面。在图5中给出了电场分布图。从图5(c)中可以看到对于能带2的场的模式是关于反射镜面是奇对称的。然而入射平面波当电场方向沿着柱子的轴向时场的模式应该是偶对称的,所以说第二个能带是不能被激发的。在图5(b)中可以看到对于能带一场的模式是偶对称的是能够被激发的更证明了我们的分析是正确的。
本文实验研究了长度为144mm的类石墨烯光子晶体的板的光传输谱。微波是由安捷伦公司的网络分析仪(Agilent8722ES)产生然后连接到共面波导上最后再输出到网络分析仪上,就可以测量到透射谱。图6中给出了电磁波沿着ΓK方向的透射系数。由图6中的阴影部分我们可以看到第一个带隙的位置应该在相对应的频率为4.6 GHz-5 GHz,但是在仿真结果中我们看到的第一条带隙的频率范围是3.6 GHz-5 GHz。也就是说,第二条能带没有被激发出来。从实验结果可以看到在频率范围3.6 GHz-5 GHz有明显的带隙存在。关于带隙的带边实验与仿真吻合的很好,但是带隙的深度存在一些差异,原因是我们实验中用到的高介电介质板存在色散,随着频率的增高色散也越严重所以会有差异。即使这样我们依然可以证明第二条能带是不能被激发的。
4 结论
我们利用接地共面波导为仿真实验研究平台代替前期的喇叭天线实现了好的方向性的窄的波束这样有利于研究二维光子晶体的性质。从数值仿真的结果可以看到,对于类石墨烯光子晶体,当光子的频率达到狄拉克点频率时其透射谱会有极值出现,而且随着光子晶体长度的增加,透射系数会递减,很好得验证了光子在类石墨烯光子晶体中的“赝扩散”行为。另外我们进一步实验验证了对于二维光子晶体,当平面波以特殊方向入射时场的模式是唯一的所以有些能带是不能被激发的,实验结果和理论结果符合的很好。
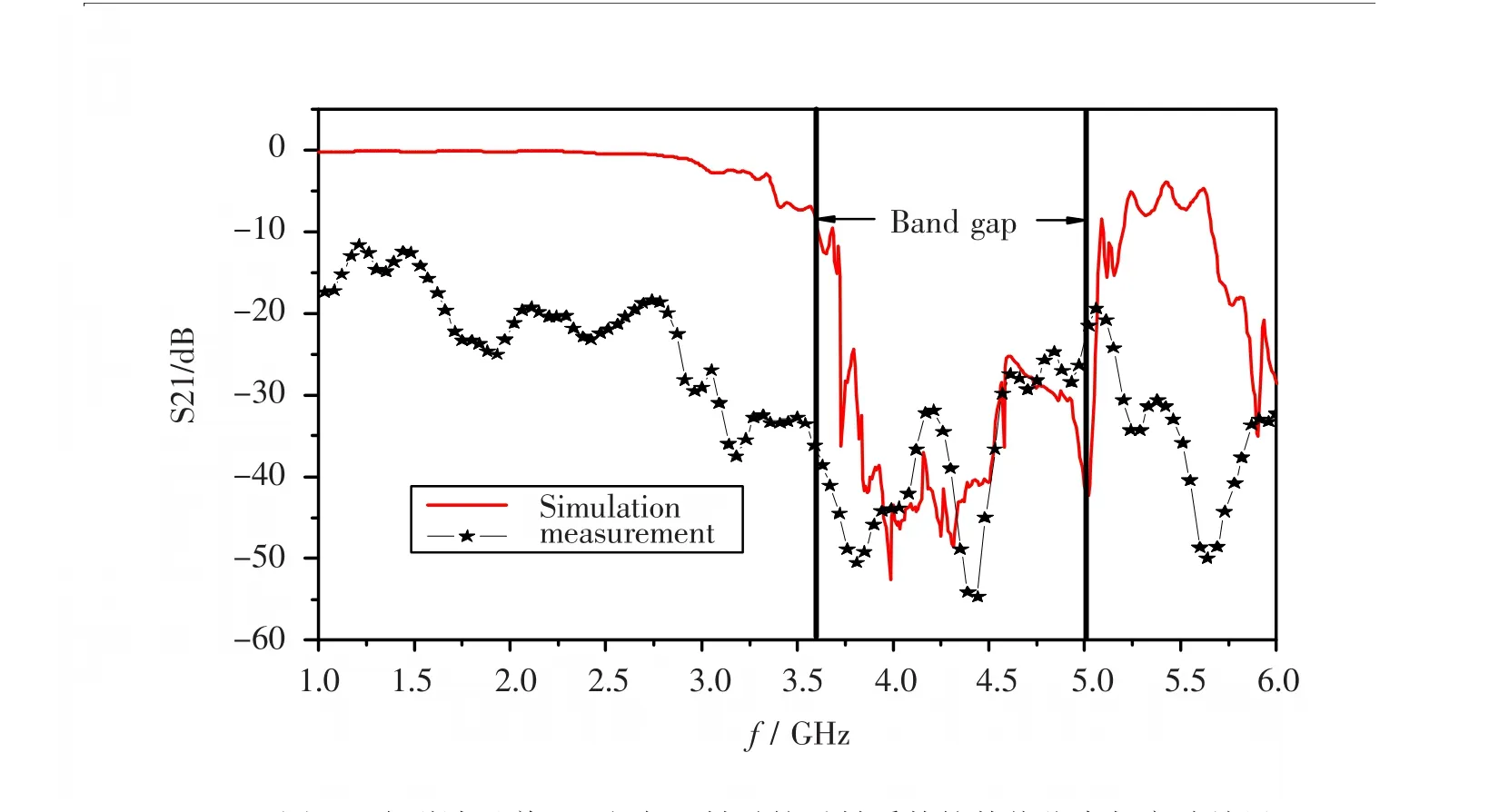
图6 电磁波沿着ΓK方向入射时的透射系数的数值仿真与实验结果
[1]Novoselov KS,Geim AK,Morozov SV,etal.Electric field effectin atomically thin carbon films[J].Science,2004,306:666-669.
[2]Castro Neto A H,Guinea F,Peres NM R,etal.The electronic properties ofgrapheme[J].Rev Mod Phys,2009,81:109-162.
[3]Beenakker CW.Colloquium:Andreev reflection and Klein tunneling in grapheme[J].Rev Mod Phys,2008,80:1337.
[4]Geim A K,Novoselov K S.The rise of grapheme[J].Nature Materials,2007,6:183-191.
[5]Wallace PR.The Band Theory of Graphite[J].Phys Rev,1947,71:622-634.
[6]Ando T.Theory of electronic states and transport in carbon nanotubes[J].JPhys Soc Jpn,2005,74:777-817.
[7]Katsnelson M I.Zitterbewegung,chirality,and minimal conductivity in grapheme[J].Eur Phys J B,2006,51:157-160.
[8]Sepkhanov R A,Bazaliy Ya B,Beenakker CW J.Extremal transmission at the Dirac pointof a photonic band structure[J].Phys Rev A,2007,75:063813.
[9]Raghu S,Haldane F D M.Analogsofquantum-Hall-e ffectedge states in photonic crystals[J].PhysRev A,2008,78:033834.
[10]Zhang X D.Demonstration ofa new transport regime of photon in two-dimensional photonic crystal[J].Phys Lett A,2008,372:3512-3516.
[11]Zandbergen SR,de Dood M JA.Experimental observation of strong edge effects on the pseudodiffusive transport of light in photonic grapheme[J].Phys Rev Lett,2010,104:043903.
[12]Deligeorgis G,Dragoman M,Neculoiu D,etal.Microwave propagation in graphem e[J].Appl Phys Lett,2009,95:073107.
[13]Bittner S,Dietz B,Miski-Oglu M,et al.Observation of a Dirac point in microwave experiments with a photonic crystal modeling grapheme[J].Phys Rev B,2010,82:014301.
[14]Robertson W M,Arjavalingam G.Measurement of the photonic crystal in a two-dimensional periodic dielectric array[J].Phy Rev Lett,1992,68:2023.
[15]PlihalM,Shambrook A,Maradudin A A,etal.two-dimensionalsystems:The triangular lattice[J].Opt Commun,1991,80:199.
[16]Meade R D,Rappe A M,Brommer K D,et al.Photonic band structure of Accurate theoretical analysis of photonic band-gap materials[J].Phys Rev B,1993,48:8434.
[17]Taflove,Allen.Computational electrodynamics:The finite-difference time-domainmethod[M].Boston:Artech House,1995.
[18]Robertson W M,Arjavalingam G.Measurementof photonic band structure in a two-dimensional periodic dielectric array[J].Phy Rev Lett,1992,68:2023.
Investigation of T ransm ission P roperties in the P hotonic G rapheme S lab
LIU Yan-hong,SHIYun-long
(School of Physics and Electronics Science,ShanxiDatong University,Datong Shanxi,037009)
In this letter,we investigate the properties of the photonic grapheme which has the similar microstructure with the electric grapheme.In photonic graphene,there exist the Dirac points in the energy bands on hexagonal conrners of the honeycomb lattice Brillouin zone.The presence of Dirac point leads to a new"pseudo-diffusive"transport regime.We realize the narrow electromagnetic beam by using grounded coplanar waveguide with better direction.The extremal transmission of themicrowave near the Dirac pointhas been demonstrated bymeans of the numerical simulation.Furthermore,we verify experimentally that some certain electromagnetic field modes for photonic bands cannotbe excited in the photonic crystal slab.
photonic grapheme;grounded coplanarwaveguide;Dirac point;pseudo-diffusive〔责任编辑 李海〕
O571.5
A
1674-0874(2012)02-0014-04
2012-01-15
山西省高校科技研究开发项目[20111119]
刘艳红(1979-),女,山西文水人,博士,讲师,研究方向:凝聚态物理。
