应用连续墨西哥帽小波变换对弱信号提取分析研究
2012-09-12薛泽春李永刚李连之张宪玺
薛泽春,李永刚,李连之,张宪玺,刘 颖
(1.山东省化学储能与新型电池技术重点实验室,山东 聊城 252059;2.聊城大学化学化工学院,山东 聊城 252059)
在进行色谱分析或光谱分析过程中,信号强度较弱或噪声信号较强,会造成信噪比较小,使有用信号不能完全充分反映试样的信息,或分析样品含量很低,信号较弱,而应用小波变换,可发现合适信号[1].目前,小波分析在故障诊断、图像处理、语音识别、光谱分析[2]等领域得到了广泛应用.在光谱分析中,由于小波分析具有优良的多分辨率分析特性[3],利用小波多尺度分析可把信号分解成高频和低频成分,实现去噪功能[4].
小波变换主要是基于小波时频局域化特性,频率成分在时间轴上位置保持不变,频率变换不影响信号的线性[2,5-6],能够同时展现信号时间-频率性质.在获取试样信号过程中,噪声信号一般频率较高,而有用信号频率较低,小波变换可以将信号按频率分开.
1 小波变换原理

a用于控制伸缩,称为尺度参数,b用于控制平移位置,称为平移参数,φa,b(t)称为小波函数.小波变换为某信号f(t)∈R在小波域的投影,通常定义为f(t)和φa,b(t)的内积,即:
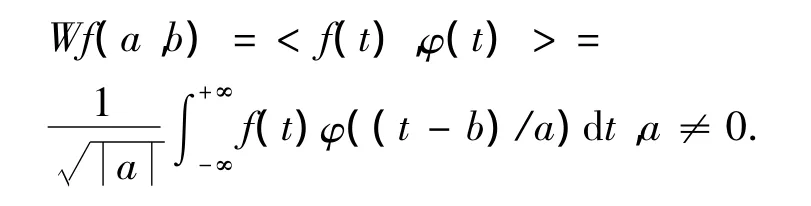
小波变换由于a,b可变且具有时频局部化特征,因此对非平稳信号显示出了独特的分析能力.在小波分析中,随着尺度因子a的增大,小波φa,b(t)的窗口逐渐加宽,在时间轴上考虑范围大,而在频域上相当于用低频小波作概貌分析,对于较高频率的噪声信号滤波能力也随之增强[10].在低频时,小波变换的时间分辨率较差,而频率分辨率较高;在高频时,小波变换的时间分辨率较高,而频率分辨率较低.所以小波变换被誉为“数学显微镜”[11-12].
小波基的选取应从一般原则和具体对象两方面进行考虑.一般原则包括正交性,紧支集,对称性,平滑性.要完全满足以上特性是十分困难的,小波的选取也没有形成统一的标准[13].可以采用尝试的方法从多个小波基中选取合适的小波.
连续小波变换可以在较大的伸缩尺度上观察信号的变化趋势,变换系数用小波函数与信号相似性程度表示.系数大说明信号与小波函数相似程度大,选择小波系数可以重现原信号.在低尺度下,含有较多的噪声信号,而在大尺度下基本上是要研究的信号,因此对小波系数累积求和,就可放大原信号.
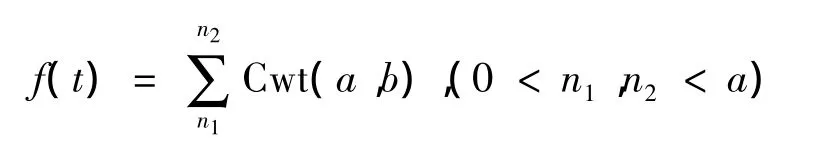
通过小波系数求和,就可以将噪声中难以识别的信号强化,从而发现被原始信号掩盖的信号.
2 实验过程
2.1 模拟信号
分析信号多为高斯峰,应用Matlab模拟一信号,并且为噪声信号所淹没,不能有效进行定量定性分析.
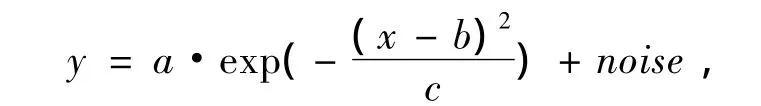
取a=2,b=200,c=40,noise为噪声,信号谱图如图1所示.信号被噪声完全覆盖,不能有效区别有效信号,也不能进行定性、定量分析.

图1 模拟信号
2.2 对信号进行连续小波变换
用 mexh,db4,coif4,haar,meyr,morl小波分别对图1信号进行连续小波变换,并将变换系数求和,将弱信号放大,寻找最佳小波形式.
3 结果与讨论
3.1 合适小波函数的选择
用 mexh,db4,coif4,haar,meyr,morl小波对图1信号进行连续小波变换,并将变换系数求和,放大信号如图2所示.
从图2 可以看出,a,b,c,f在时间为 200 处出现强峰,此处正好是模拟信号的峰位置,因此mexh,db4,coif4,morl能够反映出信号位置,但是b,c,f杂峰比较多,不如 a平滑;d,e在时间为200处没有出现信号峰,不能反映模拟信号的位置.综上所述,最好选择墨西哥帽小波进行小波变换.
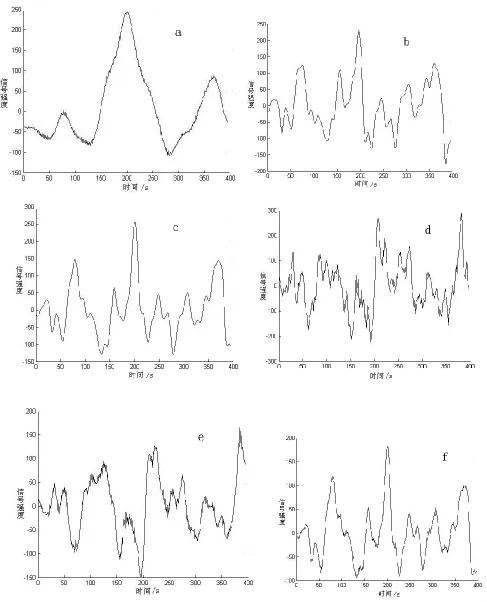
图2 连续小波变换后小波系数求和(a ~ f小波函数分别为 mexh,db4,coif4,haar,meyr,morl)
3.2 连续小波变换找出有效信号
将模拟信号用墨西哥帽小波进行小波变换,尺度a取值为1∶96.如图3所示,在低尺度,也就是频率较高的信号,是噪声信号的小波变换系数;在大尺度,是频率较低的信号,是有效信号的小波变换系数.所以通过小波变换可以将混合信号按频率分开.

图3 模拟信号连续墨西哥帽小波变换图
在图3中,颜色的深浅代表小波系数的大小,颜色越深小波系数越大.从图3可以看出,信号在时间为200的点处,各尺度的小波系数最大,此处也正好是信号的位置,说明通过小波变换可以找到信号峰的位置.
3.3 弱信号的放大
除去高频的噪声信号将小波变换系数加和,就可以将原来的弱信号放大,而峰位值不变.图4为不同尺度条件下求和后作图.
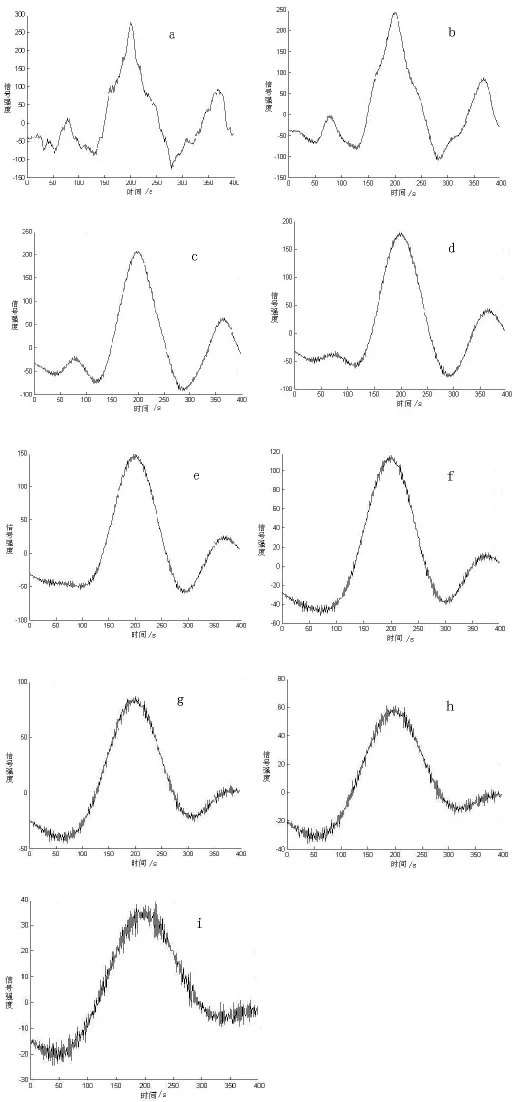
图4 模拟信号连续墨西哥帽小波变换系数求和a~i分别为1~96、10~96、20~96、30~96、40~96、50~96、60~96、70~96、80~96小波系数之和)
从图4可以看出,利用小波变换后系数求和可以放大原信号,但是求和范围不同,所得图形不一样.范围较小时,信号平滑性较差,不符合高斯线性关系;范围较大时,信号夹杂很多噪声信号,原因是连续小波变换会造成冗余信号.因此,通过观察最好从c、d、e中选择,这里我们选择d来进行定量计算.
3.4 信号定量分析
将模拟信号按比例增大,然后用连续墨西哥帽小波变换,求其变换系数,加和以放大信号,研究其线性关系.

a=2,a=3,a=4,a=6,b=200,c=40分别作图如图5所示.
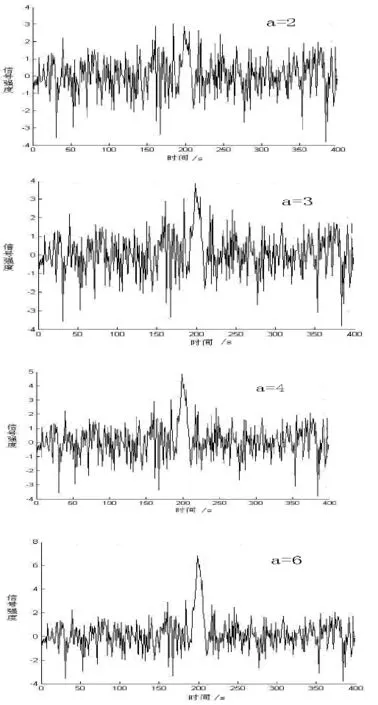
图5 a=2,a=3,a=4,a=6 时模拟信号
在图5中,有效信号被噪声信号覆盖,难于定量分析,将其用连续墨西哥帽小波变换,求其30~96层小波变换系数之和,并对时间作图,如图6所示.

图6 模拟信号小波系数之和与时间关系图
在原始模拟信号中不能观察到的信号通过小波变换被放大,峰位值不变,并且能够进行定性定量分析.
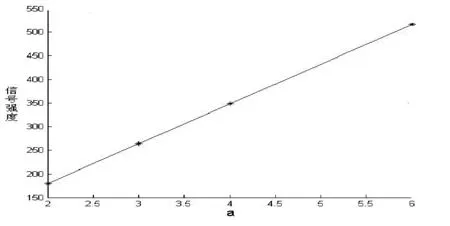
图7 信号强度与a值线性关系曲线
4 结语
弱信号分析是分析化学的一个重要方向.将信号通过连续墨西哥帽小波变换,频率高的噪声信号在尺度因子较小的位置,频率较低的信号在尺度因子较大的位置.通过连续墨西哥帽小波变换能同时展现信号的时-频信息的特点,从而能够找出有用信号,将埋藏在噪声信号中的有用信号小波变换系数加和,可以将弱信号放大,信号强度不同,小波变换系数加和也不同,并且具有良好的线性关系,能够作为定性定量分析的依据.
[1]卢礼萍,朱旭东,魏良淑,等.不同辐照下大豆胰蛋白酶抑制剂荧光的小波分析[J].甘肃农业大学学报,2011,46(2):147 -151.
[2]朱殿明,金万祥,骆晓森,等.人血清卟啉荧光光谱的双正交样条小波识别[J].光谱学与光谱分析,2008,28(8):1879-1881.
[3]顾振普,郑广.心电信号小波分析[J].河北科技大学学报,2006,27(4):328-331.
[4]周丹,王钦军,田庆久,等.小波分析及其在高光谱噪声去除中的应用[J].光谱学与光谱分析,2009,29(7):1941-1945.
[5]宋宁,周新勇,徐晓轩,等.基于小波变换的藻类显微光谱成像分类技术[J].发光学报,2007,28(6):954-958.
[6]王书涛,王玉田,车仁生,等.基于小波变换的叶绿素荧光光谱测量系统研究[J].应用光学,2005,26(1):49- 52.
[7]倪雪春,杨慧中.基于小波变换测定水质中硝酸盐含量[J].光谱实验室,2009,26(5):1175 -1178.
[8]张悦,杜守军,张丽梅.小波奇异性在钢结构损伤检测中的应用[J].河北科技大学学报,2010,31(2):151-157.
[9]郁青春,张世超,王新东,等.小波变换方法消除热重实验噪音信号[J].北京科技大学学报,2007,29(5):532-536.
[10]陈昌国,龙英,李纳.化学信号小波变换的本质分析[J].渝西学院学报:自然科学版,2003,12(14):5-8.
[11]杨福生.小波变换的工程分析与应用[M].北京:科学出版社,1999:89-90.
[12]马丽萍,石炎福,余华瑞.小波分析及其在化工信号分析处理中的应用及展望[J].化工进展,2005,24(2):147-153.
[13]刘素美,李书光.超声检测信号处理的小波基选取[J].无损探伤,2004,28(6):12 -15.
