三维空间中Navier-Stokes 方程的有限差分方法
2012-09-12杨雪敏郑治波狄华斐
杨雪敏,郑治波,狄华斐
(1.云南师范大学数学学院,云南 昆明 650092;2.云南民族大学数学学院,云南 昆明 650500)
研究三维Navier-Stokes具有非常重要的意义,但我们很难求得此方程的精确解.目前就理论上做了少量工作,构造了部分精确解.理论上进展缓慢,主要是人们不知道从何处入手.然而,数值解将会提供一些信息.本文研究如下形式的三维 Navier- Stokes 方程[1-2]:

其中,F=F(u,v,w,t).u=u(x,y,z,t),v=v(x,y,z,t),w=w(x,y,z,t)分别表示流体的速度,p(x,y,z,t)是压强.方程(1)可以被写成:

1 三维Navier-Stokes方程向前差分格式的解与精确解的误差
1.1 讨论三维Navier-Stokes方程向前差分格式
首先,我们建立(2)式的向前差分格式,在建立之前,设

M是一个给定的正整数,对于三维空间区域作网格剖分,取空间方向步长为,时间方向步长为τ,而且分别记:

于是三维Navier-Stokes方程向前差分格式:

我们把(3)式进行化简整理得到:

1.2 画图误差
我们找到方程的一个精确解:
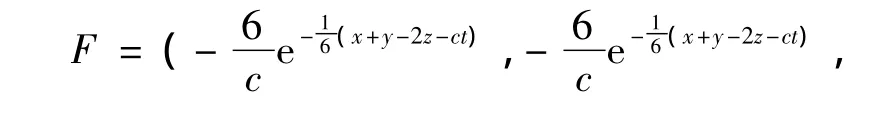

用我们编写的MATLAB程序求解,得出如下图:
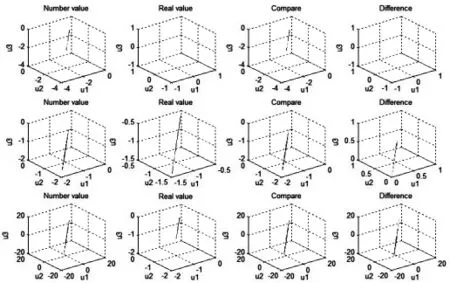
图1 t=1~3时(从行看)相应的差分的解的图真值图,两者的比较图,两者之间的误差图
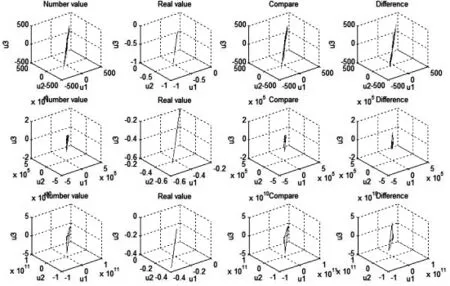
图2 t=4~6时(从行看)相应的差分的解的图真值图,两者的比较图,两者之间的误差图

图3 t=7~9时(从行看)相应的差分的解的图真值图,两者的比较图,两者之间的误差图
1.3 误差分析
图1~3分别为t=1~9(从行看)时,相应的差分的解的图,真值图,两者的比较图,两者之间的误差图.可以发现,当t=1~3时,吻合程度较好;随着时间的推移,吻合程度越来越差,变化程度越来越剧烈.
2 三维Navier-Stokes方程向后差分格式的解与精确解的误差
2.1 讨论三维Navier-Stokes方程向后差分格式
和前面的相同,我们构造了三维Navier-Stokes方程向后差分格式:

我们把(4)中的3个等式进行化简得到:

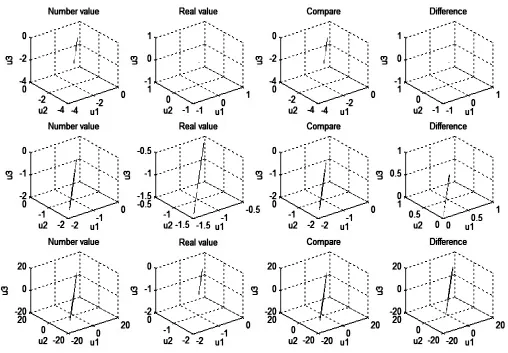
图4 t=1~3时(从行看)相应的差分的解的图真值图,两者的比较图,两者之间的误差图

图5 t=4~6时(从行看)相应的差分的解的图真值图,两者的比较图,两者之间的误差图
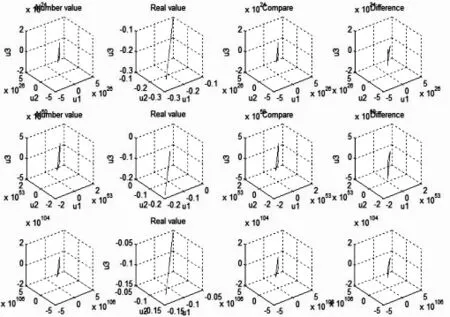
图6 t=7~9时(从行看)相应的差分的解的图真值图,两者的比较图,两者之间的误差图
2.2 画图误差
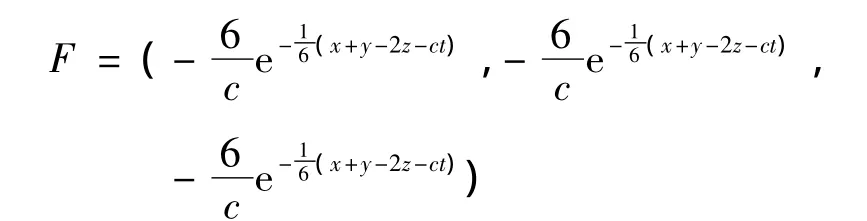
同样我们采用精确解作为方程的初值.用我们自己编写的MATLAB程序得到图4~图6.
2.3 误差分析
图4~图6分别为t=1~9(从行看)时,相应的差分格的解的图,真值图,两者的比较图,两者之间的误差图.可以发现,当t=1~3时,吻合程度较好.随着时间的推移,吻合程度越来越差,变化程度越来越剧烈.
3 结论
可以发现,当t=1~3时,吻合程度较好;随着时间的推移,吻合程度越来越差,变化程度越来越剧烈.以上采用的时间步长为0.1,采用不同的时间步长后我们又发现时间步长越小,差分解的精确性越高.我们也可以采用不同的差分格式对此方程进行分析,不同的差分格式在不同的时间段吻合程度不同.
[1]Teman R.Navier-Stokes equations,theory and numerical analysis[M].Studies in Math.and Its Applications No.2.Amsterdam -NewYork-Oxford,North-Holland,1977.
[2]Scheffer V.The Navier- Stokes equations in space dimension four[J].Comm.Math.Phys.,1978(61):41-68.
[3]韩旭里,万中.数值分析与实验[M].北京:科学出版社,2006.
[4]John H,Mathews Kurtis D.Fink数值方法(第4版)[M].北京:电子工业出版社,2005.
[5]袁慰平.计算方法与实习[M].南京:东南大学出版社,2005.
[6]陆会甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,2004:13-18.
[7]余德浩,汤华中.偏微分方程数值解法[M].北京:科学出版社,2003:101-106.
