物料价格随时间波动且考虑返工率的MTO订购决策*
2012-09-12胡盛强张毕西张湘伟李细枚
胡盛强,张毕西,张湘伟,李细枚
(广东工业大学管理学院,广州 510520)
物料价格随时间波动且考虑返工率的MTO订购决策*
胡盛强,张毕西,张湘伟,李细枚
(广东工业大学管理学院,广州 510520)
对于订单式生产(Make-To-Order,MTO)中小型制造企业,物料供应不及时及生产过程产生的不合格品导致生产返工都是影响交货期的主要因素。因物料订购成本占总生产成本的比重较大,当物料价格不稳定时,订购决策人员须综合考虑物料价格的变化趋势以及返工对交货期的影响程度,从而做出成本最低的订购决策。以订单式生产中小制造企业物料订购及不合格品返工为研究对象,考虑物料为多种、物料价格随时间波动且返工率随机时,从提早或延期交货成本角度进行建模与优化以得到最佳订购日期。针对上述问题,构建了有约束条件的多决策变量非线性优化模型,并采用内点障碍罚函数法求解。研究结论表明,在订单式生产模式下,为使与交货期有关的成本最低,物料订购日期不能太早也不能太晚,存在理想值。
订单式生产;价格波动;随机返工率;订购决策
0 引言
对于订单式生产中小型制造企业,当订单下至生产部车间后,生产计划人员依据订单和现有库存向物控部发送物料请购单,并通知工艺部(或研发部)制作工艺标准或要求,当物料(包括原材料和零部件,下同)和工艺要求都到位后,计划人员再根据订单数量和交货期制定详细的生产计划表,生产活动便开始进行。由此可知,在正式投产前,有两项很关键的工作,即物料订购及工艺设计。对于工艺设计,其所需时间一般较固定。而对于物料的订购,若是通用性且价格较稳定的物料可通过库存管理合理储备,若是专用性且价格波动比较大、价值量大的物料(如铜铝等金属材料)则须根据订单要求适时购买以节约订购成本。管理者在某一时刻做出订购决策时,有可能因物料购买太晚而延迟完工从而产生延迟完工成本,也有可能因物料购买太早而产生物料或产成品库存管理成本。生产过程中,由于工人操作不够专注或技术水平不高及设备故障等,容易产生不合格品,为了完成订单需求量,须对不合格品进行返工,返工既需要成本、也需要时间,因此也会影响总成本和交货期。在不同的条件和状态下,返工率表现出了随机性的特点。当物料的订购价格随时间波动且返工率随机时,如何确定最佳的订购日期以使总成本最小是订单式生产中小型制造企业面临的问题之一。
关于价格、交货期或生产提前期的研究,主要有如下研究成果可供参考:Wenting Pan,Kut C.So考虑供应不确定的生产装配系统的零部件数量和价格优化研究,分析了当需求独立于市场价格时,一个零部件的供应不确定是如何影响其他所有零部件的价格和数量的[1]。Shiming Deng等针对制造系统、服务运作系统或供应链分别考虑特定条件下生产数量、物料或终成品价格、交货期或提前期等联合决策问题[2-6]。Timothy L(2009)研究建立了需求不确定性下,基于价格,成本和交货期的关系模型,并通过数值分析验证了模型的有效性[7]。Charnsirisakskul等(2004)建立了一个同时考虑订单接受生产计划和交货期的混合整数线性规划模型,并通过数值计算来检验,并在此基础上加入了价格决策[8]。Hill AV,Hays J M,Naveh E.(2002)研究建立了需求与交货期和价格的关系模型,通过价格与交货期的最优组合实现企业的最大收益的目标[9]。Duenyas(1999)考虑了制造商提出的交货期可能被顾客接受或拒绝,建立了以一定的服务水平为约束,目标值是总利润最大或平均提前期或交货期最短的模型并求解[10]。So Kut C,Song Jing-Sheng(1998)建立了价格、承诺交货期及产能扩张决策的关系模型,分析了各参数变化条件下关于产能扩张的最优决策[11]。黄彬,高诚辉,陈亮考虑完工时间和交货期都是模糊的情况下虚拟企业伙伴的选择问题,以极大化最小客户满意度为优化指标,采用自适应遗传算法对合作伙伴选择模型进行处理[12]。原白云,蔡成元研究对于短生命周期产品在允许缺货情况下,如何设置合理价格折扣来控制订单的流失,确定最佳延迟供货量、最优价格折扣、最优订购时间和订货量,以使总成本最小[13]。狄军峰,俞明南针对价格和交货期相关需求下,含有两个组件的单周期ATO系统,建立了装配商的期望利润最大化的非线性规划模型,求出了最优的产品价格和承诺交货期[14]。林勇,李路军,廖丽平从最基本的通用件库存模型出发,引入承诺交货期-价格因素,研究其对通用件库存策略的影响[15]。刘蕾,罗华,唐小我研究了供应链中供应商和零售商两级间的订货提前期决策问题,在提前期管理成本由上下游分担的条件下,建立了斯坦克尔伯格博弈的订货提前期模型[16]。
上述文献都是从库存、订购价格、订货提前期等方面单一的研究交货期有关决策问题。而本文的主要特点是结合生产实际,综合考虑影响交货期的两大因素,即物料订购和返工率,构建总成本最小化模型,采用最优化方法得到最佳订购决策。
1 模型假设及参数说明
1.1 研究对象及假设条件
(1)在订单式中小型制造企业中,特定客户的订单为单品种、小批量、交货日期明确。生产部接到生产通知单的时间为对订单安排生产的初始时刻,生产通知单上规定的交货期为公司承诺的完工日期,或称为出厂日期。从初始时刻到完工期将经历物料申请、订购及运输时间、排产及生产准备时间(图纸、工艺设计、规格要求等)、正式投产的时间。物料的运输时间及排产、生产准备时间较固定,为其设置固定的生产提前期。
(2)对于不合格品的返工可分为普通返工(即正常上班时间的返工)及应急返工(通过加班或外包进行返工)。相比于普通返工,应急返工的成本高很多,但返工效率更高。
(3)订单所需物料包括价值量相对较低的通用零部件及价值量很高的专用原材料。完成订单所需成本包括订购成本、生产及管理成本、延迟完工或提早完工成本、返工成本。通用零部件的订购及库存、运输成本都归属于生产及管理成本,而订购成本只包含价值量大、价格随时间波动大且波动周期短的原材料订购成本。
(4)对于返工成本,与订单批量及返工率(即不合格品与订单批量的比值)有关。由于员工状态、劳动负荷及技术水平的不稳定,返工率呈连续性随机分布。返工工作由专人负责。
(5)单位时间延期完工成本比单位时间提早完工成本大很多。因此,订购日期与提前期的时间和不能超过承诺完工日期。
1.2 参数说明
根据上述假设条件,针对某订单批量为Q的产品设置有关参数或符号如下:
T0:公司承诺的完工日期。K:专用原材料的种数。Sk:第 k 种原材料的名称(k=1,2,…,K)。Tbk:Sk的订购日期,为决策变量。Tb:最后订购回来的某原材料的订购日期,即Tbk的最大值。Tf:生产提前期,即订购决策日期至正式投产的时间差。Tm:正式投产至实际完工的时间差。Tr:不合格品返工所需的时间,与订单批量、返工率及是否加班有关。γ:返工率。f(γ):γ的概率分布密度。F(z):γ的概率分布函数。E(γ):γ的期望。δ2(γ):γ的方差。Q01:正常工作日的日返工量。Q02:额外加班的日返工量,根据加班时间的长短,令:0<Q02≤2Q01。Cbk:Sk的订购成本,由于价格随时间波动、订单批量确定,则Cbk随时间波动,令:

2 模型构建与求解
由上述假定条件及参数设置,令:Tx=(Tb1,Tb2,…,TbK)(K≥2)可得到关于原材料订购日期决策的最小化总成本模型如下:
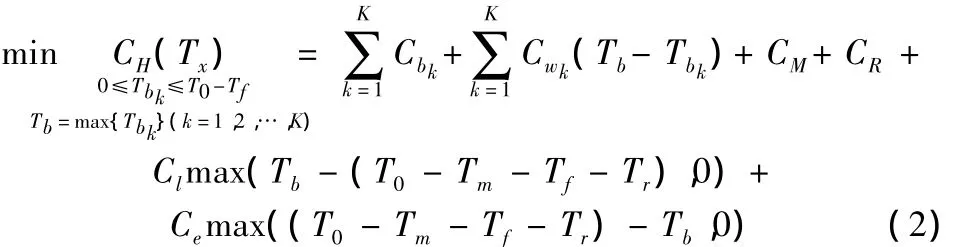
2.1 模型分析
由于γ是随机的,订单需求量Q也是不确定的,当Tb一旦确定下来,对Tr和CR可进行如下讨论(考虑到实际情况,Qγ≤3Q01):若Qγ≤Q01,则Tr=1,CR=Cr1Qγ;若 Q01< Qγ ≤2Q01,决策如下:若 T0-Tm-Tf-Tb≤1,则加班,此时:
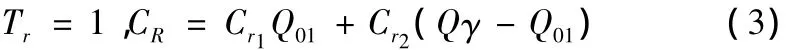
若T0-Tm-Tf-Tb≥2时,则不加班,此时:
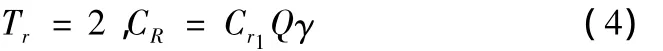
若2Q01<Qγ≤3Q01,决策如下:若T0-Tm-Tf-Tb≤1,则加班,此时:

若T0-Tm-Tf-Tb=2,则加一天班,此时:

若T0-Tm-Tf-Tb≥3,则不加班,此时:

2.2 模型求解及算例分析
2.2.1 模型求解
物料多种时,式(2)可转化如下:
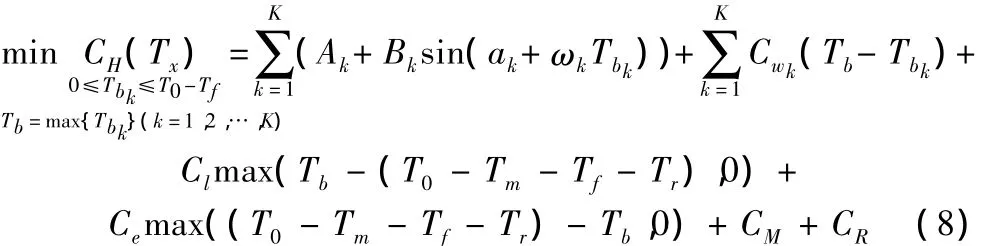
显然,式(8)是一个不等式约束多决策变量非线性约束优化问题,令Tr=1(若Tr=2,也可类似处理)。为求解该问题,先分类讨论:
(1)若最后订购回来的物料的订购日期Tb较晚导致延期完工,即:Tb-(T0-Tf-Tm-1)≥0,式(8)简化为:

对于式(9),采用内点障碍罚函数法,可得近似全局最优解。介绍如下:
该方法的原理是在目标函数上引入一个关于约束的障碍项,当迭代点由可行域的内部接近可行域的边界时,障碍项将趋于无穷大来迫使迭代点返回可行域的内部,从而保持迭代点的严格可行性[17]。步骤如下[18]:
第一步:令 xk=Tbk(k=1,2,…,K-1),xK=Tb,x=(x1,x2,…,xK)。对式(9)关于CH(Tx)及其约束条件转化如下:
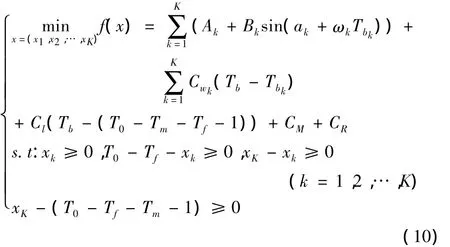
第二步:对数障碍函数p(x;μd)表达如下:
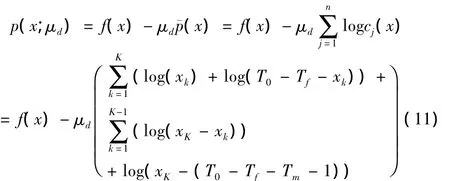
式中,μd为第l次迭代的罚参数,¯p(x)为罚函数,cj(x)为约束函数。
第三步:算法介绍如下:步1:给定初始可行点x0,终止误差0 ≤ ξ≤1,μ1> 0,τ ∈ (0,1)。令 d:=1;步2:以xd-1为初始点求解无约束子问题式(10),得极小点xd;步3:若μd¯p(xd)≤ξ,则终止迭代,并取xd为近似最优解;步 4:令 μd+1= τμd,d:=d+1,转步2。通过上述算法则能得到式(9)的近似最优解。
(2)若最后订购回来的原材料的订购日期Tb较早导致提早完工,即Tb-(T0-Tm-Tf-1)≤0,则式(8)简化为:
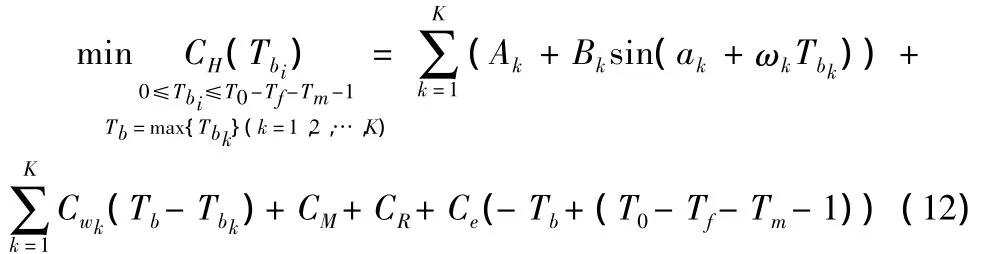
同求解式(9)类似,也可通过上述方法对式(12)求最优或近似最优解。
分情况讨论得到式(9)及式(12)的最优或近似最优解后,再通过比较目标函数值得到式(8)的最优解。
2.2.2 算例分析

3 结束语
对于订单式生产中小型制造企业,影响企业按期交货的因素有很多,如管理不善、生产计划不合理、插单、物料供应不及时、员工请假或短期流失、员工技术不熟练、设备故障等。由于物料订购成本占整个生产成本的比重较大,当物料价格随时间波动时,相关管理人员须综合考虑物料价格的变化趋势及物料购买时间对生产的影响程度,从而尽可能减少总生产成本。本文考虑物料为多种时,物料价格随时间波动且返工率随机时,如何得到最佳订购日期以使总成本最低。在本文的基础上,还有些问题值得继续展开研究,如:订购价格随时间离散随机波动如何进行最佳决策;综合考虑物料订购、员工技术水平、员工流失等因素对交货期的影响如何进行相关决策;考虑订购价格及生产成本与订单数量有关如何进行相关决策。研究这些问题都有相当的实际意义及应用价值。
[1]Wenting Pan,Kut C.So.Optimal Product Pricing and Component Production Quantities for an Assembly System under Supply Uncertainty[J].Operation Research,2010,58(6):1792-1797.
[2]Shiming D,Candace A.Yano.Joint Production and Pricing Decisions with Setup Costs and Capacity Constrains[J].Management Science,May 2006,52(5):741-756.
[3]Pangburn M.S,Stavrulaki E.Capacity and Price Setting for Dispersed,Time-sensitive Customer Segments[J].European Journal of Operational Research,2008,184(3):1100-1121.
[4]Liu,L.M,Parlar M,Zhu,S.X.Pricing and Lead Time Decisions in Decentralized Supply Chains[J].Management Science,2007,53(5):713-725.
[5]Shang,W.X,Liu,L.M.Promised Delivery Time and Capacity Games in Time-Based Competition[J].Management Science,2011,57(3):599-610.
[6]Teimoury,E,Modarres.M,Monfared,AK etc.Price,Delivery Time and Capacity Decisions in an M/M/1 Make-to-order/service System with Segmented Market[J].International Journal of Advanced Manufacturing Technology,2011,57(1-4):235-244.
[7]Timothy L.Establishing Delivery Guarantee Policies[J].European Journal of Operational Resear.ch,2009,196:959-967.
[8]Charnsirisakskul,Griffin P M,Keskinka K P.Pricing and Scheduling with Leadtime Flexibility[J].European Journa1 of Operation Research,2006,171(1):153-69.
[9]Hill A V,Hays J M,Naveh E.A.Model for Optimal Delivery Time Guarantees[J].Journal of Service Research,2000,2(3):254-260.
[10]Duenyas I.Single Facility Due Date Setting with Multiple Customer Classes[J].Management Science,1999,41(3):608-619.
[11]So Kut C.Song J.S.Price,Delivery Time Guarantees and Capacity Selection[J].European Journal of Operational Research,1998,94(3):28-49.
[12]黄彬,高诚辉,陈亮.模糊完工时间和模糊交货期下的虚拟企业伙伴选择[J].北京:系统工程理论与实践,2010,30(6):1085-1091.
[13]原白云,蔡成元.短生命周期产品的延迟交货和价格折扣模型[J]. 广州:工业工程,2010,13(4):53-57.
[14]狄军峰,俞明南.单周期ATO系统的交货期与价格决策模型[J]. 哈尔滨:科技与管理,2010,12(3):30-33.
[15]林勇,李路军,廖丽平.基于承诺交货期与价格的通用件库存模型[J].上海:工业工程与管理,2009,14(5):14-19,30.
[16]刘蕾,罗华,唐小我.基于斯坦克尔伯格博弈的订货提前期决策研究[J].北京:计算机集成制造系统,2007,13(7):1401-1405,1418.
[17]孙文瑜,徐成贤,朱德通.最优化方法[M].北京:高等教育出版社,2004.
[18]马昌凤.最优化方法及其MATLAB程序设计[M].北京:科学出版社,2010.
Ordering Decisions with Materials Prices Fluctuation and Rework Rate under MTO
HU Sheng-qiang,ZHANG Bi-xi,ZHANG Xiang-wei,LI Xi-mei
(School of Management,Guangdong University of Technology,Guangzhou 510520,China)
For the Small and Medium Manufacturing Enterprises about MTO(Make-to-order),materials provision not timely and rework because of non-conforming products generated in the Production process are the major factors which affect delivery time.Due to the material costs accounting for a large proportion of the entire cost,while the materials price is unstable,the decision-makers have to comprehensively consider the price trends and the rework which has a certain impact on makespan so as to make the best decisions about ordering.When the type of materials is more than one,the material price fluctuates over time and the rework rate is random,it considers how to model and optimize to get the best decision of ordering date from the perspective of cost about delivery time,so that the total cost is the lowest.For the problem,it builds a constraint nonlinear optimization model with multi-variables and solves it by the algorithm of IPM.The conclusion shows that,under the mode of MTO,the date of materials ordering can’t be too early or too late(there exists a ideal day)so that the cost about delivery time is the lowest.
MTO;prices fluctuation;random rework rate;ordering decisions
TH165;F27
A
1001-2265(2012)11-0101-04
2012-03-31;
2012-04-12
国家自然科学基金资助项目(71271060,70971026);广东省自然科学基金资助项目(S2012010009278;9151009001000045);广东省普通高校人文社科重点研究基地重大项目(08jdxm63004)
胡盛强(1984—),男,湖南邵阳人,广东工业大学管理学院博士研究生,主要从事工业工程、生产系统组织、控制与优化的研究,(E-mail)hushengqiang54@163.com;张毕西(1954—),男,广东梅州人,广东工业大学管理学院教授,博士生导师,主要从事生产系统控制与优化的研究。
(编辑 李秀敏)
