基于进给系统反馈信号的摩擦辨识方法*

李鹏勃，赵 飞，梅雪松，陶 涛，冯 斌

(西安交通大学机械工程学院，西安 710049)

基于进给系统反馈信号的摩擦辨识方法*

李鹏勃，赵 飞，梅雪松，陶 涛，冯 斌

(西安交通大学机械工程学院，西安 710049)

为了准确辨识进给系统摩擦特性，提高数控机床加工精度，论文以Stribeck摩擦模型作为辨识对象，针对传统的摩擦辨识方法存在的问题，提出了在分析加速运动过程反馈信号的基础上再进行匀速测试的辨识方法。基于该方法进行实验，并使用EMD(Empirical Model Decomposition)方法和最小二乘法对实验数据分析后得到了摩擦模型的参数;实验结果表明文中提出的方法与传统的摩擦模型辨识方法对比，具有操作简单、节省实验时间和辨识准确的特点。

进给系统;摩擦辨识;反馈信号;EMD

0 引言

对于数控机床的伺服进给系统，摩擦环节是提高系统性能的障碍，会使系统响应出现爬行、振荡或稳态误差［1］。为了减小摩擦对数控机床性能的影响，目前主要通过两种方法降低摩擦的影响:一是选择合适的控制策略;二是对摩擦进行补偿，基于摩擦模型的补偿方法是近年来的研究热点，其关键是如何选择一个合适的摩擦模型并且对模型参数进行准确的辨识［2］。Stribeck模型由于考虑了负斜率现象，能够以90%的精度近似拟合低速区域的摩擦力［3］，因此本文选择Stribeck摩擦模型作为辨识对象。

摩擦模型的辨识方法主要有在线辨识方法和离线辨识方法两类。在线辨识是利用系统实时运行中得到的数据来估计摩擦模型，Kaan Erkorkmaz等人利用Kalman滤波器进行了摩擦辨识［4］，李书训采用一种非线性摩擦观测器在线测得摩擦模型［5］。在线辨识的优点是能够实时跟踪系统摩擦模型的参数变化，但缺点是具有摩擦动态辨识功能的控制器设计复杂。离线辨识方法是进行匀速测试实验，然后建立稳态速度和摩擦力的关系。Johnson在没有考虑电机影响的前提下通过实验数据计算得到了黏性摩擦系数和库伦摩擦力值［6］;丛爽通过调整Matlab仿真参数使输出和实际输出一致来辨识模型参数;田政采用最小二乘法进行了辨识［7］。

离线辨识中使用的匀速测试存在一个问题:对于不同的条件，匀速测试时的速度测试范围和测试间距很难选择。因此，有必要寻找确定摩擦非线性区对应速度范围的方法，来合理的规划匀速测试时速度测试范围和间距。为了提高参数的辨识效率和精度，提出了在分析加速运动过程反馈信号的基础上再进行匀速测试的辨识方法。结合EMD自适应滤波数据预处理方法，优化了摩擦参数辨识过程。

1 摩擦模型和辨识原理

1.1 Stribeck摩擦模型简介

摩擦模型分为静态摩擦模型和动态摩擦模型两类。静态摩擦模型包括库伦摩擦模型、库伦+黏性摩擦模型、静摩擦+库伦+黏性摩擦模型、Stribeck摩擦模型等。动态摩擦模型包括Dahl模型、Blimansorine模型、LuGre模型等。

Stribeck摩擦模型和其他摩擦模型相比，具有辨识相对容易，描述摩擦模型比较精确的特点，在伺服进给系统摩擦研究领域得到了广泛应用。C.Canudas de Wit等人使用Stribeck模型实现了自适应摩擦补偿，Kaan Erkorkmaz等人将Stribeck摩擦模型作为摩擦模型进行了前馈补偿研究［4］，冯斌等对一伺服平台用Stribeck模型进行了补偿［8］。

Stribeck摩擦模型描述了摩擦力和相对运动速度之间的关系，表达式［3］如下:

将速度作为横坐标，摩擦力作为纵坐标，得到如图1所示的Stribeck摩擦模型曲线。

图1 Stribeck摩擦模型示意图

主要分为四个区域:静摩擦区域、边界润滑区域、部分流体润滑和全流体润滑。静摩擦阶段，接触面没有相对运动，只有很小的预滑动。边界润滑阶段，驱动力克服最大静摩擦力后开始相对运动，但未形成油膜。部分流体润滑阶段有油膜形成，但接触面并未完全脱离。全流体润滑阶段，油膜将两个接触面分离，黏性摩擦力占主导地位。

1.2 辨识原理

对于滚珠丝杠直线进给系统有如下方程［2］:

在疾病架构中，若不进行手术，疾病无法痊愈，对应于若不进行实质性的改革，经济不会有太大起色，同理，在旅程架构中，若不真正的改变路线和方向，旅途仍会一路坎坷，对应于经济状况不会有太大改善。这些观点源于2008年金融危机后，许多外媒将中国视为世界经济的救命稻草，对中国的经济寄予厚望，而近两年中国经济走势放缓，媒体在报道中则开始“唱衰”。

Tm是电机输出力矩，J为系统等效惯量，B为系统粘滞摩擦系数，ω为电机角速度，Tfc为摩擦力矩。将上式右端第二项粘滞摩擦力矩和Tfc库伦摩擦力矩的和写作Tf，将右端第一项写作Ta，则上式表示为:

当系统匀加速运动时，Ta为定值，上式两端求导得到:

那么可以通过Tm电机力矩的变化来分析摩擦力矩的变化来确定摩擦非线性区对应的速度范围。虽然加速过程中摩擦力矩是变化的，但是控制系统能够使得电机输出力矩跟随负载变化来保持匀加速运动过程。

当系统匀速运动即加速度为0时，Ta为零，那么有:

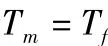
那么测得当前的速度和电机输出力矩就可以得到该速度下的摩擦力矩。

对于力矩，可以采集电机的电流信号或转矩监测信号来得到。对于加速运动过程和匀速运动过程不同时刻的速度，可以借助于对进给系统的位置反馈信号差分得到。

2 摩擦辨识实验

2.1 实验台设计

图2 试验台示意图

2.2 实验方案设计

为了对摩擦模型进行精确的辨识，采用在分析加速运动过程反馈信号的基础上再进行匀速测试的辨识方法。实验分为两个部分:加速测试和匀速测试。

加速测试时，使工作台以一定的加速度做匀加速直线运动，采集运动过程中电机转矩监测信号、工作台光栅反馈信号。然后对采集到的数据进行分析，得到摩擦非线性区对应的速度范围。

匀速测试时，基于加速测试得到的摩擦非线性区对应的速度范围，合理地规划匀速测试的速度测试范围和测试间距;然后使工作台以各个规划速度匀速运行，采集转矩监测信号和光栅尺信号;最后对匀速测试的数据进行处理得到辨识摩擦模型参数所需要的数据。

2.3 加速测试

第一次加速测试中，让系统在3.277s的时间内，速度从0匀速上升到15mm/s。同步采集伺服驱动器转矩监测值Tm和工作台光栅尺位置值Xt。采集到的电机转矩监测信号和差分计算后的速度信号有严重的噪声，如图3所示。

图3 测试噪声曲线

EMD方法作为一种自适应滤波方法具有较好的效果［9］。因此本文采用EMD方法首先对电机转矩信号进行滤波，得到的模式分量如图4所示。

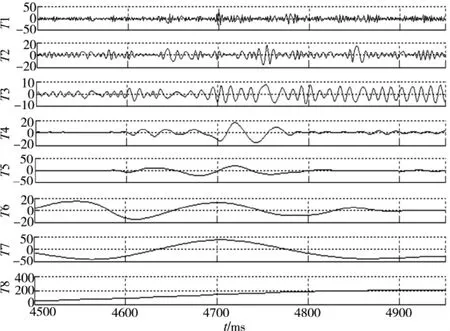
图4 转矩信号的EMD分解结果

由于一、二阶模式分量反映了信号的细节问题，在频域属于高频成分，故而从原始信号中减去一阶和二阶模式分量，将得到的信号作为反映电机力矩的信号，滤波前后信号如图5所示。

对工作台速度信号也进行同样的处理，将其和力矩信号绘制在一起如图6所示。

从图中可以看出，第一阶段:4.618s至4.713s，工作台速度在0附近波动，加速度基本为0，系统处于静摩擦状态。第二阶段:4.713s时刻电机输出力矩克服了静摩擦力矩，系统进入边界润滑状态，虽然电机输出力矩有所减小，但是摩擦力矩也有所减小，故而速度开始增加，加速度基本恒定，但大于设定加速度。第三阶段:从4.726s开始，系统进入部分流体润滑状态，虽然电机输出力矩迅速减少，但摩擦力矩也迅速减少，故而速度继续增加，虽然加速度有所减小，但仍然大于设定加速度。第四阶段:从4.742s开始，系统进入全流体润滑状态，电机转矩和摩擦转矩都随着速度增加而继续增加，加速度在设定加速度附近波动。

图5 转矩信号滤波前后对比

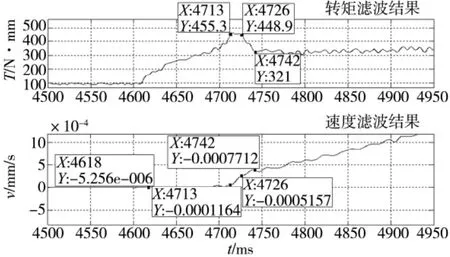
图6 转矩信号和速度信号滤波结果

综上所述，系统克服静摩擦后，在边界润滑和部分流体润滑阶段，电机转矩和摩擦力矩都随着速度的增大而减小;在全流体润滑阶段，电机转矩和摩擦力矩都随速度的增大而增大。电机转矩变化反映了摩擦力矩的变化。那么可以认为部分流体润滑和全流体润滑的分界速度，就是匀加速运动过程中当速度增大，电机转矩不再减小而开始增大的时刻系统的速度。通过求局部极值算法得到4.742s处力矩具有局部最小值，此点之后，电机转矩整体趋势是随着速度增加的，变化过程可以用表1说明。

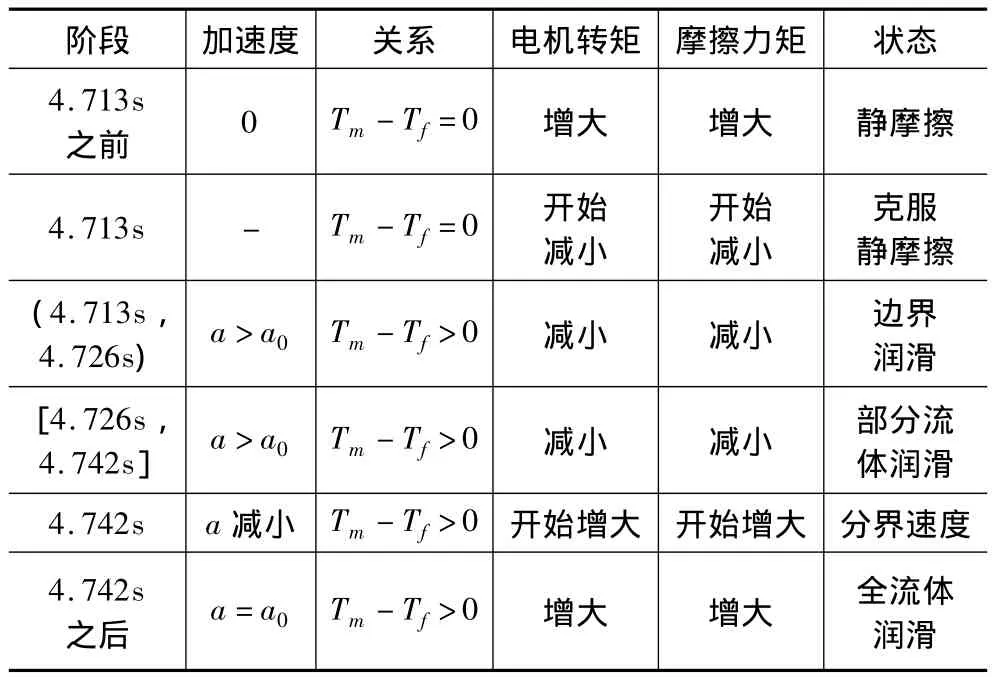
表1 加速过程状态分析

部分流体润滑和全流体润滑转换的时刻为4.742s，对应的工作台在4.740s-4.745s的位置为:0.0079mm，0.0083mm，0.0086mm，0.0090mm，0.0093mm和0.0097mm。此时刻的速度为:0.36mm/s。

再进行三次加速测试，速度分别从0匀加速到7.5mm/s，15.0mm/s，7.5mm/s，对应的润滑状态转换处速度如表2所示。

表2 多次加速测试分析结果

可以认为部分流体润滑和全流体润滑的转换速度在0.2-0.4mm/s之间;系统的摩擦非线性区对应的速度范围为0-0.4mm/s;当速度大于0.4mm/s时，系统工作在摩擦线性区。

通过对多次加速测试过程中伺服进给系统的光栅反馈信号和电机转矩监测信号的分析，不仅得到了系统的摩擦非线性区对应的速度范围，而且基本确定了部分流体润滑和全流体润滑转变的速度。这不仅对于摩擦辨识时的匀速实验设计具有帮助，而且对评价当前的润滑和磨损状态具有一定的参考价值［10］。

2.4 匀速测试

基于加速测试的分析结果:系统的摩擦非线性区对应的速度范围为0-0.4mm/s。进行如下的速度规划:对0-0.4mm/s的速度范围内进行了16次匀速测试，0.4-2mm/s的速度范围内进行了5次匀速测试。

匀速测试中，按规划的速度使工作台运动10s，将光栅尺反馈的总位移值除以时间作为实际速度;将采集到的转矩信号求平均值得到当前速度下的电机输出转矩。由于匀速运动时系统加速度为0，电机输出力矩Tm和摩擦力矩Tf相等。将21次实验数据的处理结果以速度为横坐标，摩擦力矩为纵坐标绘制图形，得到如图7所示结果。

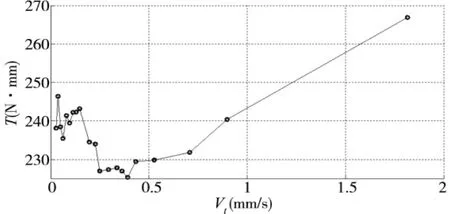
图7 匀速测试获得的实验数据

3 实验数据处理和实验验证

3.1 实验数据处理

首先以0.4mm/s为分界将速度划分为低速段和高速段，然后进行线性拟合，得到以下结果:低速段(v=0-0.4mm/s)方程为:

高速段(v＞0.4mm/s)方程为:

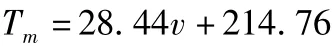
低速段和纵轴交点的纵坐标即为静摩擦力矩，大小为244.16N·mm;高速段和纵轴交点的纵坐标为库伦摩擦力矩，大小为214.76N·mm;高速段斜率即为粘滞摩擦因数:B=0.028N·m/(mm/s);Stribeck模型中的Vs和δ待求。

δ为形状系数，一般在1和2之间选择。通过图8可以知道δ应该选择2，Vs在0.2-0.25之间选择。

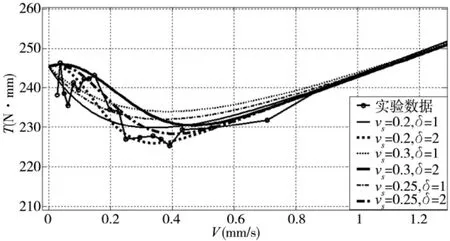
图8 δ和Vs对模型形状的影响

为了求Vs，使用最小二乘法。首先将Vs=0.20，0.21，0.22，0.23，0.24 和 0.25 分别代入模型，然后求出不同速度下模型值与实验测量值的误差的平方和，发现当Vs=0.22mm/s时，平方和最小。所以可以得到摩擦模型为:

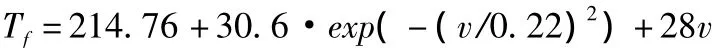
3.2 实验验证

为了验证本文提出的方法的有效性，进行了常规的匀速测试。进行了33次常规匀速测试，并且将实验结果绘制到同一图中，如图9所示，可以发现通过对加速过程中反馈信号分析得到摩擦非线性区对应速度范围后，合理规划速度进行匀速测试的摩擦辨识方法，与传统的匀速测试相比，可以减少实验次数，节省实验时间，辨识准确度相当。

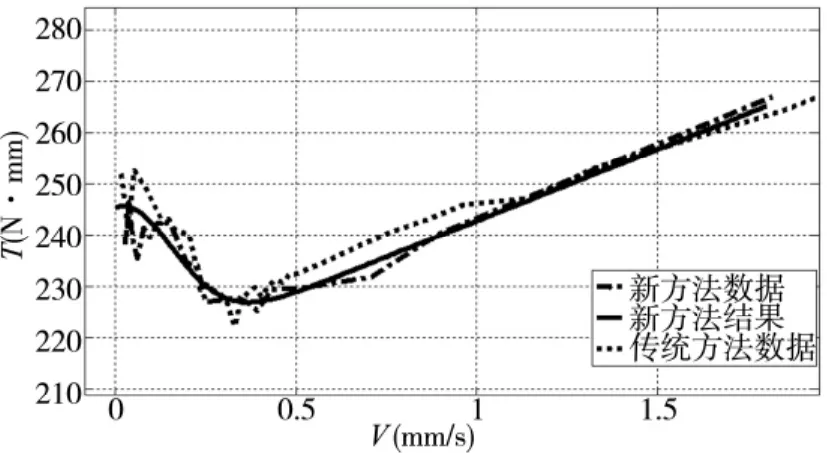
图9 两种方法的对比

4 结束语

本文针对传统的匀速测试方法无法进行速度规划的问题，提出了在分析加速运动过程反馈信号的基础上再进行匀速测试的辨识方法。与单纯的匀速测试方法对比，本文提出的方法既能确定摩擦非线性区对应的速度范围，又能克服传统匀速测试存在的速度无法合理规划的问题，达到节省试验时间，准确地辨识摩擦模型的目的。

［1］刘强，尔联洁，刘金琨.摩擦非线性环节的特性、建模与控制补偿综述［J］.系统工程与电子技术，2002，24(11):45-53.

［2］XS Mei，M Tsutsumi，T Yamazaki，et al.Study of the friction error for a high-speed high precision table［J］.International Journal of Machine Tools＆Manufacture.2001，41:1405-1415.

［3］刘丽兰，刘宏昭，吴子英，等.机械系统中摩擦模型的研究进展［J］. 力学进展，2008，25(5):201-213.

［4］K Erkorkmaz，Y Altintas，High speed CNC system design.PartⅡ:modeling and identification of feed drives［J］.International Journal of Machine Tools＆ Manufacture.2001，41:1487-1509.

［5］李书训，姚郁，马杰.基于观测器的伺服系统低速摩擦补偿分析［J］. 电机与控制学报，2004，4(1):27-30.

［6］Craig T.Johnson，et al.Experimental identification of friction and its compensation in precise，position controlled mechanisms［J］.Transactions on Industry Applications.1992，28(6):1392-1398.

［7］田政.采用限定记忆区间最小二乘法辨识DC伺服系统摩擦非线性参数的方法［J］.信息与控制，1997，26(6):446-473.

［8］冯斌，等.开放式数控系统摩擦补偿的实现［J］.机床与液压，2011，39(19):7-9.

［9］F Zhao，X Mei，et al.Fault diagnosis of a machine tool rotary axis based on a motor current test and ensemble empirical mode decomposition method［J］.Mechanical Engineering Science，2011，225(5):1121-1129.

［10］B.Armstrong，Pierre Dupont and C.Canudas de Wit.A survey of models，analysis tools and compensation methods for the control of machines with friction［J］.Automatic，1994，30(7):1038-1183.

A Friction Identification Method Based on Feedback Signals of Servo Feed System

LI Peng-bo，ZHAO Fei，MEI Xue-song，TAO Tao，FENG Bin
(School of Mechanical Engineering，Xi’an Jiaotong University，Xi’an 710049，China)

In order to accurately identify the friction status of servo feed system and improve the processing accuracy of the numerical control machine，this paper selects the Stribeck friction model and proposes an identification method，which，to solve the problems of the traditional one，uses constant velocity tests based on the feedback signals analysis of servo feed system during the acceleration process.The parameter values of the friction model are acquired through analyzing the experimental data with the EMD and the least square method.The contrast between the proposed method and the traditional one shows the new method is accurate，time-saving and easy to conduct.

servo feed system;friction identification;feedback signals;EMD

TH16;TG65

A

1001-2265(2012)11-0004-04

2012-02-03

国家自然科学基金项目(50875203);国家重点基础研究发展规划资助项目(2011CB706805)

李鹏勃(1988—)男，甘肃人，西安交通大学硕士研究生，研究方向为高速高精度运动控制技术，(E-mail)pengbo_li@126.com。

(编辑 李秀敏)