新型环面蜗杆成形法加工的分析与验证*

张 燕，王君泽，陈厚军，张小萍

(南通大学机械工程学院，南通 226019)

新型环面蜗杆成形法加工的分析与验证*

张 燕，王君泽，陈厚军，张小萍

(南通大学机械工程学院，南通 226019)

新型环面蜗杆副是一种改进的传动形式，基于成形法加工，提出蜗杆廓面加工误差的评定方法，验证实际加工的可行性。利用三坐标测量机的接触式测量方法获得蜗杆廓面上离散点的坐标值，经测头半径补偿、坐标系转换将实际测点和理论测点进行匹配，借助双三次B样条曲面拟合获得实际加工的环面蜗杆廓面，采用法向误差法获得了蜗杆的齿形误差图，并分析了该误差对啮合点的影响。结果表明齿形误差小于0.0021mm，且实际齿形误差图和理论齿形误差图的变化趋势一致，实际啮合点符合设计要求，从而验证了加工方法的正确性。

环面蜗杆;B样条曲面;成形法

0 引言

蜗杆传动广泛应用于汽车、机床、冶金机械和仪器仪表等领域，在实际的蜗杆啮合传动过程中，导致蜗杆发生振动和噪音以及蜗杆使用寿命减少的因素，除了安装误差和受载变形外，另一个主要原因就是齿面的加工误差［1］。因此对加工的蜗杆廓面进行测量和误差评定，以便后续加工的误差补偿显得尤为重要。段振云［2］等利用三坐标测量评定法向圆弧锥齿轮的加工误差，验证了加工方法的正确性和技术的可行性;梁艳［3］借助坐标测量机测量螺旋锥齿轮，并进行数据处理，得到了齿面的误差，为机床参数的调整提供依据;王伏林［4］等针对二维数字化齿面几何特征及加工特点，建立了基于测量的离散阵列式齿面加工误差分析模型，求解出齿面各点的加工误差。

要确定齿面加工误差，仅根据三坐标测量得到的齿面上的离散点坐标，无法直接求解，因此必须将齿面参数化，即利用插值建立齿面的数学模型，确定齿面的参数方程。齿面参数化的方法有多种，孙殿柱［5］等采用B样条方法建立真实齿面数学模型，并进行了误差计算;谷霁红［6］等采用双三次NURBS插值方法拟合，实现了弧齿锥齿轮齿面的重构。

本文针对笔者提出的新型环面蜗杆副中环面蜗杆的加工方法，采用三坐标测量机测得环面蜗杆的齿面离散点的坐标，基于双三次B样条曲面插值原理，拟合得到真实蜗杆廓面，进而求得蜗杆的加工误差，验证加工方法的正确性。

1 新型环面蜗杆及其加工原理简介

为了适应现代传动要求，各种改进型蜗杆传动被不断提出。文献［7］提出了一种新型环面蜗杆副，其结构如图1所示，由蜗杆、钢球和蜗轮三体构成，将传统的滑动副变为滚动副，提高了传动效率。并对蜗杆廓面进行点啮合化处理，降低了传动误差:让廓面的齿形由两个半径为r的偏置圆弧和齿根圆弧组成，主齿形r与钢珠之间的半径差Δr为齿形圆心与钢珠中心在指定压力角αn方向上的偏移量(见图2)。蜗杆廓面由处在准线法平面内的齿形沿准线作单自由度运动扫掠所形成的法向圆弧螺旋面，且左右齿形的对称线始终保持在环面法向上。

这种新型环面蜗杆尚没有人提出合适的加工方法进行实际加工，笔者在对该蜗杆廓面进行理论研究的基础上，提出了基于准线的成形法加工方法，并在文献［8］中对该方法存在的原理性误差进行理论推导计算，结果表明成形法加工存在的原理性误差在合理的范围内。本文旨在采用该方法进行实际的切削加工，并借助三坐标测量、B样条曲面拟合等得出实际的加工误差，进一步验证基于准线的成形法加工方法的实际可行性。

图1 环面蜗杆副

图2 蜗杆齿形

由廓面的形成过程可知，齿形与廓面准线间的关系较为单纯，这就为成形法加工提供了便利。在加工过程中，若采用刃形与齿形相同的指状铣刀，使刀心沿着廓面准线移动，且刀轴也始终保持在环面的法向方向，这就确保了刀具与蜗杆毛坯件之间的相对运动与蜗杆传动时的运动一致，也就使刀具刃形包络出的蜗杆廓面在最大程度上与理论廓面接近。当环面蜗杆的主要设计数据如表1所示时，根据啮合原理得到的理论齿形误差如图3所示［8］。图4是在五轴数控铣床上用成形法实际加工蜗杆的场景。下文利用三坐标测量机具体测量蜗杆廓面，并分析计算成形法加工该蜗杆的实际误差。

表1 环面蜗杆的参数

图3 理论齿形误差图

图4 五轴数控铣床加工蜗杆

2 齿面数据测量

2.1 测量方案

根据工件特点，从测量精度和数据后处理等方面综合考虑，采用三坐标测量机采集数据，如图5所示。三坐标测量机型号为MQ8106，接触式打点，采用的测针直径为2mm并对其进行校正，测量所用到的A0B0测针形状误差仅为0.0002mm。蜗杆加工表面为曲面，曲面有显式、隐式和参数三种表示方法，参数曲面更便于表示和构造。一般参数曲面，由u，v两个参数表示。测量环面蜗杆时，以齿形方向为u方向，以螺旋线方向为v方向测量，将测量点数据保存为.asc的格式。

图5 三坐标测量蜗杆

2.2 半径补偿

三坐标测量所得的坐标点是其测头中心的坐标，当被测面为平面时，实际接触点与测头中心相差一个测头半径r，可通过三坐标的自动补偿功能进行调整。本文中所讨论的蜗杆廓面为复杂曲面，测量时测头与蜗杆齿廓面的实际坐标的关系如图6所示，输出的是测头中心坐标点P，自动补偿将得到P1点，而实际测点为P0，因此需对输出的坐标点进行换算。测头所在曲面的单位法矢为:

实际测点的坐标为:

图6 测头坐标与实际坐标关系

3 双三次B样条曲面拟合

3.1 流程

根据上述测量点的坐标，拟合B样条曲面的流程如下:

(1)读入测量点坐标;

(2)根据测量坐标系和设计坐标系的关系，进行坐标转换，将测量点的坐标值转换为设计坐标系下的坐标值;

(3)将转换后的坐标值作为B样条曲面的型值点，按照B样条曲线的反求公式，反求出u方向的控制点，将其作为v方向型值点，再次反求，得到双三次B样条曲面的控制点;

(4)根据双三次B样条的正求算法，求解B样条曲面方程;

(5)以u、v为变量，求拟合的B样条曲面上若干个点的坐标，以便求解理论蜗杆廓面和实际蜗杆廓面之间的误差。

3.2 齿面坐标转换

式中，Tt是沿坐标轴的平移矩阵;Tα、Tβ、Tγ分别是绕X、Y、Z轴的旋转矩阵。

图7 坐标系转换关系

3.3 双三次B样条曲面反求

根据蜗杆廓面上的测点(型值点)求出相应的特征多边形，然后生成由特征多边形网格顶点(控制点)控制的B样条曲面，这就是B样条曲面反求控制点的问题。蜗杆廓面的测点共m*n个，本文采用曲面反求控制点的双向曲线反算法，即:取u方向的m组型值点，按照B样条曲线反求控制点的公式及边界条件，得到m组(n+2)个控制点组成的特征多边形;再将上述控制点当作v方向的型值点，反求出(m+2)*(n+2)个控制点组成的特征多边形，即为双三次B样条曲面的控制点。

由三次B样条曲线的端点性质可知，型值点Pi和控制点bi(i=1，2…n)的关系为:

上式中的型值点比控制点少两个，因此反求时，需加入两个边界条件。常用的方法有:给出起点和终点的切线方向，两端点各外延增加一点，或利用端点的重点。本文采用了第三种方法，即利用重点技巧:P1=b1，Pn=bn。则B样条曲线反求控制点的线性方程组为［9］:

公式(5)是对三角方程组，可用追赶法进行求解。利用重点性质，两端各加两个控制点:

至此，求出了u方向B样条曲线的所有控制点。类似的求出v方向的控制点，则B样条曲面反求工作完成了。

3.4 正求算法

由反求算法得到双三次B样条曲面的控制点后，再根据B样条曲面的正求算法，由控制点求出曲面方程，即可进行B样条曲面拟合。B样条曲面拟合的方程为［10］:

式中，bij是u，v两个方向上的控制点。

拟合后的B样条曲面是含u，v两个参数的多项式方程。使参数u，v在［0，1］之间变化，便可得到拟合的B样条曲面上任意点的坐标值，方便求解理论蜗杆廓面和实际蜗杆廓面的误差，检查加工方法正确与否。

4 精度计算

计算误差的方法有四种:弧长法、弦长法、最小距离法、法向法［4］，但只有法向法求得的误差才是真正的齿形误差，其他的均是基于小偏差和小误差假设条件下齿形误差的近似值，且法向法使用最为广泛，故本文采用法向法求解。由理论蜗杆廓面上的节点S沿其法向量方向求实际廓面的相应节点S'，S与S'之间的距离即为理论点和测点的法向误差ε，如图8所示。

根据上面的公式，计算所得的蜗杆的法向误差的部分数据如表2所示，其中齿形圆弧极角θ为齿形上点的径向线与水平方向的夹角。由表可知，法向误差范围为0.0019～0.0021mm，误差量级较小，符合蜗杆加工要求。蜗杆齿形误差如图9所示，点划线、虚线、实线分别是蜗杆喉圆、蜗杆与钢球啮入、啮出区域的齿形误差，与理论得出的齿形误差图趋势一致，验证了加工方法的正确性。

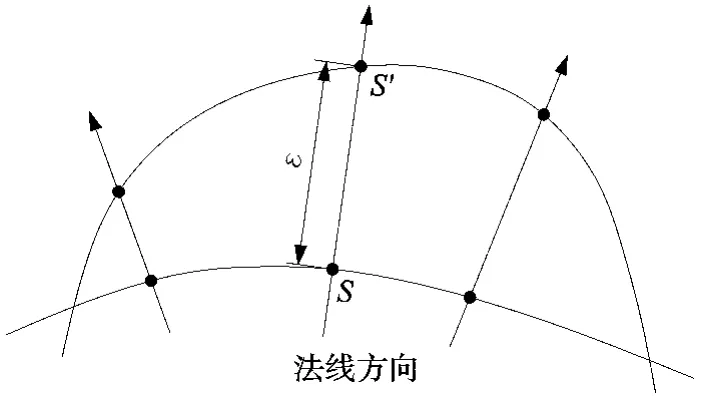
图8 法向误差

表2 实际加工误差值

图9 实际加工的齿形误差

5 加工误差影响

上面的计算的齿形误差对蜗杆副的啮合点是否存在影响，即:蜗杆副是否仍在设定的压力角处啮合，以及如若存在影响又是在何处啮合，这些都是有必要进行讨论研究的。

蜗杆副实现了蜗杆、钢球和蜗轮的三体啮合，蜗轮的加工等问题不在讨论的范围之内，因而只研究蜗杆和钢球的啮合问题。钢球的球心在蜗杆的准线上，传动时钢球和蜗杆廓面啮合，因而蜗杆和钢球的啮合点位于离蜗杆准线的一个钢球半径的地方。因而我们只需要采用零间隙法原理［1］，不断记录离蜗杆准线一个钢球半径位置处且位于蜗杆廓面上的点的坐标，是否在原先设定的压力角处，若不在，是否偏差较大即可。根据上面的原理，求得实际啮合点的压力角在24.987～25.015°之间，表1中设计的压力角为25°。结果表明，压力角的变动范围较小，符合原始设计的要求，验证了采用上述成形法加工蜗杆廓面并不改变传动原理的设计思想。

6 结论

本文通过三坐标测量机测量了环面蜗杆廓面上点的坐标，基于双三次B样条曲面拟合原理，以测点为型值点反求B样条曲面的控制点，拟合得到B样条曲面。在理论蜗杆廓面的法向方向求解对应的实际测点，得到蜗杆的齿形误差，结果表明采用该方法加工蜗杆精度高，符合实际的需要，进一步验证了加工方法的正确性，为后续误差补偿提供了依据。

［1］孙殿柱.真实齿面啮合理论［M］.北京:科学出版社，2006.

［2］段振云，金映丽，李强.基于三坐标测量的法向圆弧锥齿轮的误差评定［J］.沈阳工业大学学报，2003，25(5):364-366.

［3］梁艳.三维坐标测量机实现螺旋锥齿轮测量的研究［J］.机械与电子，2009(19):465-466.

［4］王伏林，易传云，杨叔子，等.二维数字化齿面加工误差分析［J］. 华中科技大学学报，2003，31(11):55-57.

［5］孙殿柱，董学朱.描述真实齿面数学模型的研究［J］.农业机械学报，2000，31(1):79-81.

［6］谷霁红，李建华，樊红卫，等.弧齿锥齿轮测量齿面的NURBS重构［J］.机械与电子，2010(2):41-43.

［7］陈厚军.蒙日曲面共轭原理与环面蜗杆珠轮传动技术的研究［D］.大连:大连理工大学，2009.

［8］张小萍，陈厚军，王君泽，等.成形法加工新型环面蜗杆的原理性误差分析［J］.机械设计，2011，28(12):44-47.

［9］应道宁，吴中奇，王尔健.计算机绘图［M］.浙江:浙江大学出版社，1995.

［10］张义宽，张晓滨，耿楠，等.计算机图形学［M］.西安:西安电子科技大学出版社，2010.

The Analysis and Verification for the Forming Method of Novel Toroidal Worm

ZHANG Yan，WANG Jun-ze，CHEN Hou-jun，ZHANG Xiao-ping
(School of Mechanical Engineering，Nantong University，Nantong 226019，China)

The novel toroidal worm pair is an improved type of transmission.Based on the forming method，the method of error assess of worm surface is put forward to verify the feasibility of the machining method.The actual coordinates，which are obtained by contact measurement of the three-coordinate instrument，are matched with theoretic coordinates with the radius compensation and coordinate conversion.The actual surface is fitted by bicubic B-spline surface，the sketch of the tooth profile error is obtained with the method of normal error，and the impact of error on the meshing points is analyzed.The results show that the tooth profile error is less than 0.0021mm，the trend of the actual tooth profile is consistent with theoretic，and the actual meshing points also meet the design requirement，thus verifying the correctness of machining methods.

toroidal worm;B-spline surface;forming method

TH132.44

A

1001-2265(2012)11-0021-04

2011-12-27;

2012-04-12

国家自然科学基金资助项目(51105210);南通大学自然科学研究项目(10ZY006)

张燕(1987—)，女，江苏扬州人，南通大学机械工程学院硕士研究生，研究方向为数字化制造与工程信息处理技术;通讯作者:王君泽(1949—)，男，江苏南通人，南通大学机械工程学院教授，硕士，研究方向为数字化设计与制造技术，(E-mail)wnag.jz@ntu.edu.cn。

(编辑 李秀敏)