数控微磨床热误差的时序分析法建模及应用*

舒启林，李玉龙，吕玉山

(沈阳理工大学a.汽车与交通学院;b.机械工程学院，沈阳 110159)

数控微磨床热误差的时序分析法建模及应用*

舒启林b，李玉龙a，吕玉山b

(沈阳理工大学a.汽车与交通学院;b.机械工程学院，沈阳 110159)

提出了采用时间序列分析法进行数控微磨床热误差建模的基本原理及方法，及其在微磨床热误差补偿建模中的应用。使用实时过余温度序列建立时序分析模型并进行预测。再通过由微机和微磨床控制器构成的补偿系统，根据建立的时序分析模型，由微机算出补偿值送入微磨床控制器，对砂轮进行附加进给运动。通过对热误差补偿模型补偿效果的分析，证明了以实时过余温度为自变量的时序分析法在数控微磨床热误差建模中的有效性与可行性。

时间序列分析;实时过余温度;热误差建模;误差补偿

0 引言

最近几年，在一些先进机械产业，如军事、航空航天及生物医药产业中，普遍期望设备能够更精巧，更加容易操作，因而构件的微型化是有待解决的主要问题。这样，就需要一种能加工出微小复杂构件且精度较高的设备，因此，桌面微磨床的研制是十分必要的。本文以自行设计的数控微磨床为研究对象。该数控微磨床用于具有多样化材料和三维复杂结构的微小构件以及微机械零件的加工，是以半导体技术为基础的一种微机械加工制造技术。该微磨床主要由超高转速的磨削主轴和工件主轴、自动微砂轮交换系统、伺服控制的微纳米进给工作台、微冷却系统、CCD图像高精密数控系统、识别监测系统所组成。完成对各种微轴类(φ100～1000μm)零件、孔类零件的磨削制造，其三维结构如图1所示。

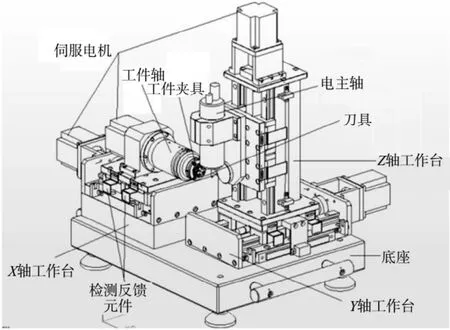
图1 数控微磨床结构图

在微磨床磨削过程中，由于微磨床各部件温升引起的热变形，使微磨床上砂轮与工件之间的位置产生了变化，进而产生了加工误差。研究表明，热误差是微磨床的主要误差源，因此对热误差的控制是提高数控微磨床加工精度的关键。微磨床热误差在很大程度上是由于加工周期、加工条件、冷却液的使用及周围环境变化等因素而产生，而且热误差显示出非线性及交互作用。通常根据统计学理论对微磨床热误差数据和相关温度变化作相关分析，用最小二乘法进行拟合建模，但是很难精确建立热误差数学模型［1］。

本文在研究了国内外磨床热误差模型建立情况的基础上，根据自行设计的数控微磨床的热误差特性，提出了下面用于微磨床热误差建模的时序分析建模法，即采用时间序列分析方法对有规律的动态信号进行整理、分析与研究。用AR(自回归)模型拟合数控微磨床热误差与相关关键点过余温度［2］之间的关系，揭示数据本身的结构与规律，提取数据序列中所蕴含的信息，掌握数据序列内在的变化特点，熟悉有关系统的特性，从而达到控制规律，进而预测微磨床热变形误差的变化规律。故大大提高了热误差模型的精度和补偿系统的鲁棒性。

1 时序分析建模及应用研究

1.1 最小二乘法建模

对如1图所示的数控微磨床进行热误差建模及补偿研究。由于该数控微磨床的独特结构，其在热源分布、对温度的敏感位置及热变形特征上也有其特殊性。通过对该微磨床的温度测点的合理布置，热源分布、热变形分析研究后，得出在确保热误差模型精度的情况下，只需要在该微磨床上的4个关键温度测点［3］放置温度测试仪，减少了温度变量的数量和建模所需的时间。这4个关键温度测点依次是砂轮主轴Ts，冷却液 Tl，液压油 Ty，工作台 Tg，其中砂轮主轴温度Ts对微磨床热误差的影响最大［4］。为方便实际生产应用，热误差数学模型的估计式采用线性模型，其形式如下:

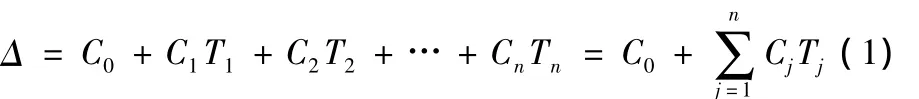
(1)式中，为热误差(由微磨床热变形引起的砂轮与工件位置偏差)，Tj为微磨床上j点位置的温度，C0为常数，Cj为温度系数。

联系本课题，以实时过余温度为自变量，该微磨床热误差数学模型为:

(2)式中，r为微磨床主轴径向热误差(零件径向尺寸有较高的精度要求，本文只考虑微磨床主轴的径向热误差)，生产应用中为随微磨床温度变化而变化的零件径向尺寸误差;C0、CS、Cl、Cy和 Cg为相应的温度系数。

1.2 时序分析建模

时序分析法简而言之是指采用参数模型对现有的有序随机数列进行研究和处理的一种数列处理方法。非常适合用于那些输入不能确定或不可预测的研究对象的描述，因为时序分析是建立在输出相等的条件上，即时序模型所表述的系统与现实系统只需要输出相等，可对输入不能接近的输出序列进行建模，因此可以将此方法用于微磨床热误差建模［5］。

应用时间序列建模，首先要建立ARMA(滑动自回归)模型，对于平稳的、均值为零的时间序列{xt}，可以建立随机的、线性的差分方程，即

(3)式中，θt为滑动平均系数，xt为时间序列{xt}在t时刻的元素，at为残差，φt为自回归系数。

(3)式就是p阶自回归q阶滑动平均混合模型。ARMA(p，q)时序模型能够转化成两个特殊模型:AR(p)模型和MA(q)模型。因为自回归AR模型的模型参数估计比较准确，所需计算量小，建立步骤比较简单，所以比较适用于数控微磨床热误差补偿建模。此外，可通过逆函数，用可能是无穷阶的自回归AR模型来靠近ARMA模型。因此，选用自回归AR模型来预测数控微磨床热误差。

对于 AR(n)模型 xt= φ1xt－1+ φ2xt－2+ … +φpxt－p+at，要求数据是均值为零的、平稳的随机序列。平稳的时间序列应该有不随时间变化的方差、均值和自相关函数，且该序列的自协方差函数只和时间的间隔长短有关，而与此间隔时间点的位置无关。序列是否平稳可以先用统计方法来验证。对具有不确定性部分的时间序列，在进行建模前应先剔除不确定性成分，然后将剩余平稳的随机序列进行时间序列建模。

下面针对该微磨床加工中心实施时间序列建模研究，在此微磨床加工中心实际磨削过程中采集所需数据。由于该微磨床热误差数值和4个关键点的过余温度值之间有着明显的变化规律，显而易见不是一个平稳的序列，假如直接用最小二乘法来拟合进行预测，其偏差通常很大。所以必须对该时间序列进行平稳化处理，即把非平稳的趋势部分剔除出去，然后对剩余平稳部分用时序分析进行拟合，可以采用下述模型:

(4)式中，xt为平稳零均值的随机部分。f(t)为模型的确定性部分，可以看做是最小二乘法的数学模型，这部分是序列随时间而变化的平均值表现了时间序列的变化规律。因此叠加模型为:

(6)式中，yt为微磨床径向热误差，TSg=TSTgTlg=Tl－Tg，Tyg=Ty－Tg为相应的实时过余温度变量，xt为该序列的残量。

利用 matlab 的［b，bint，r，rint，stats］=regress(Y，X)函数［6］计算出C0、CS、Cl、Cy的最小二乘估计b，残量xt。

依据最小最终预报误差准则判定，残量{xt，}服从AR(1)模型:

依据自协方差函数的样本估计值:

依据自相关函数的样本估计值:

其中，k=0，1，2，…(N－1)。

通过解Yule-Walker方程，得出AR(1)模型的自回归系数的估计值:

{at}方差的矩估计:

通过比较得知，利用AR(1)模型得出的残差平方和RSS相对于最小二乘估计模型得出的残差平方和RSS下降很多，表明模型得到改进。于是模型叠加后为:

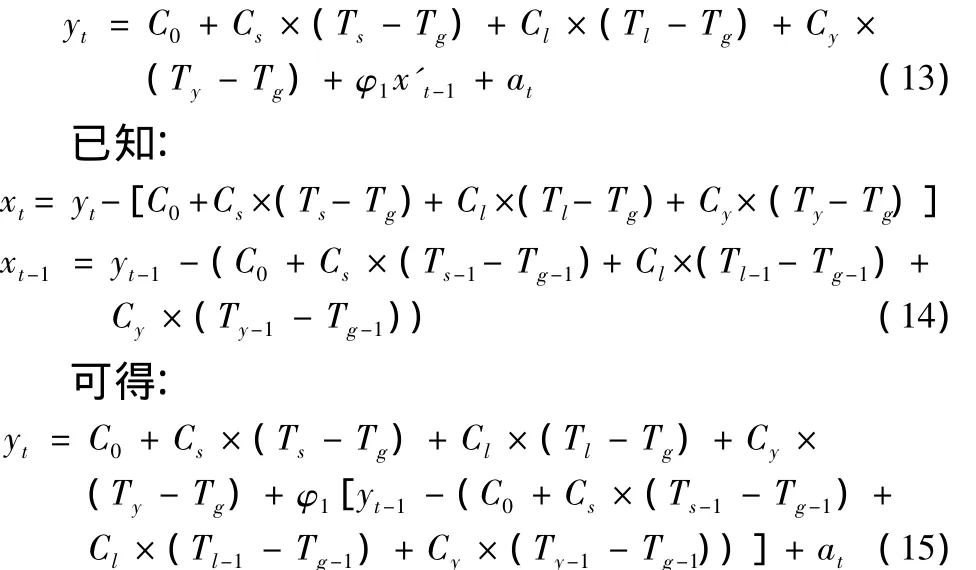
分别将参数C0、CS、Cl、Cy和φ1的值代入(15)式中，最终得到该微磨床主轴径向的热误差时间序列模型，其预测模型为:

2 热误差补偿系统

如图2所示，该补偿系统由TC-3型多路温度测试仪(通过温度测试仪优化布置研究后，布置在磨削中心的4个关键温度点［7］上)，A/D板，具有桥接功能电路的调整板及结合磨削中心的控制器构成。首先借助布置在磨削中心上的4个温度传感器实时采集磨削中心的温度信息。然后，信息由调整板去噪、调整、放大等处理后再通过A/D板进入磨削中心的控制器［8］。控制器依据建立的热误差时序数学模型计算出需要补偿的数值，对砂轮的进给运动进行实时监测与控制，达到修正微磨床热误差的目的。

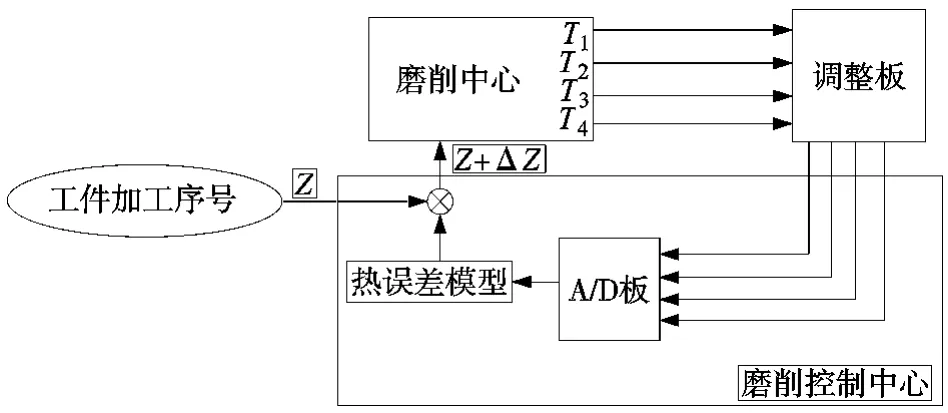
图2 补偿系统模型

3 热误差补偿方案补偿结果

根据多元线性回归理论和时序分析法，运用最小二乘法和时序分析法建立热误差补偿模型，使用实时过余温度为模型变量，得出微磨床热误差预测曲线图。

表1 两种模型预测残差指标对比

图3，图4分别是以实时过余温度为变量建立的最小二乘模型和时序分析模型微磨床热误差补偿效果。表1是以实时过余温度为变量的最小二乘模型和时序分析模型的残差量的对比。通过对补偿效果的观察和数据结果的分析，可以看出以实时过余温度为变量的时序模型，比一般的最小二乘法建模精度要高，补偿效果更好。

图3 实时过余温度变量最小二乘模型补偿效果

图4 实时过余温度时序分析模型补偿效果

4 结束语

本文重点论述了时间序列分析法在数控微磨床热误差补偿建模中的应用。选用实时过余温度为变量建立时序模型，并与最小二乘建模方法进行了模型对比。结果表明，应用本文论述方法建立的时序模型能够显著提高热误差建模精度。

［1］李永祥，童恒超，杨建国.数控机床热误差的时序分析法建模及应用［J］.四川大学学报，2006，38(2):77-81.

［2］张良，王德伦.加工中心热误差补偿技术的研究［D］.大连:大连理工大学，2009.

［3］Yang Jianguo，Pan Zhihong.Application of regression orthogonal design in thermal error modeling of machine tools［J］.Aviation Precision Manufacturing Technology，1999，35(5):33-37.

［4］盛晓尘，杨建国.数控磨床热误差实时补偿控制系统研制及应用［D］.上海:上海交通大学，2006.

［5］张琨，姚晓栋，张毅，等.基于时序模型优化选择的热误差建模［J］.组合机床与自动化加工技术，2011(10):36-39.

［6］黄忠霖.控制系统MATLAB计算及仿真［M］.北京:北京国防工业出版社，2001.

［7］Ching-Wei Wu，Chia-Hui Tang，Ching-Feng Chan-g，Ying-S-hing Shiao.Thermal error compensation m-ethod for machine center［J］.Manuf Technal，2012(59):681-689.

［8］Xin-hua YAO，Jian-zhong FU，Zi-chen CHEN.Bayesian networks modeling for thermal error of numerical control machine tools［J］.J zhejiang Univ Sci A，2008，9(11):1524-1530.

Application of Time Series Analysis to Thermal Error Modeling on NC Micro-grinder

SHU Qi-linb，LI Yu-longa，LV Yu-shanb
(a.School of Automotive and Transportation Engineering;b.School of Mechanical Engineering，Shenyang Ligong University，Shenyang 110159，China)

Using the method of time series analysis in thermal error modeling on NC micro-grinder，presenting its basic principle and method and the application in thermal error compensation of NC microgrinder modeling.How to utilize the real time excess temperature variables surveyed to model and predict was discussed in detail.The compensation system was composed of the computerand the controller of micro-grinder.The controller of micro-grinder，making use of the compensating values computed by the computer through time series analysis model established，ordered grinding wheel resta additional movement realize the real time compensation of micro-grinder thermal errors.Basing on the thermal error compensation model compensation effect analysis.Therefore，the feasibility and validity of real time excess temperature variables in the application of thermal error modeling on NC micro-grinder have been proved.

time series analysis;real time excess temperature;thermal error modeling;error compensation

TH122

A

1001-2265(2012)12-0030-03

2012-04-13;

2012-05-15

辽宁省工业攻关计划资助项目(2011220009)

舒启林(1969—)，男，沈阳理工大学机械工程学院教授，工学博士，博士后，研究方向为先进数控技术，现代设计理论与方法等，(E-mail)shuqilin@139.com。

(编辑 李秀敏)