PMSM控制器参数自整定研究*

牛永岭，皮佑国

(华南理工大学自动化科学与工程学院，广州 510640)

PMSM控制器参数自整定研究*

牛永岭，皮佑国

(华南理工大学自动化科学与工程学院，广州 510640)

文章研究永磁同步电动机(Permanent Magnet Synchronous Motor，PMSM)转速电流双闭环控制系统控制器参数的自整定方法。电流环根据辨识得到对象参数按照工程设计方法进行整定。速度环采用模糊自整定的方法。根据速度响应的超调量和调节时间，经模糊化、模糊推理和清晰化得到控制器参数调整量，从而改变速度控制器参数，直到满足指标要求，最后将参数固定。实验表明，该方法改善了速度响应性能，实现了永磁同步电机安装后伺服驱动控制器参数的快速自整定。

PMSM;工程设计;模糊自整定;PID控制器

0 引言

永磁同步电机具有体积小、效率高、调速性能好的优点，由其组成的交流伺服系统在数控领域得到了日益广泛的应用［1］。PMSM一般采用转速-电流双闭环控制。由于PID控制器结构简单、鲁棒性好，控制器一般采用PID控制器。

PMSM型号多种多样，电机所连接的负载的类型和大小也不尽相同。电机新安装或负载变化后，必须对PID控制器的参数进行调整。人工调整PID参数需要根据经验，费时费力。Ziegler和 Nichols［3］提出根据对象阶跃响应，按照经验公式整定，计算简单但参数仍需调整。文献［4］介绍了由庄敏霞和Atherton提出的最优整定方法。文献［5］提出遗传算法PID整定方法，将遗传算法的并行运算和自适应的特点应用到PID整定中。文献［6］将模糊推理方法与PID相结合，根据误差及误差变化在线调整PID参数。在电机和负载确定后，对象参数基本保持不变，而且DSP运算能力有限，同时为了保证多轴联动时速度响应的同步性，不宜采用复杂的在线整定方法整定PID控制器参数。

本文研究PMSM控制器参数的离线整定即电机在机械设备上安装后的驱动系统控制器的参数自整定。首先根据辨识电流环对象参数和电机参数按工程设计方法整定电流控制器和速度控制器参数。由于工程设计方法得到的速度响应超调大、调节时间较长，设计速度控制器参数模糊整定。以速度阶跃响应的超调量和调节时间为输入，根据PI参数对系统响应的影响及人工调整经验制定模糊规则表，经模糊化、模糊推理和清晰化得到控制器参数的调整量，离线调整控制器参数，直至满足指标结束整定。

1 控制器参数的工程设计方法

永磁同步电机本身是一个高阶、非线性、多变量、强耦合的对象，采用矢量控制id=0控制策略在dq坐标系下电机的数学模型等效为他励直流电机模型。双闭环调速系统的工程设计方法经过合理的简化处理，将系统近似为低阶系统。根据典型I型和典型II型系统参数与性能指标之间的关系确定控制器参数。整定过程中，先设计电流控制器，然后把整个电流环作为转速环的一个环节，再设计转速控制器。

1.1 电流控制器参数整定

电流环作为系统的内环，其主要作用是跟随电流指令变化，应将电流环设计成I型系统。经过简化与近似后电流环模型如图1所示，电流控制器采用PI控制器。其中，β为电流反馈系数，KPWM为逆变器放大倍数，R为电枢电阻，Tl为电气时间参数，T∑i为电流环小惯性群时间常数，ki和τi分别为电流控制器比例系数和积分时间常数。其中T∑i=TPWM+Toi，TPWM为逆变器惯性时间参数，Toi为电流滤波时间常数。

图1 PMSM电流环模型

在电流环对象参数辨识中，取Toi=0，TPWM取逆变器开关周期的一半，远小于Tl，电流环对象可近似为一惯性环节。设置电角度为一固定值，电机不转排除了反电势的影响。实验中通过vq-iq响应曲线得到电流环对象比例KI=βKPWM/R，惯性时间常数TI=Tl。

为将电流环设计成I型系统［7］，应将对象中大的时间常数Tl与控制器零点抵消掉，即:

根据I型系统动态性能指标，兼顾电流超调量和调节时间，取:

1.2 速度控制器参数整定

为了转速无静差，抑制负载扰动和速度波动，速度控制器采用PI控制器，将速度环整定成典型Ⅱ型系统。PMSM速度环控制系统框图如图2所示，图中把电流环简化为一阶惯性环节并与转速环滤波合并等效为速度小惯性环节。其中，kn和τn分别为速度PI控制器增益和积分时间常数，T∑n为速度小惯性时间常数，J为电机转动惯量，α为转速反馈常数，KT为转矩系数。

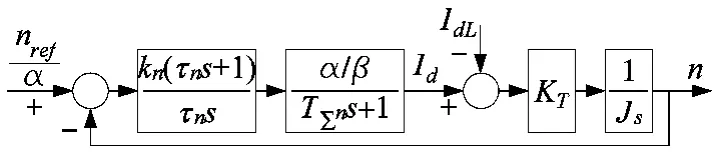
图2 PMSM速度环模型

根据典型Ⅱ型系统参数和系统性能指标的关系，选取中频宽h=5:

此时按线性系统计算有转速超调σn=37.6%，调节时间ts=9.55T∑n。虽然考虑控制器饱和，超调有所下降，但仍难以满足要求，必须对转速控制器参数进行调节。

2 速度控制器参数模糊自整定

在电机或负载变更后，经过工程设计方法得到控制器参数不能满足要求。为了保证系统速度响应性能，必须对速度控制器参数进行调整。速度控制器参数模糊自整定框图如图3所示。根据速度阶跃响应曲线得到超调量和调节时间，经模糊化接口进入模糊推理。模糊推理采用Mandani模型，根据建立的模糊规则得到推理结果。最后经过清晰化得到PI参数调整量的精确值，进而改变速度PI控制器参数。

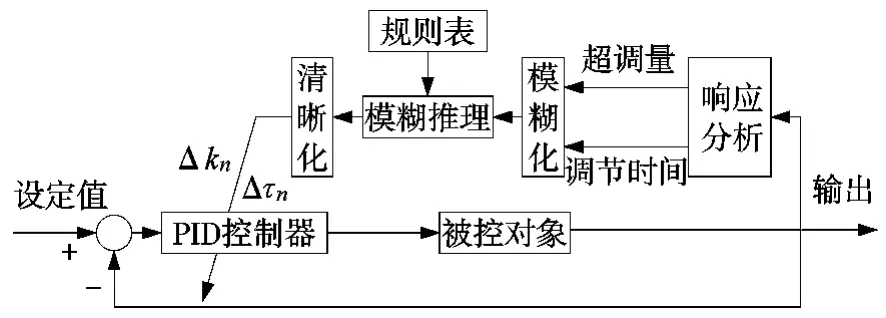
图3 速度控制器参数模糊自整定框图

2.1 隶属度函数

选择系统阶跃响应的超调量σ和调节时间ts作为模糊运算的输入量，PI控制器参数kn、τn的调整量Δkn、Δτn为输出量。由于超调量和调节时间的非负性，输入模糊集和论域是非对称的。超调量σ的论域为:{0，5%，10%，15%}，其模糊集为:{PZ，PS，PM，PB};调节时间ts的论域为:{0s，0.25s，0.375s，0.5s}，其模糊子集为:{PZ，PS，PM，PB};Δkn的论域为:{-2，-1，-0.5，0，0.5，1，2}，其模糊子集为:{NB，NM，NS，ZO，PS，PM，PB};Δτn的论域为:{-0.01s，-0.006s，0.002s，0，0.002s，0.006s，0.01s}，其模糊子集为:{NB，NM，NS，ZO，PS，PM，PB}。考虑DSP的计算能力，各模糊子集的隶属度函数曲线选用形式简单、计算效率高的三角形和梯形形状。σ、ts、Δkn和Δτn的隶属度函数分别如图4中a、b、c和d所示。

图4 隶属度函数

2.2 模糊控制规则

模糊规则蕴含人工调整PI参数的经验，是整个参数模糊整定的核心。本文根据速度环增益和积分时间常数的作用及人工调整积累的经验制定模糊控制规则。制定规则的原则是:比例系数占主导作用，积分时间常数配合使用;优先按照减小调节时间方向调整。Δkn和Δτn的控制规则表如表1所示。

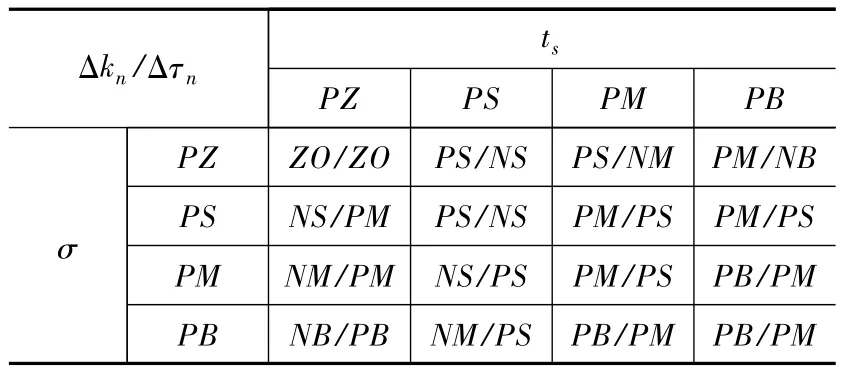
表1 模糊规则表

2.3 清晰化

由模糊推理得到的是一个模糊集合，不能直接用来调整PI控制器的参数，必须经过清晰化处理得到一个精确的量。清晰化的方法很多，这里采用工业控制中广范使用的加权平均法，其计算公式为:

其中，ki由规则的前件和输入的模糊集按一定的法则确定的值，ui为后件代表值，u*为计算输出的清晰值，n为规则数。

3 实验研究

实验装置为一电动机-发电机组，采用实验室自主研发，以TI公司DSP2812芯片为控制核心的交流伺服系统。电动机采用三洋P6系列PMSM电机，电机的基本参数如表2所示。

表2 电机基本参数

3.1 电流环对象辨识

如1.1节所述，取电流滤波时间常数为0，给定vq，得到iq的响应曲线如图5所示。

图5 vq-iq响应曲线

3.2 电流跟随实验

根据电机电流环对象参数，按照式(1)和(2)设计电流控制器参数。设定速度指令为nref=750sin(2πt)时的电流跟随实验波形如图6所示。

根据一阶惯性对象阶跃响应与参数之间的关系得到:

图6 电流跟随响应曲线

由图6可以看出，电流反馈虽然干扰较大，有些毛刺，但是能够紧紧跟随电流指令，满足设计电流环时对电流环跟随性的要求。

3.3 转速响应实验

速度阶跃响应如图7所示。图7a设定电机转速为750r/min，其中曲线a、b、c对应的PI参数分别采用模糊整定、人工整定、工程设计方法。实验中取调节时间为速度响应最后一次进入2%误差带的时间。表3为三条响应曲线对应的超调量和调节时间。图7b为采用模糊整定参数，速度指令分别为150r/min、300r/min、750r/min、1050r/min、1350r/min 时的响应曲线。

图7 速度阶跃响应

表3 速度阶跃响应性能

由图7及表3三种不同整定方法得到的响应可以看出，通过工程设计方法得到的响应曲线超调量很大，调节时间较长，不能满足对速度响应快速、准确的要求;人工整定曲线在超调量和调节时间指标上都明显优于另外两种整定方法，达到了较为理想的性能;模糊整定方法经过6次整定得到的响应已经接近人工整定的响应曲线，基本满足要求。在图7b中，在全速范围内选取不同速度设定值，阶跃响应均取得了较好的性能，控制器采用模糊整定后参数可在全速范围内运行。综上所述，经过速度控制器参数的模糊整定，速度响应得到了较大改善，在全速范围内运行平稳，取得了较好的控制效果。

4 结束语

本文对PMSM控制器参数的整定进行了研究。首先根据对象辨识及电机参数以工程设计方法设计控制器参数，然后设计速度控制器参数模糊整定。根据速度阶跃响应的超调量和调节时间，经模糊推理，离线调整控制器参数。实验表明，经过工程设计和较少次数离线调整，得到了较好的速度响应性能。本文应用所述方法，实现了数控加工中心进给轴驱动控制器参数的快速整定，增强了伺服系统适应性，适用于机床新安装或电机、负载发生变化后，首次运行前对控制器参数进行整定。

［1］Yoon-Seok H，Jung-Soo Choi，Sensorless PMSM driver with a sliding mode control based adaptive speed and stator resistance estimator［J］.IEEE Transaction on Magnetic，2000，36(5):3588-3591.

［2］陈荣，严仰光.永磁同步电机速度阶跃响应研究［J］.中小型电机，2005，32(1):41-451.

［3］Ziegler J G，Nichols N B.Optimum settings for automatie controllers［J］.Tran.A SME，1942，64:759-768.

［4］陶永华，尹怡欣，葛芦生.新型PID控制及其应用［M］.北京:机械工业出版社，1998.

［5］施伟锋，陈子顺，汤天浩.船舶发电机励磁系统的CMAC神经网络并行控制［J］.电网技术，2005，4(29):31-35.

［6］刘金锟.智能控制［M］.北京:电子工业出版社，2005.

［7］陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，2003.

Research on Controller Parameters Self-tuning of PMSM

NIU Yong-ling， PI You-guo
(College of Automation Science and Engineering，South China University of Technology，Guangzhou 510640，China)

This paper researches on controller parameters self-tuning of the double closed loop control system of Permanent Magnet Synchronous Motor(PMSM).The controller parameters of current loop are tuned by means of the engineering design method according to the parameters obtained by the identification of current loop’s object.The controller parameters of speed loop are tuned by means of fuzzy selftuning.According to overshoot and settling time of the speed response，the speed controller parameters are changed after getting the adjustment quantity by fuzzying，fuzzy reasoning and defuzzification and fixed until meeting the performance index.The experiment shows that this method improves the speed response and the controller parameters are tuned rapidly after the PMSM being fixed.

PMSM;engineering design method;fuzzy self-tuning;PID controller

TH16;TG65

A

1001-2265(2012)02-0084-04

2011-07-13

广东省产学研结合项目(2009B090300269)

牛永岭(1987—)，男，河南人，华南理工大学研究生，研究方向PMSM控制器参数自整定，(Email)scut_niuyl@139.com。

(编辑 赵蓉)