细长轴车削加工径向变形和切削力的分析计算

李 健，庞 勇

(广西工学院机械工程系，广西柳州 545006)

细长轴车削加工径向变形和切削力的分析计算

李 健，庞 勇

(广西工学院机械工程系，广西柳州 545006)

为减少细长轴的车削加工误差，论文对某细长轴的精加工车削和粗加工车削过程进行了分析，结合实际加工情况运用有限差分法和有限元法(不考虑加工机床主轴组件和尾座的刚性和考虑加工机床的刚性)分别求出精加工车削和粗加工车削过程细长轴外轮廓变形和径向切削力的变化，为细长轴的自动加工控制、减少加工误差提供各种数据，从而提高细长轴的加工质量。

径向变形;切削力;车削;细长轴

0 引言

细长轴车削加工国内外进行了不少的研究，国外主要集中于机理研究，国外学者Phan和Cloutier建立了车削加工中具有封闭解的工件变形的有限元模型［1］。国内研究主要在于细长轴车削加工理论误差分析和数控补偿加工的动态数值模拟［2-3］。本文主要研究应用有限差分法和有限元法(无刚度约束和有刚度约束)逐点求出精加工和粗加工细长轴车削过程中外轮廓变形和径向切削力的变化，为细长轴的装夹、自动化加工控制提供各种数据，以提高细长轴的加工质量。

1 有限差分法求轴的变形和切削力的变化

1.1 建立精、粗加工有限差分模型

本次研究选用直径为40mm，长度为1200mm的细长轴，采用CK6140为加工机床。初设粗、精加工的背吃刀量ap为2.5mm和0.2mm，其径向切削力计算公式如下:

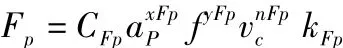
式中:Fp——径向切削力;

CFp——取决于工件材料和切削条件的系数;

xFp、yFp、nFp——背吃刀量 ap、进给量 f和切削速度vc的指数;

KFp——修正系数的积。

根据加工条件，查出各系数和指数值为:

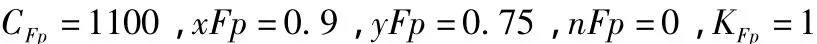
由于径向切削力的计算随背吃刀量ap的变化而变化，因此沿轴向方向把轴平均分成50段，每段长度均为h=0.024m。根据细长轴尺寸计算出各个截面相应的抗弯刚度 EI，计算与1、2、3、…、49 相对应截面上的弯矩Mi和相应的h2Mi/EIi。

根据差分法，把二阶导数差分公式代入挠曲线近似微分方程式，得:

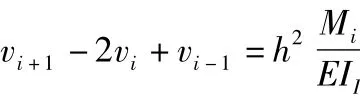
式中:Mi——梁在x=xi处的弯矩;

EIi——梁在x=xi处的抗弯刚度;

h——为各相邻点间的距离;

vi-1、vi、vi+1——为点的纵坐标。

根据上式对1、2、3、…、49各点列出差分方程，并注意v0=v50=0，得到49个方程，解49个子方程所组成的方程组即可得到各位置的挠度 v1、v2、v3、…、v49。

1.2 计算轴向各位置挠度和切削力

由于在车削过程中受径向车削力的影响，轴产生弯曲，导致背吃刀量变化，进而导致径向车削力变化，故需对模型进行49次求解。假设在截面i处的背吃刀量为D。即可求出径向车削力和作用在截面i处时的挠曲线，各位置的挠度为 v1、v2、v3、…、v49。取D-vi-1作为车削位置处于截面i-1时的背吃刀量，依次计算便可得出整个车削过程径向切削力和该力作用时的挠曲线。为了快速方便地计算出v1、v2、v3、…、v49，根据MATLAB软件的语言要求，对上面计算v1、v2、v3、…、v49的公式进行 MATLAB 程序编制，编程采用49×49矩阵，计算出轴粗加工过程的外轮廓径向位移结果(单位:mm)，将 v1、v2、v3、…、v49代替径向切削力公式F=1100*((0.5-d)^0.9)*(0.2^0.75)*1*1中的d，便可求得整个车削过程的径向切削力(单位:N):F0、F1、F2、…、F50，利用 MATLAB软件绘制精加工过程外轮廓径向位移变化曲线和径向切削力变化曲线，如图1、2所示。

同理可计算细长轴粗加工过程外轮廓径向位移的结果。利用MATLAB软件可绘制粗加工过程外轮廓径向位移变化曲线和径向切削力变化曲线，其结果如图3、4所示。

2 有限元法求细长轴的变形和切削力的变化

用有限元法求细长轴的变形时，分两种情况，一种是轴两端无刚度约束(即不考虑加工机床主轴组件和尾座的刚性)，另一种是轴两端有刚度约束(即考虑加工机床的刚性)。

2.1 轴两端无刚度约束时细长轴的加工变化

构建加工细长轴的有限元模型时，如果建立成三维实体，那么约束位置就必须分割面，且之后建立弹簧单元不方便，所以，选择在有限元软件中建立面单元，再旋转得到实体单元模型的方法建立有限元模型［4］。因为是逆向加工，而且要求出49个截面的变形和切削力，故从后面开始加力分析，为了与有限差分法对应分析，且轴向方向有100个单元格，故从右端开始每隔两个节点加力分析。施加载荷时从倒数第二个节点开始施加，从而可以求得切削力在倒数第二节点时整根轴的变形。因为需要求的是整个车削过程的外轮廓变形，故需求出下一节点的径向位移。例如:当径向切削力作用在倒数第二个节点时，需要知道的是下个节点(倒数第三个)的径向位移(位移方向与施加力方向平行)，进而可求得施加在该节点的径向切削力的大小，进一步可求得下一节点的径向位移。重复进行上述操作，便可求得整个车削过程的外轮廓变形和切削力的变化。利用MATLAB软件绘制有限元法对应的精、粗加工过程外轮廓径向位移变化和切削力变化曲线［5-6］，如图1、2、3、4(无刚度约束)所示。

图1 精加工过程外轮廓变形曲线对比

图2 精加工过程切削力变化曲线对比

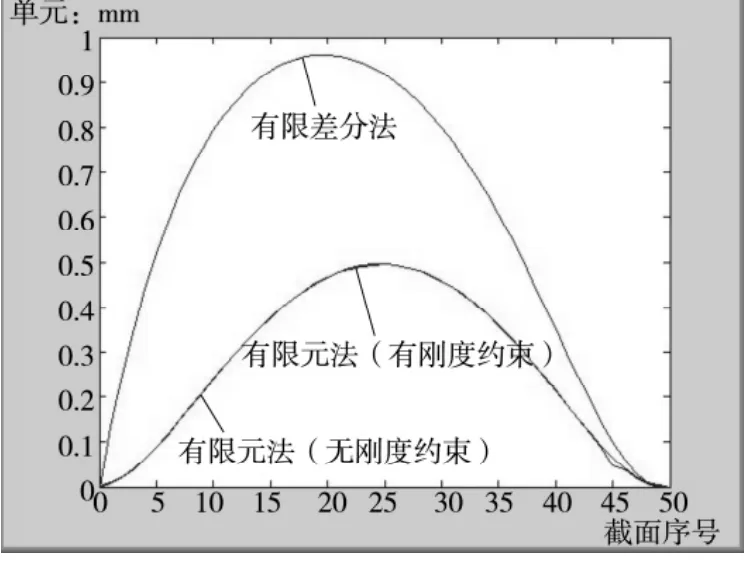
图3 粗加工过程外轮廓变形曲线对比

图4 粗加工过程切削力变化曲线对比

2.2 轴两端有刚度约束时细长轴的加工变化

首先求出加工细长轴机床CK6140数控车床的卡盘位置和尾座顶尖位置的径向刚度，根据加工机床主轴组件和尾座结构求得卡盘位置径向刚度K卡=1.85×105N/mm，尾座顶尖位置径向刚度K顶=1.44×105N/mm。在轴两端添加刚度约束的具体操作如下:

在细长轴的两个端面分别画4条长度均为10mm的线，线的一个端点为端面圆象限位置的关键点，然后添加弹簧单元和弹簧单元实常数，采用弹簧单元COMBIN14对所画的8条线进行网格划分并合并模型节点。

求解过程与无刚度约束时细长轴加工变化一样，求出整个车削过程各截面的外轮廓变形和切削力的变化，其结果如图1、2、3、4(有刚度约束)所示。

3 三种结果的对比分析

编写三种情况下精加工过程外轮廓径向位移和径向切削力变化的MATLAB程序，并绘制三种情况下精加工过程外轮廓径向位移和径向切削力变化曲线(如图1、2 所示)。

编写三种情况下粗加工过程外轮廓径向位移和径向切削力变化的MATLAB程序，并绘制三种情况下粗加工过程外轮廓径向位移和径向切削力变化曲线(如图3、4 所示)。

从图上的径向位移和切削力变化可看出，有限元法(无刚度约束和有刚度约束)计算结果相差较小，比较接近实际情况。

4 结束语

根据加工细长轴机床CK6140数控车床的特点，采用三种方法(有限差分法、无刚度约束有限元法、有刚度约束的有限元法)计算出精加工和粗加工细长轴车削过程中外轮廓变形和径向切削力的变化，为以后自动化车削加工提高加工质量提供了依据。

［1］A.-V.PHAN，G.CLOUTIER，J.R.R.MAYER.A ®Fnite lement model with closed-form solutions to workpiece dections in turning［J］.int.j.prod.res.1999，37(17):56-59.

［2］李玉玲，李志峰，为伟锋.车削加工细长轴的理论误差分析［J］.煤矿机械，29(10):22-25.

［3］胡韦华，王秋成.细长轴数控补偿加工的动态数值模拟［J］. 现代制造工程，2006(5):90-93.

［4］张洪信，赵清海.ANSYS有限元分析完全自学手册［M］.北京:机械工业出版社，2008.

［5］徐金明.MATLAB实用教程［M］.北京:清华大学出版社，北京交通大学出版社，2005.

［6］罗建军.MATLAB教程.电子工业出版社，2005.

Analysis and Calculating of Radial Distortion and Cutting Force in Long Shaft Turning

LI Jian，PANG Yong
(Mechanical Engineering Department，Guangxi University of Technology，Liuzhou Guangxi 545006，China)

To reduce the long shaft machining error，in this paper，the finish turning and the rough turning process are analyzed.We calculated the change of long shaft contour deformation and cutting force in the process of the finish turning and rough turning with limited difference method and the finite element method(without regard to machine tool rigidity and rigidity in both ends).The data is offered for turning control to improve the processing quality of long shaft.

radial distortion;cutting force;turning;long shaft

TH135

A

1001-2265(2012)02-0023-03

2011-07-19;

2011-08-18

李健(1965—)，男，广西人，广西工学院机械工程系教授，主要研究方向为数字化设计与制造，(E-mail)gxlzlj@tom.com。

(编辑 赵蓉)