基于模糊积分分类器的一种改进

王 强，马生全

（1.三亚学院 理 工学院，海南 三亚 572022；2.海南师范大学 信息科学与技术学院，海南 海口 571158）

基于模糊积分分类器的一种改进

王 强1，马生全2

（1.三亚学院 理 工学院，海南 三亚 572022；2.海南师范大学 信息科学与技术学院，海南 海口 571158）

通过对传统积分分类器的改进，引入正向和负向两个隶属评价来进行最终的评价，利用复值函数的模糊积分给出示例最终的隶属评价，让复值函数的积分在分类技术中得到了应用，丰富了模糊积分在分类技术中的应用形式，给出了在进行最终隶属评价的三种处理方式.

模糊积分；分类器；隶属评价；乐观因子；模糊推理

分类问题是模式识别系统的重要组成部分，分类是根据已有的示例学习分类器，然后将新数据利用该分类器分为符合实际情况的不同类别，常见的分类方法有贝叶斯推理、神经网络、线性方法、最邻近等等.随着模糊集合理论的发展也带来了新的分类器，比如基于模糊积分的分类器.模糊积分是一种基于测度的积分[1]，其在综合评判中的应用已经很广泛，克服了传统的加权平均带来的不符合逻辑的弊端.王熙照等人将模糊积分运用于分类技术中，也得到了很广泛的应用[2].

1 模糊积分分类器介绍

模糊积分的分类可以表示如下[2]：

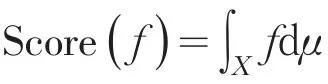
则初等模糊积分分类器

如下定义：如果

这样定义的模糊积分分类器是一个经典的分类器，其输出是一个布尔向量.

定义2 设有一个c类的分类问题，X={x1，x2，…，xn}表示属性集，f=（f（x1），f（x2），…，f（xn））为定义在X上的实值函数，令，这里μi为第i类所对应的模糊测度，则

这种积分分类器的输出是一个[0，1]区间上c维向量.这样给出的输出实际上是该示例在每一类上的隶属评价，这样根据最大隶属原则便能得到该示例的最终类别.

2 模糊积分分类器的改进

上述定义2的积分分类器与定义1的积分分类器的区别在于初等积分分类器只采用了一组模糊测度，而定义2的积分分类器则分别在每一类上都给出了一组模糊测度，然后分别在每一类上进行模糊积分，其输出应该是在每一类上的隶属评价.最后根据最大隶属原则来得到最终的分类类别.值得注意的是，对某一示例，属性值f（xi）代表的是第i个属性对最终类别的支持度，所以定义2定义是一种正向的评价.本文的一种改进的思想是利用正向和负向两个方面的综合评价来进行最终的分类.

定义3 设有一个c类的分类问题，X={x1，x2，…，xn}表示属性集，f=（f（x1），f（x2），…，f（xn））为定义在X上的实值函数，即在每一个属性上的正向评价，每一分量的值都是介于0与1之间，则1-f=（1-f（x1），1-f（x2），…，1-f（xn））为在每一个属性上的负向评价，令，这里 μi为第i类所对应的模糊测度，则这种积分分类器所得到的输出是一组二维向量

（ak，bk）代表的是该示例隶属于第k类的正向隶属评价和负向隶属评价度.令dk=ak-bk，k=1，2，…，c，则可以根据最大隶属度原则给出其最终的分类.

如果我们将一组二维向量看成一组复数向量，于是我们可以得到定义4：

定义4 设有一个c类的分类问题，X={x1，x2，…，xn}表示属性集，f=（f（x1），f（x2），…，f（xn））为定义在X上的实值函数，即在每一个属性上的正向评价，每一分量的值都是介于0与1之间，则积分分类器所得到的输出是一组复值向量

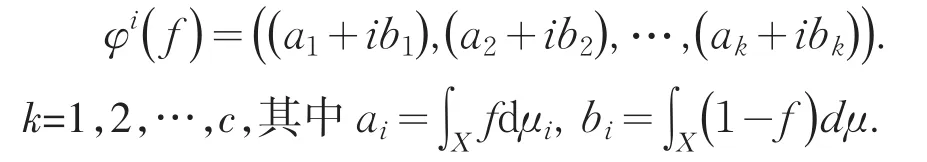
该定义也可以将属性的输出看成是一个复值函数，其中实部代表的是对该属性的正向评价，虚部代表的是对该属性的负向评价，然后利用复值函数的模糊积分可以得到示例分别对每一类的隶属评价，其值也是一个复数，实部代表了正向的隶属评价，虚部代表的是负向的隶属评价.通过传统积分分类器的改进，引入负向隶属评价，使得对分类的刻画更加全面.

3 实例计算

考虑表1所示的4个示例的两类问题：

表1 属性值Tab.1 Attribute Value

根据本文第二节，可以将其属性值看成是一个二维向量（或者是复数），于是得到表2所示的属性值表：

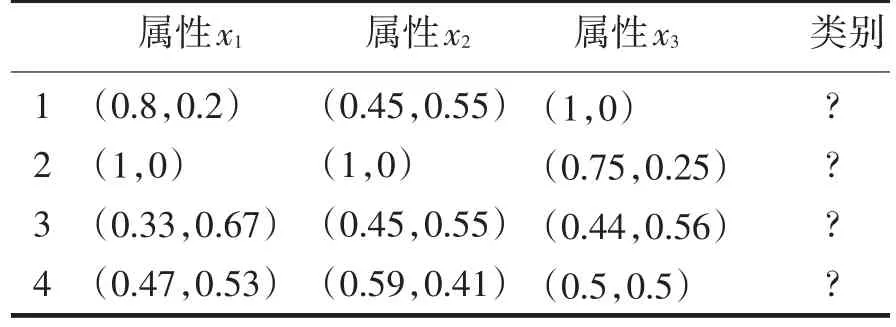
表2 改进后的属性值表Tab.2Improved Attribute Value

定义在每一类上的模糊测度（见表3）.

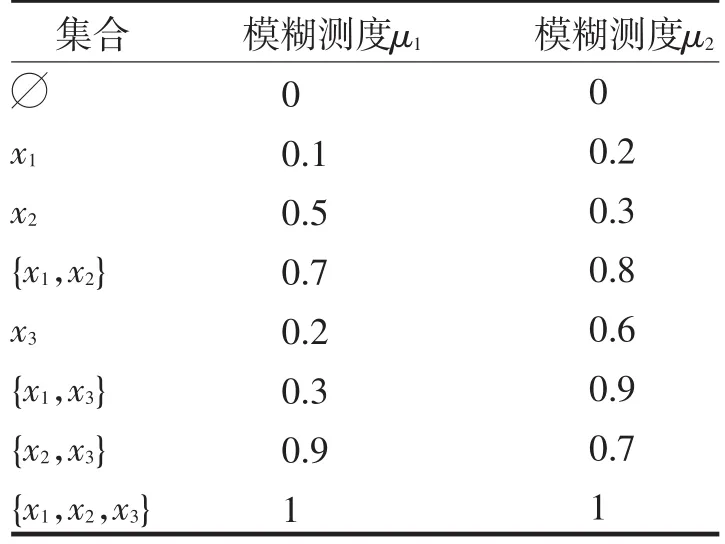
表3 模糊测度Tab.3 Fuzzy Measure

利用定义3给出的积分分类器进行分类，采用Choquet积分得到表4.

其最终的隶属程度的评价为下表5所示.

于是可以得到第一个示例其最终的分类为类2，第二个示例其最终的分类为类1，第三个示例其最终的分类为类1，第四个示例其最终的分类为类1.由于这种分类器是单从正向的评价，不足以去刻画某个示例隶属于哪一类，于是从正向和负向两个方向去刻画其在某一类上的评价值，从上述例子可以看到，如果仅从正向去评价其属于某一类的程度，示例2应该隶属于第2类，如果从正向和负向来考虑的话其应该是属于第一类的，这种积分分类器要求我们要综合考虑隶属评价值，符合人的逻辑.当然这种分类器也是基于模糊积分的分类器，模糊积分的选择以及模糊测度的给出都会给最终的分类带来很大的影响，因此要根据具体情况来选择具体的模糊积分.

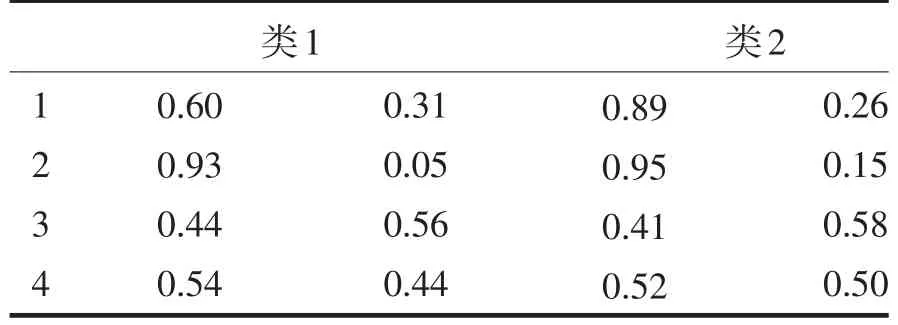
表4 Choquet积分的结果Tab.4 The Consequense Choquet Integrals

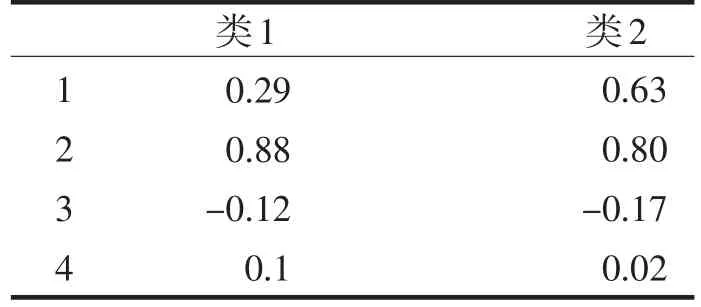
表5 最终隶属评价Tab.5The Final Membership Evaluation

4 最终隶属评价的两种处理方式

当然用dk=ak-bk来刻画最终的隶属评价值也会显得很粗糙，于是有以下两种方式来对上述方法再一次进行改进.

第一种方法，可以引进乐观-悲观因子[3]，即将dk表示成 ak与 bk的线性函数，令 dk=αak-（1-α）bk，选择不同的α会得到不同的分类结果.

另外一种方法是同模糊推理[4]的方式来进行最终的分类，其基本思想是由于最终的隶属评价是由正向和负向两个方面去刻画，并且认为某个示例隶属于某一类的正向评价越大，负向评价越小，则该示例隶属于这一类的程度就会越大.因此我们可以建立正向隶属评价，负向隶属评价与最终隶属评价的模糊规则库，对每一个示例利用模糊推理得到其最终的评价.具体步骤如下：

第一步 建立正向隶属评价与负向隶属评价的模糊集；

第二步 建立建立正向隶属评价，负向隶属评价与最终隶属评价的模糊规则库；

第三步 输入正向隶属评价，负向隶属评价值，利用Mattlab中模糊逻辑工具箱进行求解[5].

下面分别给出刻画正向隶属评价和刻画负向隶属评价的语言变量“高”“中”“低”的模糊集

正向隶属评价“高”，记为s型模糊数，pos.high＜0.5,1＞

正向隶属评价“中”，记为三角型模糊数，pos.mid＜0,0.5,1＞

正向隶属评价“低”，记为反s型模糊数，pos.low＜0,0.5＞

负向隶属评价“高”，记为s型模糊数，neg.high＜0.5,1＞

负向隶属评价“中”，记为三角型模糊数，neg.mid＜0,0.5,1＞

负向隶属评价“低”，记为反s型模糊数，neg.low＜0,0.5＞

接下来给出刻画综合隶属评价的语言变量“高”，“稍高”，“中”，“稍低”，“低”的模糊集.

综合隶属评价“高”，记为s型模糊数，com.high＜0.75,1＞

综合隶属评价“稍高”，记为三角型模糊数，com.lithigh＜0.5,0.75,1＞

综合隶属评价“中”，记为三角型模糊数，com.mid＜0.25,0.5,0.75＞

综合隶属评价“稍低”，记为三角型模糊数，com.litlow＜0,0.25,0.5＞

综合隶属评价“低”，记为反s型模糊数，com.low＜0,0.25＞

根据专家知识和经验可以给出如下几条双入单出的模糊推理规则：

1）如果正向隶属评价“高”，负向隶属隶属评价“低”，则综合评价“高”

2）如果正向隶属评价“高”，负向隶属隶属评价“高”，则综合评价“中”

3）如果正向隶属评价“高”，负向隶属隶属评价“中”，则综合评价“稍高”

4）如果正向隶属评价“中”，负向隶属隶属评价“低”，则综合评价“稍高”

5）如果正向隶属评价“中”，负向隶属隶属评价“中”，则综合评价“中”

6）如果正向隶属评价“中”，负向隶属隶属评价“高”，则综合评价“稍低”

7）如果正向隶属评价“低”，负向隶属隶属评价“低”，则综合评价“中”

8）如果正向隶属评价“低”，负向隶属隶属评价“中”，则综合评价“稍低”

9）如果正向隶属评价“低”，负向隶属隶属评价“高”，则综合评价“低”

有了这9条规则后，根据Mamdani的CRI算法，利用中心解模糊计算出其综合的隶属评价.表6给出了其属于各类的综合隶属评价：

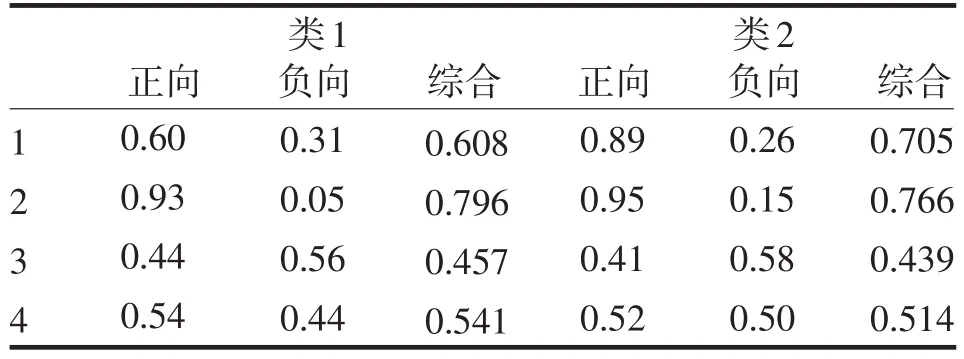
表6 利用模糊推理计算出的综合隶属评价Tab.6The Comprehensive Membership Evaluation Based On Fuzzy Inference

选择Mamdani蕴含算子，t-范数为取小，利用Mattlab计算得到每个方案的评价值，评价值越小即排名越高，经过计算得到四个示例的综合隶属评价.

根据改进的模糊推理进行最终隶属评价，得到上述四个案例分别是属于2、1、1、1类.

运用模糊积分工具，利用双向隶属评价和模糊推理方法来进行案例的最终分类，体现了分类的全面性和客观性，达到了较好的分类效果.

[1]Sugeno M.Theory of Fuzzy Integrals and Applications.[D].Tokyo Institute of Technology,1974.

[2]王煕照.模糊侧度和模糊积分及其在分类技术中的应用[M].北京:科学出版社,2008.

[3]徐玖平.多属性决策的理论与方法[M].北京:清华大学出版社,2007.

[4]闻新,周露,李东江.Matlab模糊逻辑工具箱的分析与应用[M].北京:科学出版社,2001.

[5]Zadeh L A.Fuzzy sets[J].Information and Control,1965(8):338-353.

责任编辑：毕和平

Improvement of Fuzzy Integral Classifier

WANG Qiang1，MA Shengquan2
（1.College of Technology，Sanya College，Sanya 572022，China；2.College of Information Science and Technology，Hainan Normal University，Haikou 571158，China）

Through the improvement of classifier of the traditional integration,by introducing positive and negative membership evaluations to make the final evaluation,we use fuzzy Integral of the complex-valued functions to give the sample final membership evaluation,put integration of complex-valued functions into use in classification technology,expand the way fuzzy integral performs in classification technology,and offer three ways to deal with the final member⁃ship evaluation.

Fuzzy Integral;classifier；Membership evaluation；positive factor；fuzzy reasoning

O 159

A

1674-4942（2012）03-0259-04

2012-06-05