简单二人零和博弈的一种图解法
2012-09-11马赞甫刘妍珺
马赞甫,刘妍珺
(1.贵州财经大学 经济研究所,贵州 贵阳 550004;2.贵州财经大学 数学与统计学院,贵州 贵阳 550004)
简单二人零和博弈的一种图解法
马赞甫1,刘妍珺2
(1.贵州财经大学 经济研究所,贵州 贵阳 550004;2.贵州财经大学 数学与统计学院,贵州 贵阳 550004)
利用等分量线及支付凸多边形这两个基本概念,以图解方式确定简单二人零和博弈(2×n或m×2)的纳什均衡.这一方法与通常的图解法是互补的,可率先确定持有多个纯策略的局中人的均衡策略.
二人零和博弈;图解;凸组合;等分量线
二人零和博弈是现实生活中常见的博弈形式,也是博弈论发展早期数学家特别感兴趣的一类博弈模型.事实上,与有限零和博弈相联系的最小最大值原理[1]在博弈论中占有极为重要的地位.
对于有限二人零和博弈混合战略纳什均衡的确定,一般是借助最小最大值原理,将之转换为一个线性规划问题,然后利用单纯形方法确定最优策略.而对于某局中人只有两个纯战略的简单的二人零和博弈,习惯上采用基于最小最大值原理的一般图解法.一般图解法简单直观,对于确定一个参与人的均衡战略极为便利,早期的博弈论著作都对这一方法有所提及[2-3].
一般图解法只能确定一个局中人的最优策略,确切地说,只能确定纯战略个数为2的局中人的最优策略,在此基础上再以代数方法确定另一参与人的均衡策略.我们提出另外一种基于凸组合的互补方法,可率先确定纯战略个数大于2的局中人的最优策略.另外,这一方法也可直接确定博弈的值.
1 二人零和博弈
考虑一个二人有限零和博弈模型.假设局中人1的纯策略有m个,局中人2的纯策略有n个,分别记局中人1、2的混合策略为
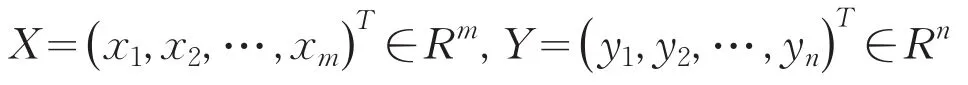
其中x1,…,xm,y1,…,yn≥0,分别满足.当局中人1选择第i个纯战略而局中人2选择第j个纯战略时,局中人1的支付为aij,局中人2的支付为(-aij),i=1,…,m,j=1,…,n.该博弈可由如下支付矩阵A给出:

称一个策略组合(X*,Y*)为纳什均衡(Nash Equilibrium,N.E.),当且仅当X*∈argmXax{XTAY*}与Y*∈argmYax{X*TAY} 同时成立,此时称v*=X*TAY*为博弈的值.
对于由A所给出的二人零和博弈,当m与n皆大于2的时候,确定均衡比较棘手,但对于两者最小值为2的情形,有简单的处理方法,即利用图解法确定最优策略.一般的对策论著作中都会介绍2×n或m×2型零和博弈的图解法,基本思路是利用最小最大值原理,描绘最小(或最大)值曲线,然后再求最小(或最大)值曲线的最高(或最低)点.我们称这种方法为一般图解法.
一般图解法能直接确定双战略拥有者的最优战略,但两个以上纯战略持有者的均衡战略是以间接方式给出的.我们提出另外一种互补方法,能直接确定多战略持有者的均衡战略,该方法的理论基础是最大等收益法则.
一般而言,若(X*,Y*)是纯战略均衡,则可根据最小最大值原理直接予以确定,若纳什均衡(X*,Y*)不是纯战略均衡,则需满足最大等收益法则.所谓最大等收益法则,即:如果

存在两个非零分量>0与>0,则当局中人2选择Y*时,局中人1的第i1、i2个纯战略所对应的期望支付必须都等于v*,且均不小于其它任意纯战略所带来的期望支付;类似地,若
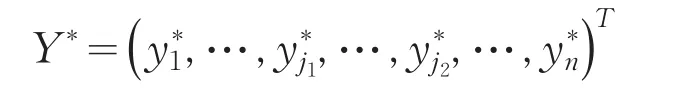
存在非零分量>0与>0,则当局中人1选择X*时,局中人2的第j1、j2个纯战略也对应等量的最大的期望支付(-v*).
利用最大等收益法则,可考虑一种凸组合图解方法:在支付凸组合的基础上,利用等分量线确定博弈的解与值.
2 凸组合图解法
考虑一个由2×n阶支付矩阵所定义的简单零和博弈.设该博弈的纳什均衡为(X*,Y*),所对应的博弈值为v*=X*TAY*.由于AY*是矩阵n个列向量的凸组合:

因此,当均衡战略X*=(x*,1-x*) 满足0<x*<1时,必有
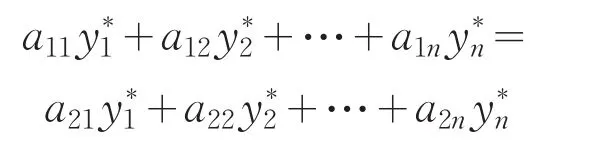
则v*与向量AY*的任一分量值相等.这表明,均衡状态对应凸组合图形中的一个向量,该向量的两个分量必须相等.
视支付矩阵A的每一列为二维坐标平面上的一个点,对这n个点做凸组合,得到一个凸多边形,另,定义等分量线v1=v2,则等分量线与凸多边形的位置关系无外乎相离与相交两种情况.
1)凸多边形位于等分量线同侧.如图1所示.在这种情况下,参与人1存在一个(弱)占优策略,博弈有一个重复剔除占优均衡.
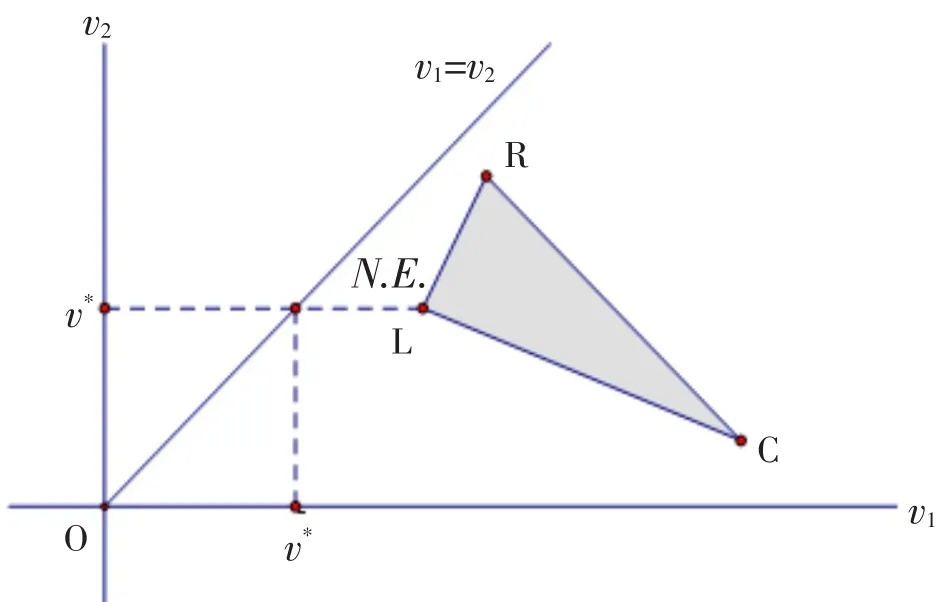
图1 等分量线与凸多边形相离Fig.1 The separation set of iso-component line and convex polygon
2)等分量线与凸多边形相交,在这种情况下存在混合战略均衡,且坐标最小的一个交点给出博弈值及均衡策略.不妨考虑一个2×3的零和博弈,其一般形式如表1所示:
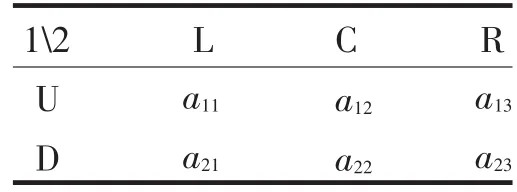
表1 2×3型零和博弈的一般形式Tab.1 The General Form of 2×3 Zero-Sum Game

可解得

另一方面,由于局中人2在均衡状态下以零概率选择纯战略R,因此有

就几何位置而言,若支付点(a13,a23)T位于点(a11,a21)T及点(a12,a22)T所连直线
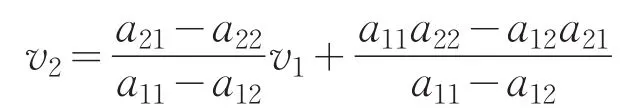
的上方①该线段必须是下降的,否则其上侧端点必对应于参与人2的劣战略,不可能出现于其混合战略之中.因此,其它支付点当位于该线段所在直线上方.为防止出现意外情况,画图前最好先剔除劣战略.,则必有

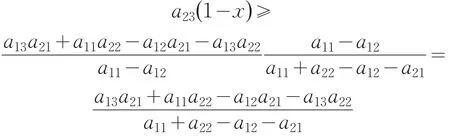
则局中人2选择纯战略R对应的负支付满足
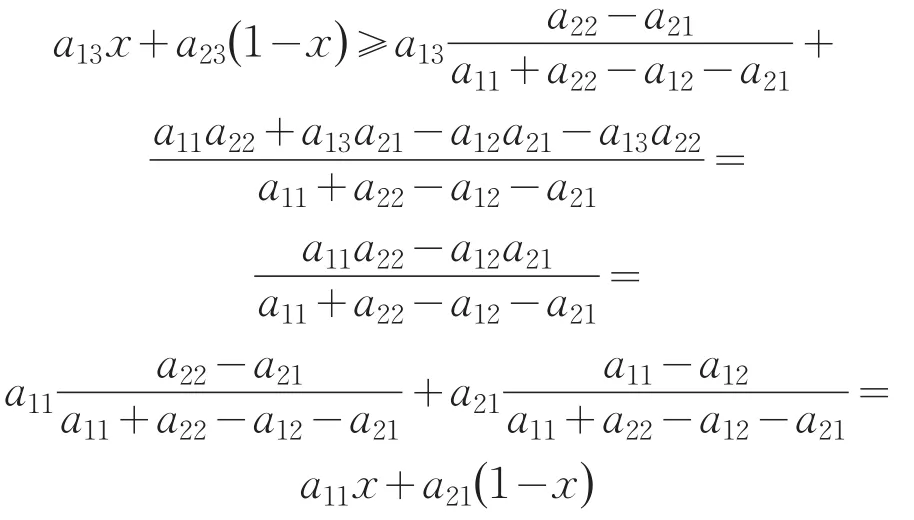
或者说,给定局中人1的均衡战略(x,1-x)T,相较纯战略R而言,局中人2选择纯战略L或C将带来更高的期望收益.如图2所示,三角形的顶点L、C、R分别由支付矩阵的列向量1、2、3所确定,由于R点位于直线LC的上侧,这一几何位置关系使得均衡状态下的局中人2必须以零概率选择纯战略R.
进一步可证明,根据直线LC与等分量线交点N.E.的几何位置可确定博弈值及均衡战略组合.显然,N.E.点可表示为三角形顶点L、C、R的一个凸组合,或者说,N.E.点坐标(e11,e21)T满足如下条件:
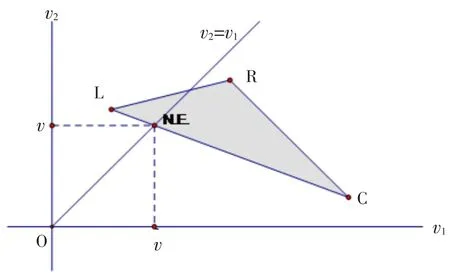
图2 等分量线与凸多边形相交Fig.2 The intersection of iso-component line and convex polygon
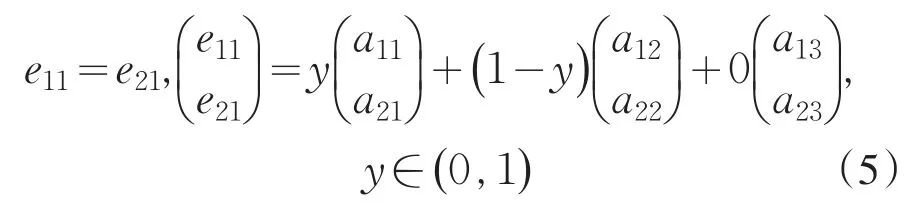
无疑,均衡未必单一,甚至存在无穷多均衡的情况.比如,当支付列向量存在至少三点共线时,可能出现无穷多均衡.如图3所示,支付点L、C、R共线,等分量线与直线LCR的交点N.E.存在无穷多的凸组合形式,此时有无穷多均衡.
以上考虑的是2×n型零和博弈的图解法,相仿佛的,对于m×2型零和博弈,可先确定参与人1的均衡战略.方法是视支付矩阵A的每一行为二维坐标平面上的一个点,对其进行凸组合得到一个凸多边形,考虑等分量线与该凸多边形坐标最大的一个交点,该交点确定了博弈的均衡.

图3 无穷多均衡Fig.3 The infinite Nash Equilibrium
3 示例及结语
考虑一个2×n型的零和博弈.设参与人1有两个纯战略:U、D,参与人2有三个纯战略:L、C、R;给定纯战略组合,参与人1的支付见表2.

表2 一个2×n型零和博弈Tab.2A 2×n Zero-Sum Game
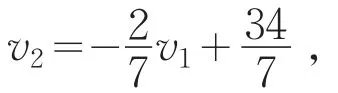
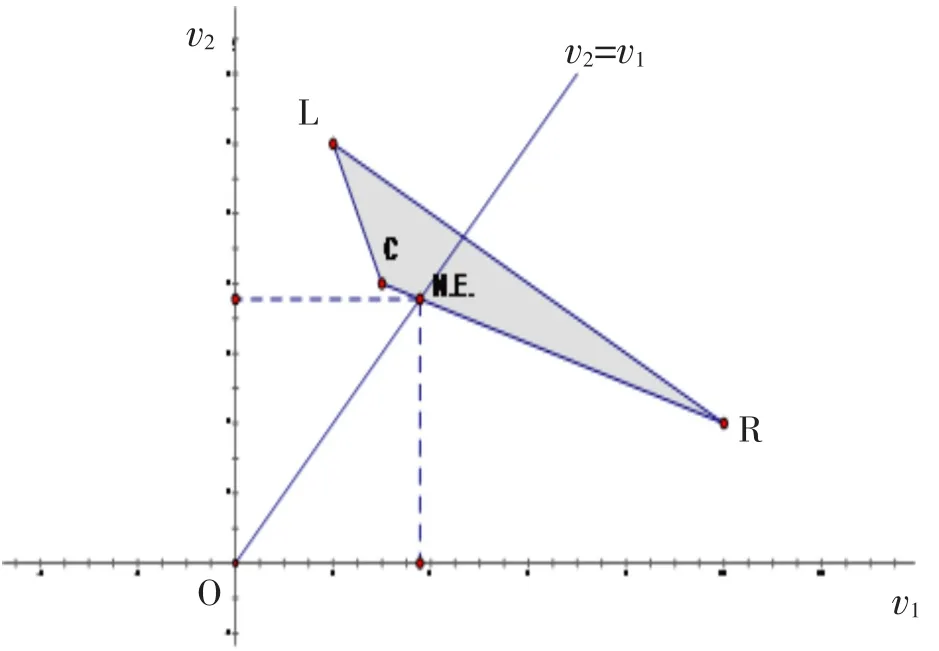
图4 2×n型零和博弈求解示意Fig.4The schematicdiagram for the 2×n zero-sum game
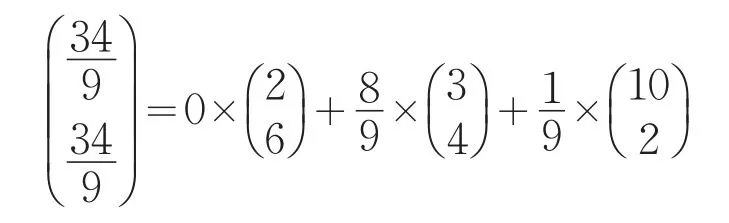

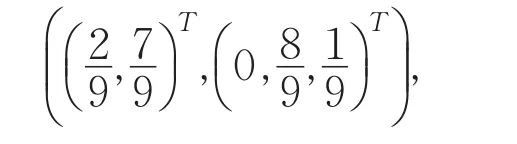
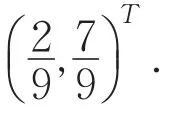
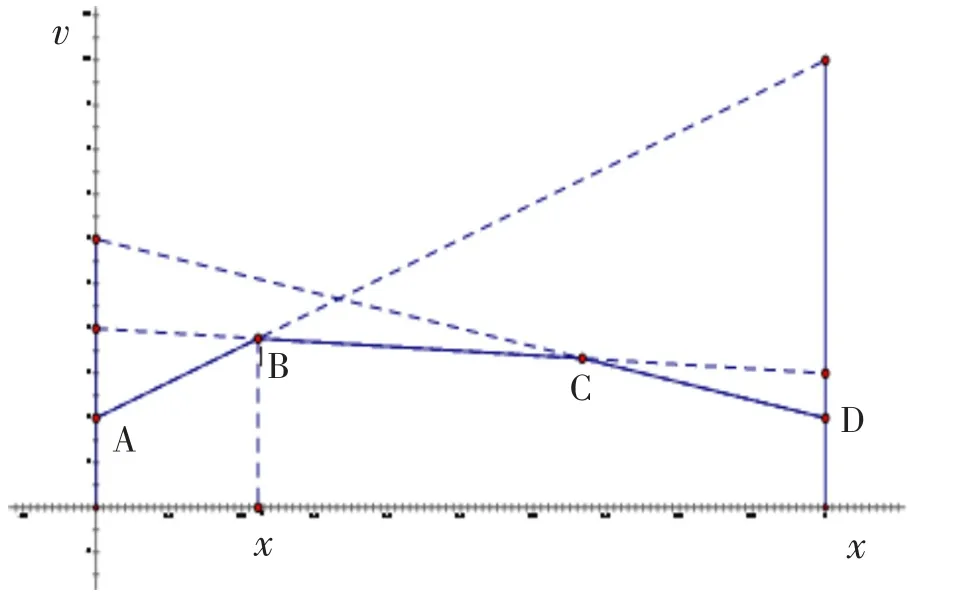
图5 一般图解法示意Fig.5The General graphic method diagram for the zero-sum game
再考虑一个m×2型的零和博弈.设参与人1有三个纯战略:U、M、D,参与人2有两个纯战略:L、R;给定纯战略组合,参与人1的支付如表3所示.
本例中需要先确定局中人1的均衡策略,如前所述,均衡由等分量线与凸多边形坐标最大的交点所决定.在图6中,UM所在直线方程为17,与等分量线的交点为N.E.,博弈均衡由N.E.点给出,由于
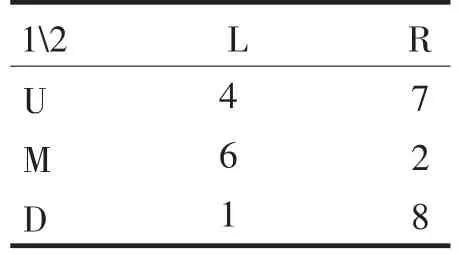
表3 一个m×2型零和博弈Tab.3A m×2 Zero-Sum Game
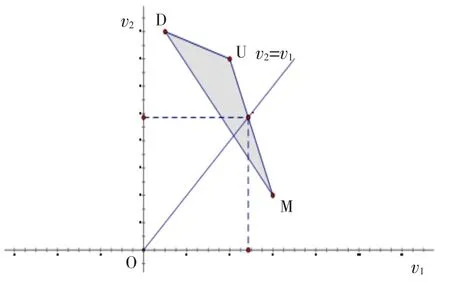
图6 m×2型零和博弈求解示意Fig.6The schematic diagram for the m×2 zero-sum game

总之,与一般图解法一样,凸组合方法可以确定简单零和博弈的纳什均衡及均衡的值,不同点在于凸组合方法首先确定的是多个纯策略拥有者的混合策略,而一般图解法确定的是仅拥有2个纯策略的局中人的混合策略.因此,凸组合方法可说是一般图解法的互补方法.
[1]John von Neumann.Zur Theorie der Gesellschaftsspiele[J].Mathematische Annalen,1928(100):295-300.
[2]J·麦克金赛.博弈论导引[M].北京:人民教育出版社,1960.
[3]王建华.对策论[M].北京:清华大学出版社,1986.
责任编辑:毕和平
A Graphic Method for the Simple Two-Person Zero-Sum Games
MA Zanfu1,LIU Yanjun2
(1.Institute of Economic Research,Guizhou University of Finance and Economics,Guiyang 550004,China;2.School of Mathematics and Statistics,Guizhou University of Finance and Economics,Guiyang 550004,China)
By the introduction of iso-component line and convex polygon,a graphic method was presented to solve sim⁃ple zero-sum two-person games.This approach,which is complementary to the general graphic method,can determine the Nash equilibrium strategy of the player who holds more pure strategies.
two-person zero-sum game;graphic method;convex combination;iso-component line
F 224.32
A
1674-4942(2012)03-0249-05
2012-02-27
教育部人文社科基金项目(12YJC790140)
