基于支持向量机的新经济增长点选择研究

张 倩

基于支持向量机的新经济增长点选择研究

张 倩

（西安财经学院统计学院，陕西西安710100）

针对现阶段新经济增长点选择模型无法区分“已有的”增长点与“新的”增长点的问题，使用支持向量机挖掘新经济增长点的潜在性。研究显示：陕西省2010年38个工业行业可划分为“新经济增长点”与“非新经济增长点”两类，新经济增长点一类中前十位行业与陕西省“十二五”规划中的文化产业、高新技术产业、新能源产业发展相一致，可见支持向量机在新经济增长点选择中的可行性和可靠性。

新经济增长点；支持向量机；产业

一、引 言

2008年，中国政府为应对由美国次贷危机引起的全球性金融危机，通过投资四万亿元拉动经济增长，使得中国的经济增长模式由出口型向内需型转变，虽然在一定程度上有效地缓解了金融危机带来的影响，但其不可持续性已成定论。“十二五”期间寻找新的经济发展契机、培育新经济增长点已成为各级政府统筹经济工作的重点。如何能够找到新的增长点，将选择过程变得有根有据，为政策制定提供依据，是本文研究的出发点。

经济增长点理论来源于经济不平衡增长理论，法国经济学家弗朗索瓦·佩鲁（F．Perroux）在《经济空间：理论的应用》和《略论发展极的概念》等著述中最早提出了“发展极”（Poles of Development）理论，他认为某些主导产业或有创新能力的企业在一些区域的聚集和优先发展形成经济活动中心，这些中心具有辐射作用，可以带动一个地区的经济发展［1］。在西方，新经济增长点主要指的是地理上的经济活动中心，在我国，新经济增长点主要指产业上的带动作用［2］。由此可见，新经济增长点是一个经济属性与空间属性并重的概念，是经济点与空间点的结合［3］。本文认为，新经济增长点是一切能引起经济增长的潜在因素，不仅具有经济属性和空间属性，同时也具有时间上的潜在性，即不是已有的、成熟的增长点，而是在现阶段尚不明显或已初现，但在不久将来，因其巨大的成长性和带动作用将成为一个时期发展的主流。新经济增长点的选择模型主要有三种：选择图谱法［4］，线性模型法［3］，因子分析法［5］。现有方法存在两点不足，第一，没有突出新经济增长点的潜在性，区分出“已有的”增长点与“新的”增长点；第二，没有指明新经济增长点具体的增长环节。

支持向量机（Support Vector Machine，SVM）方法是建立在统计学习理论和Vapnik－Chervonenkis（VC）维概念的基础之上［6］225－260。虽然统计学习理论论证坚实，理论完善，但是它对所研究对象的样本数目要求较高，往往要有趋于无穷大的渐近行为，而实际问题中，研究对象的样本数目有限，通常很难满足以上假设前提。支持向量机的出现，为解决有限样本学习问题提供了有力支持。郑治伟、孟卫东使用支持向量机对重庆市主导产业进行了预测［7］，研究结果同“十一五”期间重庆市产业现状和未来产业规划基本吻合，证实了支持向量机的科学性、合理性和前瞻性。

前人的研究成果启发了笔者的研究思路。SVM是一种典型的两类问题分类器，可以根据已学会的知识和处理问题的经验对复杂问题做出合理的判断决策，给出较满意的解答［8］。对于新经济增长点的选择问题，可以使用过去的“新经济增长点”对模型进行训练，识别出未来的“新经济增长点”的时间属性。同时，针对新经济增长点选择更为具体、微观的特点，在选择出新经济增长点后，将行业与本地区的自然资源和行业发展动态相结合，寻找具体的增长环节，完成新经济增长点的微观化，加深对增长环节具体化的理解和研究。

二、计量模型及测量指标

（一）支持向量机简介

支持向量机是由V．Vapnik和A．Lerner提出的一种新型的基于统计学习理论的机器学习算法。自从20世纪90年代提出相关概念后，SVM已在手写体识别、图像分类、时间序列预测等领域取得了广泛的应用和丰硕的成果。随着对支持向量机的不断深入研究，它已经成为机器学习和数据挖掘最重要的工具之一。

SVM模型主要应用于样本点的分类问题。在线性可分的情况下，如图1所示，对于分别属于H1和H2的两类样本点，可以轻易地找出一条直线H，将两类样本很好地区分开来。在无法用直线来分类样本点的情况下，SVM通过寻找唯一的分类间隔最大超平面来解决分类问题。在图1中，超平面H1由两个空心圆张成，超平面H2由两个实心圆张成。这四个样本称为支持向量。所谓分类间隔最大超平面就是指平行H1和H2的超平面H，它不仅能将H1和H2正确分类，而且使得两者之间的距离最大。

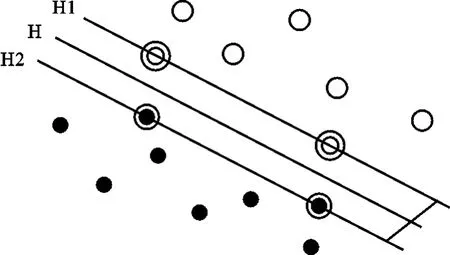
图1 线性可分情况下的最优分类面

超平面H的方程为x·w＋b＝0，在对其进行归一化之后，线性可分的样本集（xi，yi），i＝1，…，n，x∈Rd，y∈｛＋1，－1｝，满足：

此时分类间隔等于2／｜｜w｜｜。寻找最优超平面等价于在约束条件（1）下，使最小。以上优化问题等价于下述对偶问题：

其中αi为Lagrange乘子。该二次函数优化问题存在唯一解。解中非零αi所对应的样本就是支持向量，相应的最优分类函数是：

b＊是最优超平面的偏移量，通常由分类后的支持向量求均值所得。

无论是直线还是超平面，在线性可分的情形下，总可以在原空间上利用SVM解决分类问题。但是对于线性不可分的情况，在原空间上已不能直接应用上述分类手段，必须利用非线性特征函数Φ∶Rd→W，将原空间上线性不可分的情形转换为特征空间上线性可分的情形，才能够继续利用SVM进行分类。由于无法直接在高维的特征空间上利用特征函数计算分类超平面，为此，引入核函数K（x，y）的概念。核函数，就是原空间上的非线性映射，它的函数表现为特征函数的点积形式，即K（x，y）＝Φ（x）· Φ（y）。因此，特征空间上的分类问题可以转化为支持向量在核函数上的权重和问题。此时，分类函数的形式为：

常用的核函数有以下三种：

1．多项式核函数

K（x，y）＝［（x·y）＋1］d

2．径向基核函数

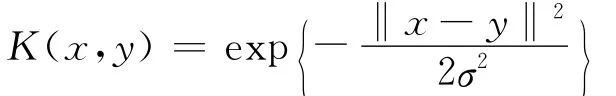
3．Sigmoind核函数

K（x，y）＝tanh（k（x·y）＋c）

实际应用中，由于径向基函数实现非线性映射时使用参数较少，往往成为选择核函数时的首选。本文即选用径向基函数作为核函数进行SVM分类。

从以上介绍可知，相对其他统计方法，SVM具有以下优势：

1．在有限样本的前提下，可以求出问题的最优解，降低了收集样本信息的成本；

2．SVM模型得到的结论是全局最优的，克服了其他方法中无法避免的局部极值问题；

3．通过引入核函数，使得可以仅仅通过两个原始低维空间中的向量，获得高维特征空间中的向量内积，解决了在高维空间中难以求解最优超平面的难题。

（二）建立分类模型

1．训练样本数据预处理

（1）对训练样本归一化，消除量纲的影响；

（2）yqi采用如下策略进行调整：若行业属于新经济增长点，则yqi＝1；反之，yqi＝－1。

2．建立SVM模型分类器

取径向基函数为核函数，利用训练样本（xi，yi）求解如式（5）的二次优化问题，从而获得（αi，b）及其对应的支持向量：

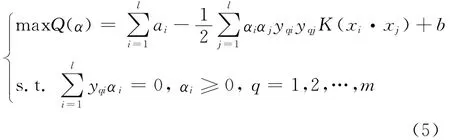
利用获得的αi，b和支持向量，得到行业的分类模型：

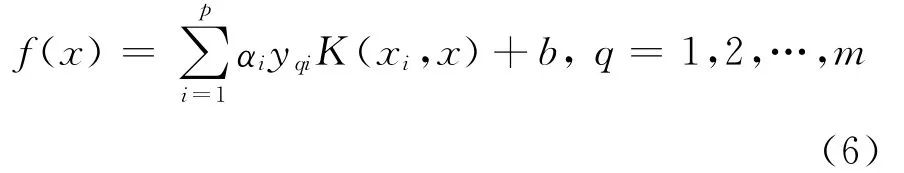
重复上述分类过程l次，得到l个行业分类模型。

3．判别行业是否属于新经济增长点

利用获得的判别模型，即可根据行业输入模式，判别行业是否属于新经济增长点。若第q个行业的输出等于1，则该行业属于新经济增长点；若输出为－1，则该行业不属于新经济增长点。

（三）指标体系的设立

新经济增长点是指那些处于潜在状态，尚不明显或者已初现，具有良好的发展势头和前景，能在不久的将来发挥作用的经济增长点，结合经济增长点的特征，经济增长点的选择应依据以下三点原则：

1．增长潜力与成长性。新经济增长点要有发展潜力和成长性，对经济增长贡献要大，能够成为拉动经济增长的主导力量。同时，具有技术进步带动作用，技术进步才能使得增长点由外延式增长转变为集约式、内涵式增长。

2．经济效益。所选行业应具有一定的经济规模和经济效益。

3．带动性。新经济增长点的推动作用和带动作用要大，能够促进相关产业发展。

结合以上原则，根据理论指导及实际数据来源，本文选择如下指标：

1．反映增长潜力与成长性的指标

经济增长理论认为，决定经济增长的主要因素有技术进步、人力资源和资本积累。根据前言分析，中国现阶段通过投资实现增长已经不可持续，但可以通过鼓励技术进步得到，因此在增长潜力原则下选择技术进步贡献率指标。

技术进步贡献率

x1＝1－（α×K）／Y－（β×L）／Y

其中K为资本的年均增长速度，L为劳动的平均增长速度，α为资本产出弹性，β为劳动产出弹性，通常假定生产在一定时期内α、β为一常数，并且α＋β＝1。

新经济增长点应该适应市场需求，具有巨大的市场潜力，因此选择需求收入弹性系数x2作为反映市场需求标准的指标。该系数是指在价格不变的前提下，某行业的需求增加率同人均国民收入增加率之比，用以反映某行业的社会需求量的变化对国民收入变化的敏感程度。其中x2表示某行业i的需求收入弹性系数；ΔQi／Qi为该产业的需求增加率；ΔNi／Ni为同期人均国民收入增加率，i＝1，2，…，n。

2．反映经济效益的指标

3．反映带动性的指标

新经济增长点对一个时期一个地区经济增长的带动性可以通过影响力系数和感应度系数得以评价。

影响力系数反映了某产品部门最终需求增加一个单位时对国民经济其他部门的影响程度。

感应度系数反映了国民经济的其他部门的最终需求均增加一个单位，各部门应该增加的总产出的数量。

三、实证分析

（一）训练集与实验集样本数据来源

训练集中的训练样本分为两类，一类为“新经济增长点”，另一类为“非新经济增长点”。“新经济增长点”一类选择的是我国信息产业（2010）、汽车产业（2003），这两个行业在相关文献中有所提及并在经济发展中得到检验［9－10］，因此选择信息产业2005—2009年的数据及汽车产业1999—2003年数据；“非新经济增长点”一类选择的是我国水的生产和供应业（2010），为与“新经济增长点”一类保持同比性，数据同样为5年期限，从2006—2010年。指标数据来源于《中国信息产业年鉴》（2006—2010），《中国汽车工业年鉴》（2000—2004），《中国统计年鉴》（2004—2011），《中国投入产出表》（2002，2007），部分指标数据经计算得到。

实验集中的实验样本选择《陕西统计年鉴》（2011）工业分类下的38个部门，数据来源于《陕西统计年鉴》（2005—2011），《中国投入产出表》（2007），《陕西省投入产出表》（2007）。

（二）计算步骤与结果

1．数据无量纲化处理

为了剔除量纲对计算结果的影响，首先对数据进行初始化处理。本文选择的无量纲化方法为标准化处理法m）分别为第j项指标观测值的平均值和标准差，x＊ij为处理后的标准化指标。

2．指标计算

需求收入弹性系数的计算。在利用式（7）对需求收入弹性系数进行实际计算时，对此公式做适当的转化，用某行业的产品收入弹性系数代表该行业的收入弹性系数；公式所指的需求量是指未来的需求量，但因无法提前预知，故用当期的需求量替代；基于对统计数据可得性的考虑，用当期的销售量表示需求量。

技术进步贡献率的计算。技术进步贡献率的计算根据C－D生产函数，ΔA／A＝ΔY／Y－αΔK／K－βΔL／L。式中，ΔA／A为全要素生产率；ΔY／Y为生产增长率，ΔL／L为劳动增长率；ΔK／K为资金增长率；α表示劳动对国民收入所做贡献的百分比，β表示资金对国民收入所作贡献的百分比。本文对陕西省第二产业各行业分别取2005—2011年产值、从业人员数、固定资产数，根据C—D生产函数，其中使用永续存盘法测算固定资本存量，使用SPSS11．0利用多元非线性回归功能计算第二产业各行业的技术进步贡献率。

3．模型拟合

首先，按如下规则设置训练集样本：

（1）设“新经济增长点”信息产业和汽车产业均为“1”；

（2）设“非新经济增长点”水的生产和供应业为“－1”。

模型采用基于径向基函数的SVM分类器，令σ＝0．5。利用式（5），求出相应的（αi，b）及其对应的支持向量，并结合式（6）给出的行业分类模型，计算实验样本中各行业的分类结果。表1给出了以上计算过程的拟合结果。从表1中可以看出，模型将行业分为两类：新经济增长点（13个行业）和非新经济增长点（24个行业）。通过计算各行业实验数据到最优平面的距离（d），可以给出各行业在各自分类中的排名次序规则：d越小，越与训练集中的分类标准相近，该行业越有可能成为（非）新经济增长点。

表1 模型分类及排序结果表

（三）结果分析

经计算可知，被划分为新经济增长点一类的行业为通信设备、计算机及其他电子设备制造业，非金属矿物制品业，石油和天然气开采业，文教体育用品制造业，医药制造业，印刷业和记录媒介的复制，有色金属矿采选业，通用设备制造业，电气机械及器材制造业，专用设备制造业，纺织业，化学纤维制造业，非金属矿采选业。根据行业到最优平面的距离（d）将排在前十位的行业作为重点发展行业。

根据行业增长特点，具体的增长环节分析如下：通信设备、计算机及其他电子设备制造业可发展一些污染小、附加值高、对整个西部辐射作用较大的产业，如高端软件和集成电路产业、物联网产业；通用设备制造业着重发展高新技术产业；有色金属矿采选业注重其中新能源产业的发展；基于陕西省大力发展文化产业的实际情况，印刷业和记录媒介的复制业的发展可侧重于与文化产业相关部分进行结合；医药制造业着重培育在生物产业的生物医药领域中的应用；借陕西省建立国家民用航天产业基地的契机，专用设备制造业也可与之相结合发展；电气机械及器材制造业可着重发展集成电路、激光、半导体照明等产业。《陕西省国民经济和社会发展“十二五”规划纲要》中指出，“十二五”期间陕西省要重点发展装备制造业、文化产业、战略性新兴产业，其中战略性新兴产业包括高新技术产业、能源产业，与本文的分析结果相比，通过支持向量机的方法选择的新经济增长点与陕西省“十二五”规划确定的重点发展产业基本吻合。

四、结 论

本文使用SVM选择新经济增长点，其优势在于：通过经时间证实的增长点挖掘潜在经济增长点，使得模型同时具备经济属性、空间属性和时间上的潜在性。SVM在解决小样本、非线性及高维模式识别方面具有优势，本文使用某个地区在某个时期成为新经济增长点的行业作为新经济增长点判断的“标准行业”，利用SVM在识别时需要训练的特点，使用这些标准行业进行训练，通过训练使模型对新经济增长点的特征有了“记忆”，这时，再使用需要被评价的某地区当下时间段的多个行业输入模型进行运算，当某个行业的特征同经过时间验证的过去的新经济增长点的特征一致或接近时，模型就会识别出来新经济增长点。同时，在选择出新经济增长点后，将行业与本地区的自然资源和行业发展动态相结合，寻找具体的增长环节，完成新经济增长点的微观化，加深对增长环节具体化的理解和研究。

［1］ Perroux F．Economic Space：Theory and Application［J］．Quarterly Journal of Economics，1950（64）．

［2］ 罗亮．国内关于经济增长点理论的研究综述［J］．经济学动态，2003（12）．

［3］ 王志宝．确定新经济增长点的一种方法——以深圳市为例［J］．经济地理，2009（4）．

［4］ 辛杨．新经济增长点开发理论与方法研究［D］．长春：吉林大学管理学院，2006．

［5］ 陈红霞，袁显平．“十二五”产业增长点的选择与评价——以陕西省工业为例［J］．中国科技论坛，2011（6）．

［6］ Vapnik V．The Nature of Statistical Learning Theory［M］．2nd ed．New York：Springer Verlag，1999．

［7］ 郑治伟，孟卫东．基于支持向量机的重庆市主导产业选择研究［J］．北京理工大学学报：社会科学版，2010（10）．

［8］ Muller K R，Mika S，Rtsch G．An Introduction to Kernel－Based Learning Algorithms［J］．IEEE Trans．on Neural Networks，2001，12（2）．

［9］ 赵彤．21世纪中国经济新的增长点［J］．交通科技与经济，2004（3）．

［10］郑小波．我国电子信息产业对国民经济发展的影响力研究［J］．商业时代，2011（25）．

Study about Selection of the New Economic Growth Point Based on Support Vector Machine

ZHANG Qian
（School of Statistics，Xi＇an University of Finance and Economics，Xi＇an 710100，China）

For the problem of selection model of the new economic growth point can not be distinguished between the“existing”and“new”，This paper use SVM to mining the potential economic growth point．Research results show：38industrial sectors of Shaanxi Province in 2010，can be divided into two categories，one is the“new economic growth points”and the other is“non－new economic growth points”．Top 10industrial sectors of the“new economic growth points”category are consistent with the cultural industries，high－tech industries，new energy industry in 12th Five－year Plan of Shaanxi province，it said that SVM is feasible and reliable in the selection of new economic growth points．

new economic growth point；support vector machine；industries

book=66,ebook=12

F061．3

A

1007－3116（2012）06－0066－06

（责任编辑：王南丰）

2012－03－04

西安统计研究院基金项目《加快发展第三产业行业与陕西省新经济增长点研究》（09JD09）

张 倩，女，新疆乌鲁木齐人，硕士，助教，研究方向：统计方法与应用。