非参数固定效应Panel Data模型的分位数回归推断

吕秀梅

非参数固定效应Panel Data模型的分位数回归推断

吕秀梅

（重庆工商大学财政金融学院，重庆400067）

利用分位数回归方法，讨论了非参数固定效应Panel Data模型的估计和检验问题，得到了参数估计的渐近正态性及收敛速度。同时，建立一个秩得分（rank score）统计量来检验模型的固定效应，并证明了这个统计量渐近服从标准正态分布。

分位数回归；渐近正态；固定效应；Panel Data模型

一、引 言

Panel Data是指相同截面上的个体在不同时点重复观测的数据，基于Panel Data的回归模型称为Panel Data模型，Hsiao等都对Panel Data模型作了详细的阐述［1－3］。近几年，Panel Data模型的研究主要集中在非参数和半参数模型的估计和检验上。Lin等使用平滑样条估计和核估计方法研究非参数Panel Data模型，推导出了样条估计量与核估计量的渐近偏差和协方差［4］；Li和Stengos借助工具变量对半参数线性Panel Data模型进行估计，并且证明当T很小，N很大时，估计量以槡N一致收敛［5］；Li和Hsiao给出半参数Panel Data模型三个检验序列相关的统计量，并且证明这些统计量分别渐近服从正态分布或卡方分布［6］。与此同时，非参数与半参数Panel Data模型的广泛应用使它备受理论界和实务界的重视，得到了统计学家和经济计量学家在理论和应用上的深入研究，并且在经济学领域的应用逐渐被经济计量学家所推广。

现有的大多数文献都是使用最小二乘法或Profile似然法对Panel Data模型进行估计和检验，但是上述方法严重依赖于随机误差项方差的结构，而分位数回归对这一要求较弱，它只要求随机误差项的τ∈［0，1］分位数存在，因此本文采用分位数回归方法来研究非参数固定效应Panel Data模型。以分位数回归方法来研究统计或经济模型已经成为研究的热点。李育安介绍了分位数回归法的概念、算法及主流统计软件R和SAS计算时的语法，并通过实例与线性回归进行了对比，展现了分位数回归的巨大魅力［7］；Kim使用分位数回归研究变系数模型的估计和检验，得出了参数估计的渐近理论和检验统计的分布性［8］；Wang H．X．J．和Wang L．使用加权分位数方法研究坍塌回归模型，给出了参数估计的一致性和渐近正态性［9］；Cai和Xu研究了非参数动态光滑系数模型的非参数分位数估计，给出估计的正态性及估计量在边界上的渐近行为［10］；张涛通过分位数回归方法，利用CHNS 2006年的数据，从教育回报率、性别和工作部门的差异三个方面对中国工资收入差异进行研究［11］。

本文考虑如下非参数固定效应Panel Data模型：

其中（yit，xit）是第i个个体在t时刻因变量与自变量的观测值，αi是固定效应，f（·）是未知的光滑函数。εit是独立同分布的误差项，满足零均值，并且假定对任意的i，t，εit与αi，xit相互独立。为了模型的可识别，本文要求αi满足

对于模型（1），Hendersona等运用非参数估计迭代法对该模型进行估计，并把这种估计方法运用于固定效应半参数模型，同时对非参数Panel Data模型里的固定效应进行了零假设检验，但是文中并没有给出检验统计量的分布性［12］；Su和Ullah运用Profile似然估计方法，给出了估计量的收敛速度和渐近正态性，但并没有解决固定效应的检验问题［13］；魏传华和吴喜之采用Profile最小二乘法讨论了该模型的估计与检验方法，得到固定效应与非参数部分的估计［14］，同时给出了计算检验P值的F分布逼近法，但是文中只给出了一些估计方法，并没有获得参数估计的渐近理论，也没有推导检验统计量的分布性。本文应用分位数回归方法，不仅得出了参数估计的收敛速度和正态性，而且建立了一个检验固定效应的统计量，并证明了这个统计量服从标准正态分布。

二、分位数估计

定义模型（1）的τ分位数为：

这里假定随机项εit的τ分位数等于0。

由于fτ（xit）是一个未知光滑函数，因此本文假定fτ（xit）有如下形式的级数展式：

其中｛Pl，τ（xit）是定义在RK空间上的基函数｛θl｝K

l＝1对应的参数。

分位数估计参数（ατi，θτl）是通过极小化

得到的，这里ρτ（a）＝a（τ－I（a≤0）），并且I（A）是一个定义在集合A上的示性函数。

为了表达方便，令：

PK，τ（xit）＝（P1，τ（xit），…，PK，τ（xit））′

这里“′”定义为矩阵或向量的转置运算。同时定义：

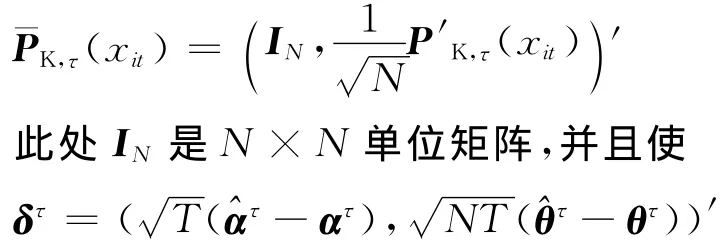
这里

在给出模型（1）的分位数估计的渐进理论时，需要以下假设条件［8－9，15］。

条件1 fεit（0）＞0且fεit（s）在零的领域Lipschitz连续。

条件2 非参数函数fτ（xit）有如下分解式：

条件3 ρτ（s）是一个凸函数，并且满足E（ψ（eit））＝0，E（ψ（eit））2＜∞，这里ψτ（a）＝τ－I（a≤0）。

条件4 存在正常数c2，c3和c4，使得

E（ψτ（eit＋s）－ψ（eit））2≤c2｜s｜

并且｜ψτ（v＋s）－ψτ（v）｜≤c3，对所有｜s｜≤c4成立，这里s，v∈R。

在介绍定理1前，先给出两个有用的引理，它们的证明与Cai和Xu的方法类似［10］。

引理1 如果一个向量函数Vn（Δ）满足

（1）－Δ′Vn（λΔ）≥－Δ′Vn（Δ），对任意的λ≥1；

（

2）sup‖Vn（Δ）＋DΔ－An‖＝o（1），这里

‖Δ‖≤M‖An‖＝o（1），0＜M＜∞且D是非随机矩阵；

（3）Δn是一个满足‖Vn（Δn）‖＝o（1）的向量，则‖Δn‖＝o（1）且Δn＝D－1An＋o（1）。

引理2 当假设条件1～4成立时，对向量函数QN，T（Δ1，Δ2），有

‖QN，T（Δ1，Δ2）－QN，T（Δ1，0）－E（QN，T（Δ1，Δ2）－QN，T（Δ1，0））‖＝o（1）

及

‖E［QN，T（Δ1，Δ2）－QN，T（Δ1，0）］＋Φ珦NΔ2‖＝o（1）

其中

并且

这里Δ1＝bτij并且Δ2＝δτ。

定理1 在假设条件1～4成立时，有：

其中W＝diag｛fεit（0）｝和PK，τ（x）是一个N×T矩阵，其第i，j个元素为｛PK，τ（xij）｝。

证明：首先

AN，T＝QN，T（Δ1，0）

由条件1知：

接着考虑

因此可以得到：

＝ΦN

并且

三、假设检验

在固定效应Panel Data模型中，一个实际问题就是检验模型中的固定效应是否对模型产生影响，因此建立了一个基于分位数检验的秩得分（rank score）统计量，来检验原假设固定效应不会在模型中产生影响，即H0∶αi＝0。

首先作如下定义：

PK，τ（xi）＝（PK，τ（xi1），…，PK，τ（xiT））′

PK，τ（x）＝（PK，τ（x1），…，PK，τ（xN））′

ψτ（＾ei）＝（ψτ（＾εi1），…，ψτ（＾εiT））′

ψτ（εi）＝（ψτ（εi1），…，ψτ（εiT））′

ΣNT＝E（P′K，τ（x）PK，τ（x））

定理2 在假设条件1～4及原假设H0成立时，有

证明：令γ＊＝P′K，τ（x）γτ，＾γ＊＝P′K，τ（x）＾γτ，珘γ＝＾γ＊－γ＊，Γit＝PK，τ（xit）／PK，τ（x），并且对任意的常数L定义γ☆L＝｛γ＊｜γ＊∈RNT，｜γ＊｜≤LK1／2｝。

类似Kim的做法［8］，在设条件1～4成立时有：

由此可得，P｛｜＾γ＊－γ＊｜≤LK1／2｝＞1－ε，即｜＾γ＊－γ＊｜2＝O（K）。故｜＾γτ－γτ｜2＝O（K／（NT））。

因此只需证明＾SN，T→SN，T即可。事实上，对任意的ζ＞0和一个足够大的常数C＜∞，可以得到：

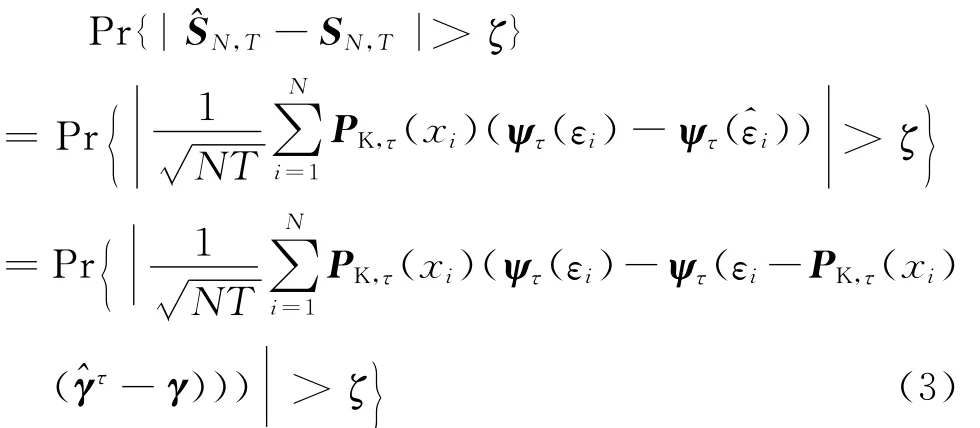
由Chebychev不等式及假设条件4可知，式（3）不大于

因此，由假设条件2和定理2可知，式（4）不大于O（K2／T）O（K／（NT））＝O（1／）＝o（1），于是结论成立。

［1］ Hsiao C．Analysis of Panel Data［M］．2nd ed．Cambridge：Cambridge University Press，2002．

［2］ Baltagi B H．Econometrics Analysis of Panel Data［M］．2nd ed．New York：Wiley，2005．

［3］ 白仲林．面板数据模型的设定、统计检验和新进展［J］．统计与信息论坛，2010，25（10）．

［4］ Lin X，Wang N，Welsh，et al．Equivalent Kernels of Smoothing Splines in Nonparametric Regression for Clustered／Longitudinal Data［J］．Biometrika，2004，91（1）．

［5］ Li Q，Stengos T．Semiparametric Estimation of Partially Linear Panel Data Models［J］．Journal of Econometrics，1996，71（1）．

［6］ Li Q，Hsiao C．Testing Serial Correlation in Semiparametric Panel Data Models［J］．Journal of Econometrics，1998，87（2）．

［7］ 李育安．分位数回归及应用简介［J］．统计与信息论坛，2010，25（3）．

［8］ Kim M．Quantile Regression with Varying Coefficients［J］．The Annals of Statistics，2007，35（3）．

［9］ Wang H X J，Wang L．Locally Weighted Censored Quantile Regression［J］．Journal of the American Statistical Association，2009，104（487）．

［10］Cai Z W，Xu X P．Nonparametric Quantile Estimation for Dynamic Smooth Coefficient Models［J］．Journal of the American Statistical Association，2009，104（485）．

［11］张涛．工资收入差异的解释：基于分位数回归的经验研究［J］．统计与信息论坛，2011，26（11）．

［12］Hendersona D J，Carrollb R J，Li Q．Nonparametric Estimation and Testing of Fixed Effects Panel Data Models［J］．Journal of Econometrics，2008，144（1）．

［13］Su L，Ullah A．Profile Likelihood Estimation of Partially Linear Panel Data Models with Fixed Effects［J］．Economics Letters，2006，92（1）．

［14］魏传华，吴喜之．非参数固定效应Panel Data模型的统计推断［J］．数理统计与管理，2009，28（4）．

［15］He X M，Shi P D．Bivariate Tensor－product B－splines in a Partly Linear Model［J］．Journal of Multivariate Analysis，1996，58（2）．

Inference for Quantile Regression in Nonparametric Panel Data Model with Fixed－Effects

LV Xiu－mei
（School of Finance，Chongqing Technology and Business University，Chongqing 400067，China）

Using quantile regression methods，a nonparametric panel data model with fixed－effects is estimated and tested，the convergence rates and asymptotic normality of estimated parameters are obtained．Moreover，a test statistic named rank score is proposed for the fixed－effects and is proved to obey standard normal distribution．

quantile regression；asymptotic normality；fixed－effects；panel data model

book=28,ebook=47

O212．7

A

1007－3116（2012）06－0028－05

（责任编辑：崔国平）

2011－12－04

教育部科学技术研究重点项目《非线性粘性Boussinesq系统的适应性与数值解研究》（109140）

吕秀梅，女，四川德阳人，经济学博士，讲师，研究方向：金融计量，经济模型识别。