基于TSVD正则化方法的概率密度估计

吴 笛，刘 文

(武汉理工大学理学院，湖北武汉 430070)

概率密度估计既是传统的概率论与数理统计的重点，也是统计学习理论的重要研究内容［1］。在解决统计学习问题的传统模式中，模式识别和回归估计都建立在密度估计的基础之上［2］。且概率密度估计在实际中有广泛的应用，如电子器件寿命估计和排队论等。但在实际应用中很多时候并不知道概率密度的分布，这时可根据样本点进行回归分析得到实际概率密度的一个近似估计。目前的概率密度估计方法主要分为参数估计和非参数估计两大类。参数估计方法具有较大的局限性，其前提是已知数据密度符合某种分布，但问题在于如何确定密度函数中的参数，这种方法强烈依赖于前提假设，一旦假设错误，估计值就无法较好地反映真实值。非参数估计具有更广的应用范围，并且已经得到了广泛研究，提出了核估计和近邻估计等方法。然而上述方法需要用到所有的训练样本以估计出概率密度，当训练样本非常多时，计算量非常大并不实用［3］。长期以来，人们希望寻求一种既可减少计算量又可保持估计精度的求解方法。正则化理论［4］的引入较好地解决了这一问题，利用惩罚项来得到偏移-方差平衡，防止概率密度过度拟合的发生。笔者将概率密度的估计转化成一类线性算子方程问题的求解，并根据算子方程核矩阵奇异值的性质，构建了概率密度估计的TSVD正则化方法［5-7］，同时将其与估计概率密度的K+线性Bregman迭代正则化方法［8-10］进行比较分析。

1 概率密度估计问题的描述

根据概率密度的定义，密度估计是一个求解第一类Fredholm积分方程的问题，如:

对式(1)，概率密度函数p(x)须同时满足如下条件:

在实际应用中，往往只考虑区间［a，b］上的概率密度估计问题，对于已知的独立同分布数据x=(x1，x2，…，xM)，此时的经验分布函数 FM(x)可由x来构造，即:

其中指示函数θ(x)为:

笔者的目的是将概率密度估计问题转化为线性算子方程，然后利用截断奇异值分解(truncated singular value decomposition，TSVD)方法进行求解。根据式(2)～式(4)的定义，可将式(1)离散成如下的线性算子方程:

其中，核矩阵K为0-1矩阵。在实际问题中右端项F(x)通常包含噪声，给右端项F(x)一个很小的扰动都会使得式(5)的解产生巨大的震荡现象，无法对概率密度函数p(x)进行准确估计。这时式(1)和式(5)就变为一个不适定问题。因此，笔者将采用计算量较小的TSVD正则化方法估计概率密度函数p(x)。

2 基于TSVD的概率密度估计

2.1 概率密度估计的TSVD正则化方法

假设实际观察中式(5)右端项为Fδ(x)，则:

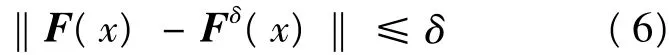
其中，δ为误差水平。

根据核矩阵K基于指示函数θ(x)的定义，对核矩阵K进行奇异值分解(singular value decomposition，SVD)，以便分析其性质，构建求解式(5)的正则化方法。以100×100大小的核矩阵K为例，对应奇异值的分布情况如图1所示。

图1 核矩阵K(100×100)奇异值的分布情况

由图1可知，核矩阵K的能量主要集中在少数几个数值较大的奇异值上。KIRSCH指出不适定问题解的不稳定性的根源在于紧算子的奇异值有趋于零的性质，由此引入TSVD正则化方法来减弱或滤掉奇异值趋于零的性质对解的稳定性影响，并对核矩阵K进行奇异值分解得到:

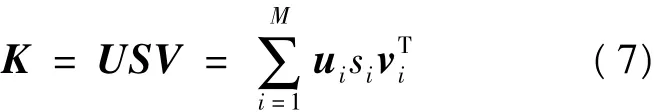
其中，奇异值 si=S(i，i)(i=1，2，…，M)，且ui和vi分别为酉矩阵U和V的行向量，满足以下性质:

根据式(7)，此时式(5)可转化为:

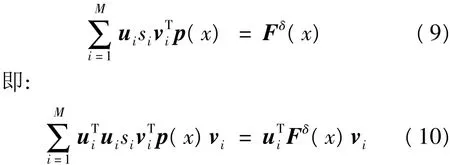
利用行向量ui和vi的性质，根据式(9)和式(10)可求得概率密度函数为:

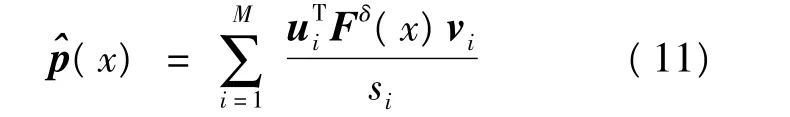
式(11)中的奇异值si随着i增加逐渐趋于0，而1/si将趋于无穷大。此时式(5)的解不连续依赖于右端的数据，当右端数据F(x)存在误差时，方程的解与真解间存在较大的误差，无法得到准确的概率密度函数p(x)。因此，有必要在保证概率密度函数估计值满足ε的基础上，对奇异值si进行截断来保证方程解的稳定性，则此时的概率密度函数估计值为:

其中，k(1≤k≤M)为正则化参数，以控制奇异值si的截断。

2.2 TSVD正则化方法的收敛性分析

研究重点在于根据概率密度的定义，将概率密度的估计转化成第一类Fredholm算子方程的求解问题，然后利用能保证正则解误差具有渐进最优阶的TSVD正则化方法进行求解，以体现TSVD正则化方法在处理概率密度估计问题中的优越性。对于TSVD正则化方法的误差估计、正则化参数先验选取及其收敛性和收敛阶分析，黄小为等已作了深入研究。针对式(5)，其给出了TSVD正则化方法在概率密度估计问题中的收敛定理1。

定理1 设式(5)的精确解p+(x)=(K*·K)vz∈R(K*K)v，z∈X(p)且‖z‖2≤E，则对于TSVD正则化方法，若选取正则化参数k=k(δ)使得成立，则有:

其中:K*为K的伴随算子;为概率密度的估计值;E∈R为常数;X(p)为实Hilbert空间，且满足p(x)∈X(p)。该定理说明，TSVD正则化方法可保证概率密度估计值的误差具有渐进最优阶，且数值计算简单易行，其具体证明过程及相关性质分析请参见文献［5-6］。

3 实验结果及分析

由式(13)产生100个服从正态分布的随机样本:

其中，均值分别为μ1=0和μ2=2，标准差分别为 σ1=1和 σ2，变量 x的取值范围为［-5，5］。

为了加快求解式(14)的收敛速度，在此利用K+线性Bregman迭代正则化方法对其进行求解，具体迭代过程如下:

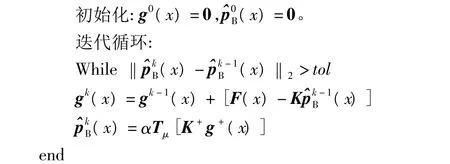
其中，K+=KT(KKT)-1，参数 α ＞0，μ ＞0，并定义向量阈值算子为:

根据前文对TSVD正则化方法的介绍，得到求解概率密度函数的TSVD方法的迭代过程如下:

迭代循环:

假设右端数据F(x)分别受均值为0，方差为0.001、0.010和0.050的高斯白噪声的干扰，并利用线性Bregman迭代正则化方法和TSVD正则化方法分别对式(5)进行求解。其中线性Bregman迭代正则化方法中的参数分别为α=0.8和μ=0.005，则实验结果如图2和表1所示。

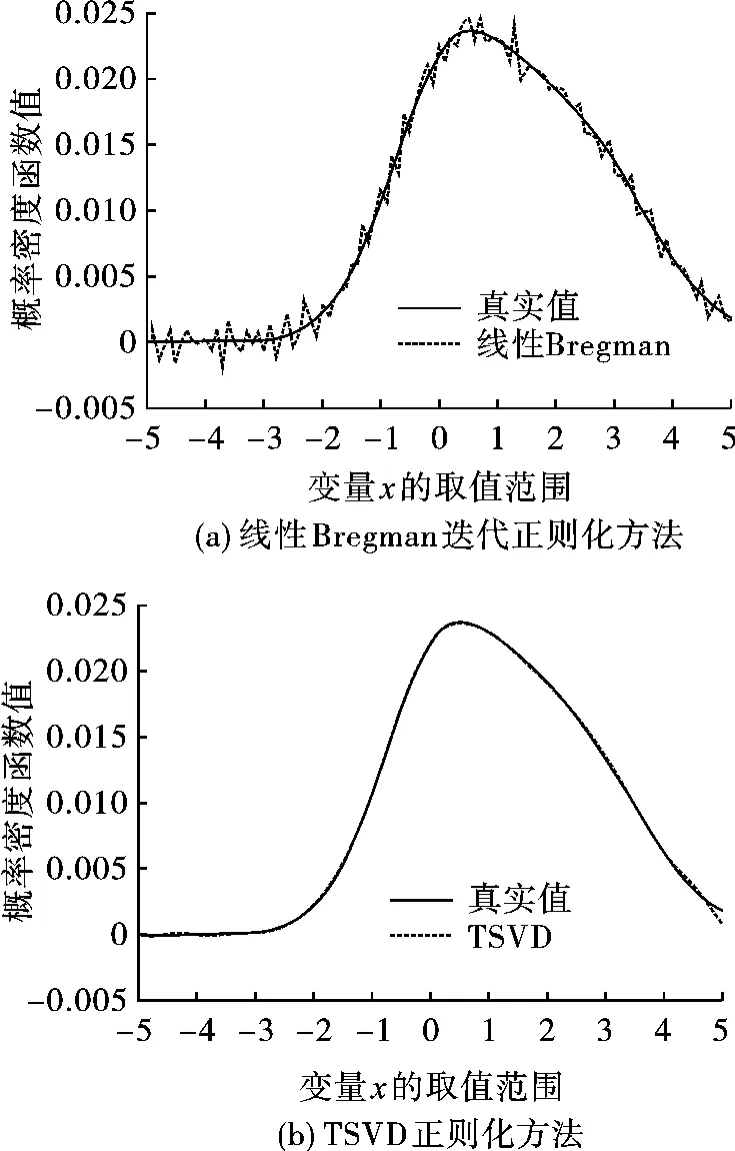
图2 实验结果比较分析(噪声方差为0.001)

由图2可知，当式(5)的右端项F(x)受噪声干扰时，TSVD正则化方法可以较好地估计概率密度函数pT(x)，而K+线性Bregman迭代正则化方法易受噪声的干扰，估计的概率密度函数pB(x)存在较为明显的波动，不能较好地逼近真实的概率密度函数p(x)。由表1可知，当噪声方差分别为0.001、0.010和0.050时，基于 TSVD的概率密度估计要好于线性Bregman迭代正则化方法，显示出更强的稳定性，且更易于编程实现。

表1 线性Bregman与TSVD的实验结果比较

其中，假设 f∈IRN:=IR{1，2，…，N}，对于 1≤p ＜∞，则lp范数可定义为:

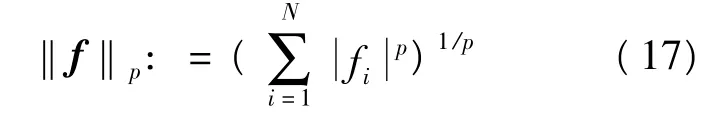
4 结论

笔者在分析核矩阵K的奇异值性质的基础上，构建了概率密度估计的TSVD正则化方法，将概率密度估计问题转化成l1正则化问题，并构建了求解该最优化问题的K+线性Bregman迭代正则化方法。由实验结果可以看出，用TSVD估计的概率密度可以较好地逼近真实的概率密度，较线性Bregman迭代正则化方法表现出更好的估计效果，且更易于编程实现，在不同噪声水平下表现出更强的稳定性。

［1］VLADIMIR N V.统计学习理论的本质［M］.张学工，译.北京:清华大学出版社，2000:12-98.

［2］VLADIMIR N V.统计学习理论［M］.许建华，张学工，译.北京:电子工业出版社，2004:87-125.

［3］FUKUNAGA K，HAYES R R.The reduced Parzen classifier［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(4):423-425.

［4］ENGL W，HANKE M，NEUBAUER A.Regularization of inverse problems［M］.Dordrecht:Kluwer Acdemic Publishers，1996:19-76.

［5］黄小为，吴传生，朱华平.求解不适定问题的TSVD正则化方法［J］.武汉理工大学学报，2005，27(2):90-92.

［6］黄小为，吴传生，李卓球.TSVD正则化方法的参数选取及数值计算［J］.华中师范大学学报:自然科学版，2006，40(2):154-157.

［7］BOUHAMIDI A，JBILOU K，REICHEL L，et al.An extrapolated TSVD method for linear discrete ill-posed problems with Kronecker structure［J］.Linear Algebra and its Applications，2011(7):1677-1688.

［8］CAI J F，OSHER S，SHEN Z W.Linearized Bregman iterations for compressed sensing［J］.Mathematics of Computation，2009(78):1515-1536.

［9］张慧，成礼智.A-线性Bregman迭代算法［J］.计算数学，2010，32(1):97-104.

［10］YIN W T，OSHER S，GOLDFARB D，et al.Bregman iterative algorithms for l1-minimization with applications to compressed sensing［J］.SIAM Journal on Imaging Sciences，2008，1(1):143-168.