自适应非线性BSS及其在齿轮故障诊断中的应用

王晓伟，石林锁

(第二炮兵工程大学 502教研室，西安 710025)

盲信号处理(Blind Source Separation，BSS)是指在未知源信号和传输通道参数的情况下，仅由传感器阵列获得的观测信号恢复出各源信号的过程。其在无线通信、雷达信号处理、地质勘探和生物医学信号检测方面有着广泛的应用前景和价值［1］，近年来也越来越广泛地应用于机械设备状态监测和故障诊断中［2-3］。

当前应用盲信号处理技术进行机械故障诊断，绝大部分是假设源信号是线性混叠的，然而在实际中非线性的情况是广泛存在的［4］，混叠模型更多的情况应该是非线性或者弱非线性的。传统的非线性盲信号处理算法的学习速率是固定的［5-6］，学习速率选择的过大或过小，都将影响算法收敛的精度和速度。最佳分离结果通常对应于目标函数的极值点，然而目标函数通常存在很多的局部极小值点，这就会导致算法在局部极小值点收敛，从而陷入局部最优解，难以获得全局最优解。

本文将模拟退火算法与基于核函数的非线性盲处理算法相结合，提出一种基于核函数的自适应非线性盲处理算法，以提高非线性盲信号处理的收敛精度和全局寻优能力，进而提高信号特征提取的效果。通过仿真和实测齿轮箱振动信号的实验，表明与传统的非线性盲处理算法相比，该算法具有更好的消噪和信号特征提取能力。

1 非线性BSS问题

设源信号 s=［s1(t)，s2(t)，s3(t)，…，sN(t)］T零均值统计独立，则非线性瞬时混合模型可表示为［7］：

式中：x(t)=(x1(t)，x2(t)，x3(t)，…，xM(t))T为传感器测得的M维数据向量，f(·)为未知的可逆实值非线性混合函数，n(t)是与源信号统计独立的加性信号。为简单起见，通常假设独立源个数N等于混合信号的个数M，并取n(t)=0。那么非线性盲源分离问题就是仅通过观测信号x(t)及源信号统计独立的假设条件来找到一个映射 h(·)，使得 x(t)通过 h(·)可以恢复源信号s(t)。分离系统的输出信号为：

式中：y(t)即为s(t)的估计。

上述非线性模型的一种特殊情况——后非线性混合模型，可以描述如下［8］：

式中：f(·)是一固定可逆非线性函数，A为线性非奇异矩阵，这样源信号先经过典型线性混合过程，然后通过非线性函数f(·)作用而形成最后的观测x(t)。在许多实际信号处理中，后非线性模型可看作传感器畸变测得的信号。

后非线性混合模型的分离过程与混合过程正好相反，即先通过可逆的非线性变换 h(·)得 v=h(x(·))，然后再对v进行线性变换W，得到源信号的估计y(t)。如果h(·)和W分别是f(·)和A的逆变换时，源信号就得到恢复。上述过程可简单表示为：

非线性去混函数h(·)的选取与f(·)相对应，两者要能满足互逆或近似互逆的关系。但到目前为止，还没有一种函数可以拟合任意非线性函数的逆函数。更重要的是非线性函数h(·)是未知的，且在不知道原始信号样本情况下，如用神经网络进行训练逼近也非常困难。

2 基于核函数的非线性盲处理算法

核函数方法首先是在支持向量机领域中获得了成功的应用，其思想就是用非线性变换Ψ ∶ϑ→Γ将输入的数据x(t)∈ϑN映射到特征空间Γ中［5］：

特征空间中的点积可以由核函数计算得到，即：

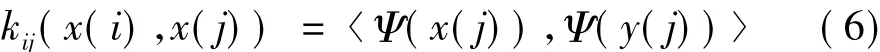
可以证明，分离矩阵可以表示成公式：

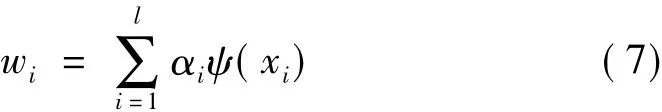
分离矩阵的求解转化为参数α的求解，目标函数表示为［9］：

3 基于模拟退火的改进非线性盲信号处理

模拟退火算法是以马尔科夫链的遍历理论为基础的一种随机寻优算法［10］。算法的核心在于模拟金属溶液的冷却结晶过程，其过程由某一较高初始温度开始，利用具有概率突跳特性的Metropolis抽样策略在解空间中进行随机搜索，伴随温度的不断下降重复抽样，在退火温度的控制下最终找到全局最优解。由于采用了Metropolis准则，中间解以一定的接受概率接受较差点，从而可以跳出局部极小，避免落入局部极小点的可能［11］。如果初始温度足够高，温度下降足够慢，算法能以概率1收敛到全局最优值。

模拟退火算法的特点是整个迭代过程可通过退火历程(即初温、退温函数、抽样次数)加以控制。控制初温，可控制算法的初始搜索行为。控制温度的高低，可控制算法突跳能力的强弱：高温下的强突跳性有利于避免陷入局部最优，低温下的趋化性寻优有利于提高局部搜索能力。控制温度的下降速率，可控制突跳能力的下降幅度，影响搜索过程的平滑性。控制抽样次数，可控制各温度下的搜索能力，影响搜索过程对应的齐次马氏链的平稳概率分布。

基于模拟退火思想的改进非线性盲信号处理的步骤为：

(1)给定冷却进度表参数及迭代初始解，初始化参数α，计算目标函数值Fα。

(2)初始化温度T0，令T0=Fα，初始化退火速度λ和最大退火次数，这里取λ=0.99。

(3) 对于某一温度t，采用方程T(t)=T0·αt进行退火。按步骤(4)到步骤(6)进行迭代，直到达到最大退火次数，跳到步骤(7)。

(4)在当前参数邻域内进行随机扰动，产生新的参数 α'，计算新的目标函数 Fα'。

(5)计算新的目标函数值和当前目标函数值的差 ΔF。

(7)判断是否达到最大退火次数。是，则结束算法，输出分离结果，否则返回步骤(3)继续迭代。

4 仿真信号实验

首先以传感器畸变信号(即后非线性模型)的分离为例来验证本文算法的性能，选取的源信号数目为2，采用下式给出的信号，n(t)为均值为零，方差为5的高斯白噪声。其波形如图1所示。

线性变换矩阵 A随机产生，非线性函数 f(·)为tanh(·)函数，混合后得到观测信号x(t)如图2所示。

图3和图4分别为传统的非线性盲分离和用本文改进的非线性盲分离算法得到的y(t)的时域图。

图1 源信号时域波形图Fig.1 Time domain waveform of source signals

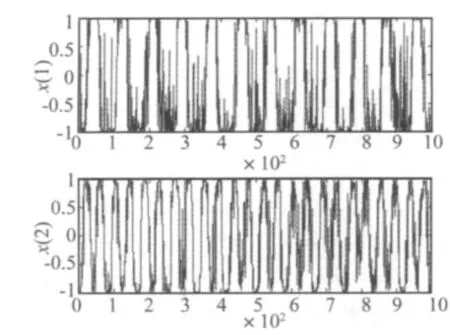
图2 混合信号时域波形图Fig.2 Time domain waveform of mixed signals

对改进的非线性盲信号处理算法进行评价，可采用相似系数ζ评估分离后的时域波形值与源信号之间的相关性，定义如下：

图3 传统的非线性盲分离信号Fig.3 Signals separated by traditional algorithm

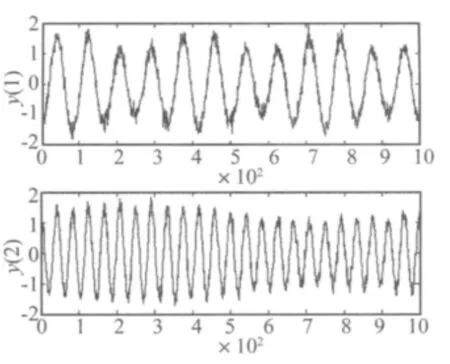
图4 本文的自适应盲分离信号Fig.4 Signals separated by the improved algorithm

5 基于核函数的非线性盲分离的齿轮箱诊断

下面应用基于核函数的自适应非线性盲分离算法进行实验。我们采用的系统是RIDC-Ⅱ型齿轮箱模拟故障实验台，系统由主要由直流电机、齿轮减速器、加载电机及直流调速加载系统组成。因为组成实验台的零部件比较多，传感器拾取的信号必然是各振动源经过传输路径，并且混有噪声的复杂的混合信号。基于后非线性混合模型，应用基于核函数的盲信号处理的方法将各独立振动源信号分离开来，对分析机械状态特征或故障特征大有益处。

图5 实测时域信号Fig.5 Time domain waveform of practical signals

对齿轮减速箱的中间轴人为设置断齿故障。试验时，输入轴转速为780 r/min，两级传动比为64/26，85/40，采样频率为10.2 kHz，，采用两个加速度传感器测得信号x1(t)和x2(t)，图5显示的为其前1.5 s的时域振动加速度波形图。其频谱为X1、X2，如图6所示。

图6 实测信号频谱图Fig.6 The spectrum of practical signals

图7 本文算法诊断结果Fig.7 Diagnosis result of the improved algorithm

将此观测信号用本文提出的改进算法进行盲源分离，对分离出的信号运用包络解调技术进行分析处理［12-13］，其频谱图如图7所示。图8为传统的固定速率非线性盲源分离得到的信号的包络频域图。由于关注的是信号分离实验及故障诊断的效能，所以对谱值的物理意义不特别说明。

比较两者的时域波形和频域图，可以发现，虽然从图7和图8中都可以发现在断齿轴的转频6.7Hz处，但是图7的信号的频谱特征和噪声控制，比图8有明显改进。故改进的自适应非线性盲处理算法能对机械设备的非线性混合进行更准确的映射。

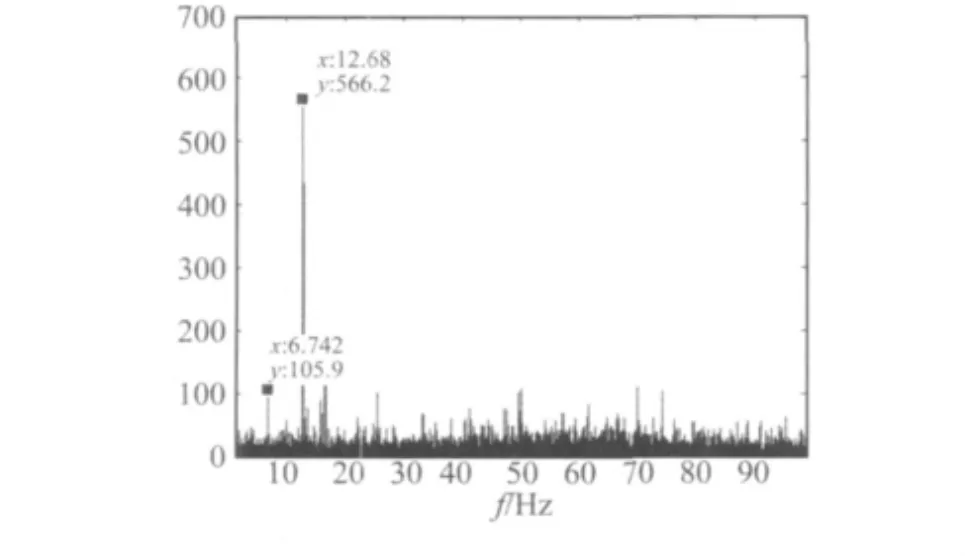
图8 传统算法诊断结果Fig.8 Diagnosis result of the traditional algorithm

6 结论

在对机械振动信号进行分离时，基于核函数的非线性盲处理算法是一个实际而有效的方法。本文针对其学习速率固定的缺陷，将模拟退火算法与基于核函数的非线性盲处理算法相结合，提出一种自适应非线性盲处理算法。这不仅提高了非线性盲处理的效率，而且降低了提取的振动特征信号的噪声。依据自适应非线性盲分离算法得到的分离信号可以更加精确地显示出了齿轮的故障的状态，更有利于对机械设备运行状态的监测和故障诊断。

［1］ Haykin S.Unsupervised adaptive filtering，vol 1：Blind source separation［M］.New York，2000：64-65.

［2］叶红仙，杨世锡，杨将新.基于EMD-SVD-BIC的机械振动源数估计方法［J］.振动、测试与诊断，2010，30(3)：330-343.

［3］范 涛，李志农，卢纪富，等.基于变分贝斯独立分量分析的故障源盲分离［J］.噪声与振动控制，2010，30(1)：82-85.

［4］ Hyvärinen A，Karhunen J，Oja E.Independent component analysis［M］.New York，2001.

［5］Martinez D，Bray A.Nonlinear blind source separation using kernels［J］.IEEE Trans. on Neural Networks.2003，14(1)：228-235.

［6］ Tan Y，Wang J.Nonlinear blind source separation using higher order statistics and a genetic algorithm［J］.IEEE Transactions on Evolutionary Computation(S1089-788X)，2001，5(6)：600-612.

［7］ Cardoso J F.Blind signal separation：Statistical principles［J］.Proc.IEEE，1998，86(10)：2009-2025.

［8］Tong L，Soon C V，Huang F Y.A new blind identification algorithm［J］.In International Conference on Acoustics，Speed and Signal Processing，1990：1784-1787.

［9］马建仓，石庆斌，赵述元，等.机械振动信号非线性混叠的盲源分离［J］.噪声与振动控制，2008，28(6)：5-8.

［10］ Kirkpatrick S，Gelatt C D，Vecchi M P.Optimization by simulated annealing［J］.Science，1983，220(4598)：671-680.

［11］ Fabera R.Dynamic optimization with simulated annealing［J］.Computers and Chemical Engineering，2009，29(2)：273-290.

［12］丁 芳，高立新，崔玲丽，等.共振解调技术在设备故障诊断中的应用［J］.机械设计与制造，2007(11)：178-179.

［13］胡晓依，何庆复，王华胜，等.基于STFT的振动信号调制方法及其在轴承故障检测中的应用［J］.振动与冲击，2008，27(2)：82-86.