水下目标在水下爆炸作用下的毁伤指标研究
2012-09-08张志华梁胜杰胡俊波
李 万,张志华,梁胜杰,胡俊波
(海军工程大学 兵器工程系,武汉 430033)
炸药在水下爆轰瞬间产生的能量可以使爆炸产物气泡瞬时达到高温高压,产生的冲击波、气泡和压力波等会对水下目标造成毁伤。因此人们十分关注水下爆炸对水下目标的毁伤效果的研究,其研究成果广泛应用于民用和军事领域,如在民用上通过水下检测仪器的抗毁伤研究,可以确定临近水下设施的安全距离;在军事上通过研究舰船的抗毁伤[1-2],可以确定船体的薄弱环节从而进行改进;而深入研究水下目标的抗毁伤,不仅在反舰作战时,能有效增强水中兵器抗毁伤能力,同时也能在反水中兵器攻击中发挥重要作用。
对水下爆炸比较系统的研究可以追溯到库尔于1949年出版的《水下爆炸》[3],该书论述了水下爆炸的基本物理现象以及传播机理。随着计算机的高速发展,采用建立动力学方程并进行数值计算,模型试验和数值计算[4-6]成为研究者常用的研究手段,这样可以节省试验经费提高效率。黄晓明等[7]对建立的箱型梁模型在近距水下爆炸作用下的中垂破坏模式进行了试验研究,张振华等[8]利用有限元程序MSC.DYTRAN中强大的流固耦合功能研究船体的结构毁伤,牟金磊等[9]利用有限元软件ABAQUS/EXPLICIT计算固支方板破口大小。然而,在实际之中,特别是水下目标,人们积累的经验很少,边界条件难以确定以及毁伤机理十分复杂,利用数值仿真难以实现,为避免数值计算,研究者常采用毁伤指标来描述目标的毁伤效果,姚熊亮等[10-12]采用不同的冲击因子指标来分析结构毁伤情况;张志华等[13]根据试验获得的加速度峰值指标,利用统计的方法对目标毁伤的有效性问题进行定量分析,给出了目标毁伤曲线。为了描述毁伤效果,还有利用冲击波速度峰值、冲击波压力峰值等指标来表征毁伤程度,但针对不同的毁伤目标,如何客观全面的选择有效毁伤指标集是目前急需解决的问题。
本文针对某水下目标传感器毁伤的抗爆炸试验数据,通过对其毁伤指标如加速度峰值和速度峰值指标的分析,研究这些指标之间的相关关系,在此基础上进一步利用高维压缩方法,确定影响水下目标毁伤的主要特征指标集,揭示水下目标毁伤的影响机理,为客观全面准确地描述毁伤效果奠定基础。
1 水下目标的抗毁伤爆炸试验
1.1 水下爆炸对目标毁伤的毁伤指标
水下爆炸对水下目标的杀伤机制研究主要是依靠水下爆炸冲击波载荷对其外壳或传感器造成冲击毁伤,使传感器失灵而失效。
炸药在水下爆炸时,通常产生冲击波、气泡和压力波。高温高压气泡强烈挤压周围的水并向外扩散,于是便形成了初始冲击波。冲击波传播的同时还会伴随有气泡的脉动作用,并产生二次压力波,也会对目标造成破坏作用。但是由于脉动压力幅值较小,且作用时间较长,在爆炸瞬态动力响应分析时,气泡脉动产生的影响可不予考虑。与此同时,爆炸破片速度在水中衰减得很快,它也很难在一定距离上对水下目标造成毁伤。所以水下爆炸对水下目标的毁伤主要依靠冲击波[14]。
针对某种传感器而言,在水下爆炸的冲击作用时,由于其外壳的防护作用,如果想通过冲击波在水下传播、流固耦合和空气传播的过程建立动力学方程进行数值求解将会非常困难,此时需要选择合适的毁伤指标来分析目标的毁伤效果。传感器在冲击作用时会造成如根部脱掉、底座螺钉松动、联接点断裂、元器件失效、波形产生漂移和电路板移位等多种毁伤模式,为正常反映传感器受冲击和振动的数据,一般选择测量传感器加速度和速度[15]作为毁伤指标来反映水下目标受冲击的程度。加速度和速度一般分为轴向、径向和周向3个方向,为全面描述反映传感器毁伤效果,在实验中选择这3个方向的加速度峰值和3个方向的速度峰值作为需要测量的数据。
1.2 试验方案和数据收集
试验在大型水下爆炸试验水池中进行,考察小药量炸药的水下爆炸对某水下目标的毁伤效果。该水池水面直径85 m,池底直径10 m,水深15 m,呈倒圆台型。将目标固定在水下8 m处。考虑到工程实际,在试验中的药包以2 kg球铸装TNT药包作为标准药包,由于是小药量炸药爆炸,本试验中的自由表面和水底的影响可忽略,可近似认为炸药在无限、均匀、静止的水介质中爆炸。
根据爆炸理论和实际经验可认为影响目标损坏的主要因素是TNT质量、水深、爆炸距离R、方向角α等。本试验固定了其它主要影响因素水平,仅考虑爆炸距离R和方向角α(药包与目标中心连线和目标轴线的夹角,也称爆炸角度)影响因素。实验时在目标内的元件底板上布设一个安装块,在相互垂直的3个方向各安一个加速度传感器,并计算获得3个方向的速度值。为了比较各次试验的毁伤效果,共进行了11次试验,测得目标处的3个加速度峰值和计算得到的3个速度峰值,判别了目标毁伤效果,为分析方便进行归类和编号,试验结果中,有7次目标未发生毁伤,4次目标发生毁伤,如表5。
2 因子分析方法
因子分析法是通过寻找公共因子来综合反映全部指标的大部分信息的统计方法,找出与公共因子载荷较大的原始指标作为特征指标,利用选择的特征指标分析问题其可信度仍然很高。

假定随机向量X满足以下的模型:
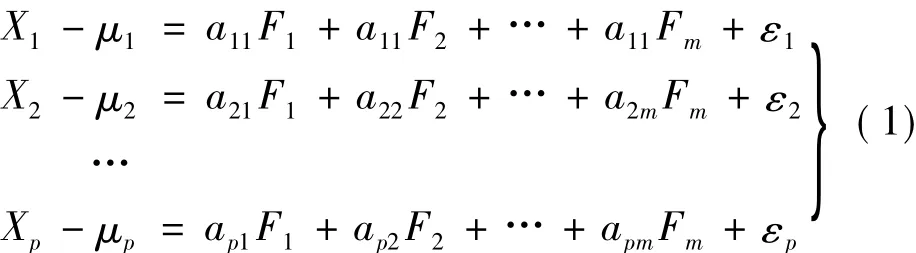
则称模型(1)为正交模型,用矩阵表示为:

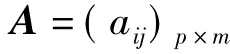
基本步骤:
(1)设x是具有p维(列)向量元素的随机向量。x(1),x(2),…,x(n)是随机向量x的n个样本。将原始数据进行标准化处理,消除量纲的影响。

(2)计算x的相关系数矩阵Cx=E{x'x'T};利用相关函数进行相关性分析。
将每一个指标看做关于n的时间序列值,则第i个指标表示为:xi(n)。利用第i个指标与第j个指标之间的相关函数,可判断两者相关性的强弱。相关函数为:
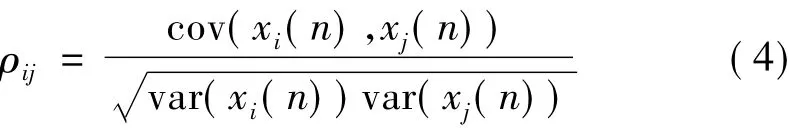
其中,var(xi(n))、var(xj(n))分别是 xi(n)、xj(n)的方差,cov(xi(n),xj(n))是 xi(n)、xj(n)的协方差。
(3) 计算矩阵 Cx的特征值 λ1,λ2,…,λp(λ1≥λ2≥…≥λp),并根据累积贡献率:

确定m取值,找出前m个公共因子。
(4)计算因子载荷矩阵。
(5)对因子载荷矩阵进行旋转变换,得到方差极大正交旋转因子载荷阵。
为了使因子有明显的含义,需对因子载荷矩阵进行正交旋转,则在保持各指标的公因子方差不变的条件下使载荷矩阵通过旋转变换使因子载荷矩阵每一列各元素向0和1两极分化,突出每个公共因子和其载荷较大的原始指标的联系,从而可选择出特征指标。
(6)将因子变为原始指标的线性组合,计算因子值。具体计算步骤见文献[16]。
3 数据处理
3.1 相关性分析
在对目标毁伤效果进行定量分析时,将以实验测得的轴向加速度峰值X1、径向加速度峰值X2、周向加速度峰值X3、轴向速度峰值X4、径向速度峰值X5、周向速度峰值X6六个变量为原始指标进行相关性分析。
利用相关函数对这些指标进行相关性分析,如表1。

表1 六个原始指标之间的相关函数值Tab.1 Correlative function data of character variable among the six primitive indexes
(1)加速度峰值指标之间。径向加速度峰值X2与周向加速度峰值X3线性相关值为0.637 1,有较大的线性正相关。轴向加速度峰值X1与径向加速度峰值X2、周向加速度峰值X3的线性相关值都很小。X1与X2几乎不存在线性相关。
(2)速度峰值指标之间。轴向速度峰值X4与径向速度峰值X5,轴向速度峰值X4与周向速度峰值X6的线性相关值都较大,分别为-0.522 2和-0.600 6,有较大的线性负相关。而轴向速度峰值X4与周向速度峰值X6的线性相关值为0.067 0,不存在线性相关。
(3)各个方向上加速度峰值指标与速度峰值指标之间。轴向加速度峰值X1与轴向速度峰值X4不存在线性相关,径向加速度峰值X2与径向速度峰值X5为较大线性相关,周向加速度峰值X3与轴向速度峰值X6的线性相关值高达0.737 4。
由上面分析可知各个指标间有较强的相关性,说明这些数据之间信息有重叠,为找出影响目标毁伤的主要指标,本文使用因子分析方法选择特征指标。
3.2 特征指标的分析与选择
对数据进行因子分析,前4个因子的累积方差贡献率为96.79%,说明这4个因子已包含了关于原始指标的主要信息,故确定公共因子为 F'1,F'2,F'3,F'4,如表2,得到的因子载荷阵如表3。

表2 公共因子的特征值和贡献率Tab.2 Contributing ratio of public factors

表3 因子载荷阵Tab.3 Factor loading matrix
由于公共因子载荷中出现了相当多的中等载荷,使各个公共因子的含义含糊不清,不利于对因子进行解释。公共因子载荷阵经过方差极大正交旋转以后,所得出的正交因子载荷矩阵如表4所示。在正交因子载荷矩阵中,每个因子对于各个指标的载荷有了明显的差异,对同一个因子而言,载荷向两极分化,中等载荷倾向于消失,这就大大有利于分析解释公共因子和其载荷较大的那些指标的联系,有利于将特征指标提取出来,并且经计算各个指标的共同度都达到92%以上,反映了原始指标对公共因子F的依赖程度高。
(1)公共因子代表了原始指标的大部分信息,所以与公共因子载荷越大的原始指标,包含了目标毁伤的大部分信息。轴向加速度峰值X1与轴向速度峰值X4分别和公共因子F4与F2因子载荷达到了0.992 4和0.941 6。周向加速度峰值X3与径向速度峰值X5分别和公共因子F1与F3的因子载荷达到了0.973 1和0.931 1,由此可知 X1、X3、X4和 X5相对于 X2、X6对目标毁坏的影响更大。
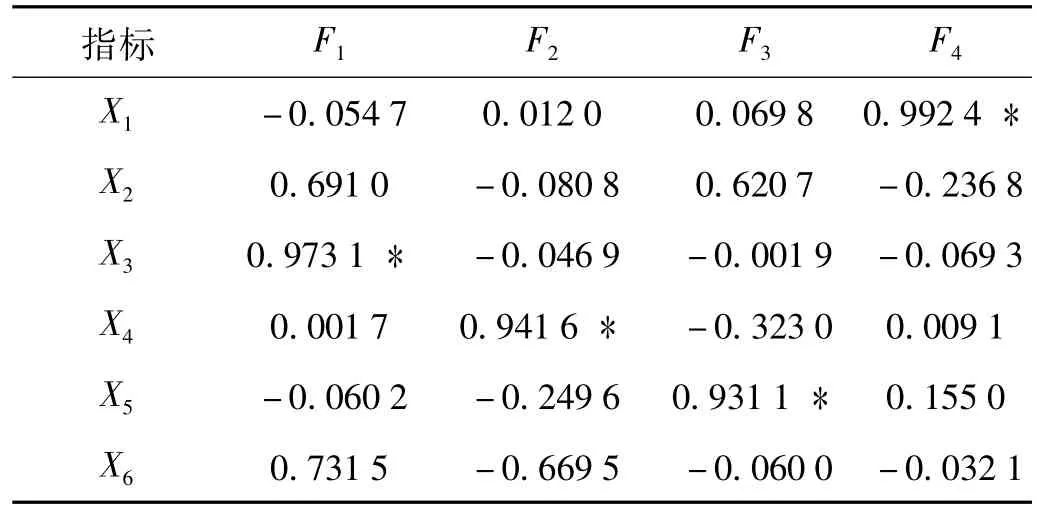
表4 方差极大正交旋转因子载荷阵Tab.4 Factor loading matrix of orthogonal varimax rotation for the data
公共因子的特征量越大代表了方差越大,也即代表了这个公共因子所包含信息越多。公共因子F1比F2,F3,F4的特征值大很多,说明X3所包含的信息最多,而F2相对综合了X4和X6两个指标的信息,F3相对综合了X2和X35两个指标的信息,虽然F4的特征值最小,但它相对只综合了X1的信息,从一定程度上F4比F2与F3更重要。
(2)F2,F3,F4这三个公共因子的特征值相差不大。F1除了代表X3信息外还与X2、X6的载荷很大,而X2与代表X5信息的F3的载荷很大,X6与代表X4信息的F2载荷很大,说明F1在一定程度上反映了F3和F2的信息。并且F4与除X1的其它原始指标的载荷都很小,也即与F1,F2,F3所反映的信息重叠得不多,故选择F1与F4作出得分图1。根据虚线除了第6次试验外能较好的区分目标毁伤类和非毁伤类,而F1与F4主要代表了X3与X1的信息,所以X3与X1相对于X4和X5能更好地表征目标毁伤效果。而且由3.1节的相关性分析知X1与X3几乎不存在线性相关,于是可选择轴向加速度峰值X1与周向加速度峰值X3作为特征指标。
(3)传感器的毁伤模式有很多种,如根部脱掉、底座螺钉松动、联接点断裂是由于轴向方向冲击挤压所造成;而元器件失效、波形产生漂移、电路板移位是由于径向方向振动所造成,可见轴向加速度峰值X1与周向加速度峰值X3这两个指标分别代表了传感器毁伤的两种最重要的毁伤模式。
3.3 判别分析

图1 F1与F4的得分图Fig.1 The scoring figure of F1and F4
为进一步探讨上述用轴向加速度峰值X1与周向加速度峰值X3作为特征指标是否合理,首先选用4个公共因子 F1,F2,F3,F4,利用费歇尔判别法[16-17]对目标毁伤进行判别分析,然后用X1和X3这两个指标进行费歇尔判别分析,如果判别结果大部分相同,就在一定程度上客观地表明X1和X3代表了目标毁伤的大部分信息。
先处理第1组数据,为了判别目标是否毁伤,将峰值向量分为2类:不能使目标毁伤峰值向量和能够使目标毁伤的峰值向量,可以建立水下目标毁伤费歇尔判别模型:

其中 F1,F2,F3,F4由 3.3 节利用因子分析法数据重构而来。根据提出的水下目标毁伤费歇尔判别模型,将11次试验的指标值代入这两个判别函数模型,若W1>0大,则归入未毁伤类;若W1<0大,则归入毁伤类。
同样对第2组也进行费歇尔判别分析得到判别模型:

其中X'1,X'3是X1,X3的标准化数据。再按上面方法进行归类,如表5。
(1)从表5的判断结果可以看出,两个判别模型判断结果都与实际结果一致的有10个,正确率达到90.9%,只有第6号试验的判断结果与实际试验结果不一致。对这个判断出现错误的试验进行分析发现:对于第6号试验,试验结果尽管是传感器未毁伤,但在通电检查中出现误动现象,说明传感器已达到临界毁伤状态。而且这个结果与3.2节中分析的一致。
(2)通过这两组数据判别分析对比结果来看,只利用原始指标X1,X3进行判别分析的结果与用因子分析法重构数据F1,F2,F3,F4进行判别分析的结果一致,这就充分说明了X1,X3包含了目标毁伤的绝大部分信息,选用轴向加速度峰值X1与周向加速度峰值X3作为特征指标是合理的。
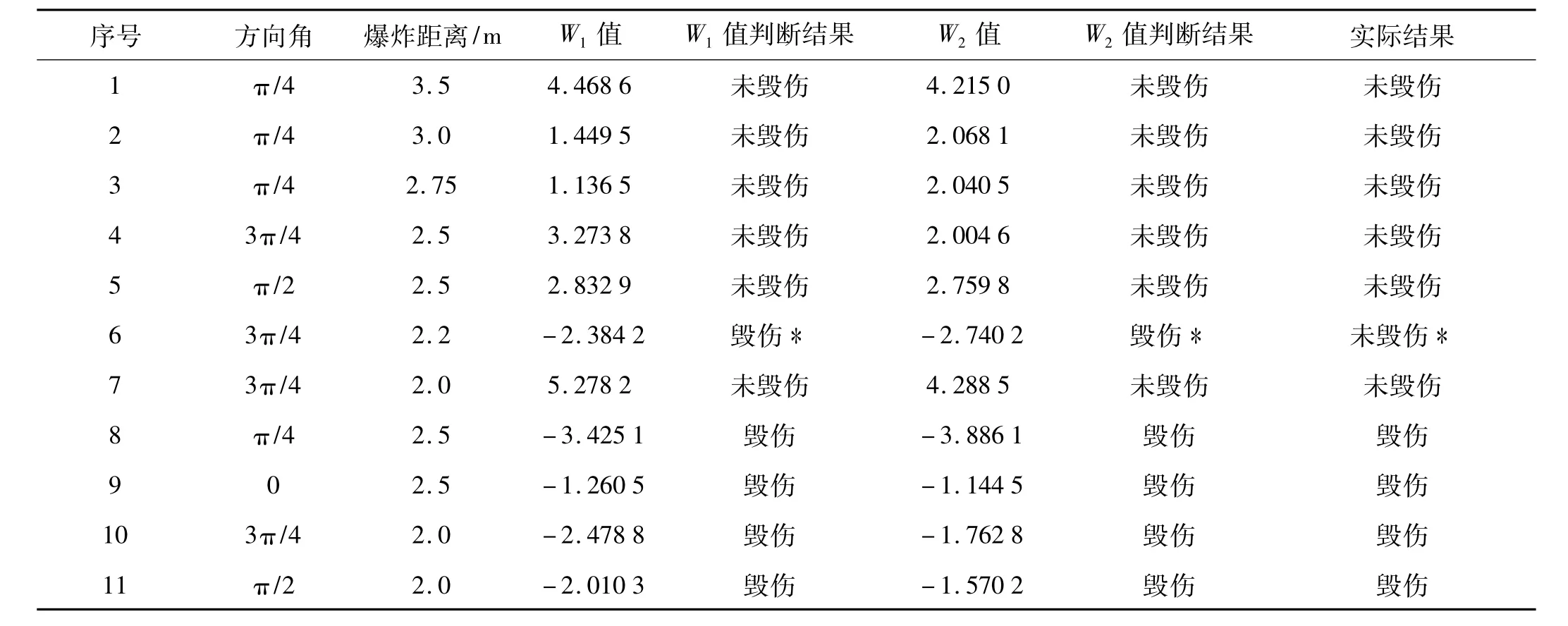
表5 不同方向角和爆炸距离的目标毁伤效果Tab.5 Damage results of the target at different direction angle and explosion distance
4 结论
(1)针对某水下目标传感器毁伤的抗爆炸试验数据,通过用相关函数法对加速度峰值和速度峰值指标进行相关分析,表明这些指标之间相关值很大,在此基础上进一步利用因子分析法,确定了影响水下目标毁伤的特征指标集轴向加速度峰值X1与周向加速度峰值X3,并利用费歇尔判别法证明了选用这两个指标作为特征指标是合理的。
(2)一方面研究者在选择影响水下目标毁伤指标测量时可以只选用这两个指标。另一方面在设计内部传感器时轴向和周向两个方向上时既要由良好的抗冲效果外同时也要有良好的减振效果。
[1]刘建湖.舰船非接触水下爆炸动力学的理论与应用[D].无锡:中国船舶科学研究中心,2002.
[2]刘润泉,白雪飞,朱 锡.舰船单元结构模型水下接触爆炸破口试验研究[J].海军工程大学学报,2001,13(5):41-46.
[3]Cole.Underwater explosions[M].Princeton:Prince-ton University Press,1948.
[4]Hammond L,Grzebieta R.The requirement for hydrostatic initialization in LS-DYNA/USA finite element models[J].Shock and Vibration,2000,7(2):57 -65.
[5]Cho C L,Yuh S T.Shock response of a surface ship subjected to noncontact underwater explosions[J].Int J Impact Engng,2006,33:748 -772.
[6]李 健,荣吉利.水下爆炸圆柱壳塑性动态响应实验及数值计算[J].北京理工大学学报,2008,28(8):659 -662.
[7]黄晓明,朱 锡,牟金磊,等.近距水下爆炸作用下箱型梁模型中垂破坏试验研究[J].振动与冲击,2011,30(2):19-23.
[8]张振华.舰艇结构水下抗爆能力研究[D].武汉:海军工程大学,2004.
[9]牟金磊,朱 锡,黄晓明,等.水下近场非接触爆炸作用下固支方板破口计算[J].振动与冲击,2011,30(1):37-39,55.
[10]姚熊亮,曹 宇,郭 君,等.一种用于水面舰船的水下爆炸冲击因子[J].哈尔滨工程大学学报,2007,28(5):501-509.
[11]姚熊亮,郭 君,曹 宇,等.在水下爆炸冲击波作用下的新型冲击因子[J].中国造船,2008,49(2):52 -60.
[12]姚熊亮,许维军,梁德利.水下爆炸时舰船冲击环境与冲击因子的关系[J].哈尔滨工程大学学报,2004,25(1):6-12.
[13]张志华,钟强晖,李庆民.小药量水下爆炸对水下目标的毁伤有效值评估[J].兵工学报,2009,30(10),1344 -1348.
[14]姚熊亮,杨树涛,张阿漫,等.水下爆炸载荷作用下鱼雷结构优化设计[J].舰船科学技术,2009,31(4):75 -80.
[15]王贡献,褚德英,张 磊,等.舰船设备冲击试验机研究进展[J].振动与冲击,2007,26(2):152 -159.
[16]高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005.
[17]余 颂,陈善雄,余 飞,等.膨胀土判别与分类的Fisher判别分析方法[J].岩土力学,2007,28(3):499-504.
