密肋复合墙板支撑框架结构自振周期计算方法

钱 坤，郭 猛，袁 泉

(1.北京交通大学 土木建筑工程学院，北京 100044；2.吉林建筑工程学院 土木工程学院，长春 130118)

密肋复合墙板支撑框架结构是由框架与其内部嵌入的密肋复合墙板所组成的一种双重抗震结构，属于框架与复合墙板混合承重体系，内部密肋复合墙板是由截面及配筋较小的钢筋混凝土框格，内嵌加气混凝土砌块或其它轻质砌块而成［1－3］。复合墙板嵌入框架内部之后，既可以充当填充墙及隔墙，又对框架起到支撑作用，极大增强了框架结构的整体抗震能力。

由于复合板相对于混凝土墙的抗剪刚度较小，使得剪切变形在结构总水平变形中所占比例较大，在中低层部位甚至超过弯曲变形量［4］，直接影响到结构体系自振周期的计算。自振周期是建筑结构的动力参数之一，是判断建筑结构设计是否合理的重要依据［5］，采用底部剪力法和振型分解法计算结构所受地震作用时需要首先得到结构的基本周期或前若干阶振型对应的周期。工程实践中，可以采用抗弯刚度相等的原则将复合墙板等效为混凝土墙，从而将复合墙板支撑框架结构等效为框架－混凝土剪力墙结构，等效模型法虽然可以用于工程设计，但不能准确反应结构自身特性，中高层复合墙板支撑框架结构设计不宜直接套用框架－剪力墙结构相应公式计算其周期。

本文首先给出复合墙板支撑框架弹性刚度的计算方法，然后采用解析法对结构体系的自振周期计算方法进行研究，为该结构体系的抗震设计提供理论依据。

1 复合墙板支撑框架的弹性刚度

对于砌体填充墙框架的等效抗侧刚度计算方法，国内外学者［6－9］进行了大量试验与理论研究，文献［9］认为框架刚度kf、填充墙刚度kw以及二者之间的连接弹簧刚度ks是决定填充墙框架总刚度的主要因素；我国现行《建筑结构抗震设计规范》［10］对底部框架－抗震墙房屋层间抗侧刚度推荐采用构件刚度叠加的计算方法；对于复合墙板支撑框架，由于其构造形式和力学特性介于填充墙框架与带外框混凝土墙之间，外框架与内部复合墙板呈并联工作状态，本文亦采用构件刚度叠加方法计算复合墙板支撑框架的弹性抗侧刚度。

外框架弹性抗剪刚度采用D值法计算，在文献［4］基础上给出复合墙支撑框架的抗剪刚度为：

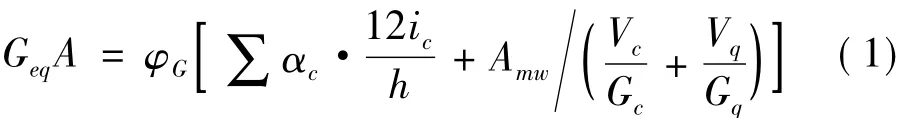
式中：ic为外框架柱的线刚度；h为框架层高；αc为外框架柱侧移刚度修正系数；Amw为复合墙板横截面面积；Gc、Gq分别为复合墙中混凝土和砌块的剪切模量；Vc、Vq分别为混凝土和砌块的体积分数φG为外框架与复合墙相互作用对刚度的影响系数，取φG=1.2。

复合墙支撑框架抗弯刚度采用等效弹性板模型进行计算，计算公式为［11］：

式中：Afc，i为框架柱横截面面积；li为框架柱距外框复合墙形心的距离；X为混凝土肋梁所占墙板的体积比；φE为外框架与复合墙相互作用对刚度的影响系数，取φE=1.0。

2 结构体系自振周期计算

2.1 基本假定

(1)将复合墙支撑框架结构简化为平面模型，如图1所示，即所有分布框架合并为总框架，所有分布复合墙支撑框架合并为总复合墙，连梁按两端铰接考虑［5］；

(2)小变形阶段不考虑密肋复合墙板内部填充砌块以及砌块与混凝土框格粘结界面的开裂，墙体保持线弹性状态；

(3)密肋复合墙框架视为弯剪型悬臂梁，同时产生弯曲变形和剪切变形，普通框架视为剪切型悬臂梁，仅产生剪切变形或以等效抗剪刚度考虑其弯曲变形；

(4)水平连杆为刚性连杆，两端仅传递水平力，结构在楼层处变形协调，且质量、刚度沿高度均匀分布。

图1 计算简图Fig.1 Caculation model

2.2 自由振动方程及自振周期解析解

复合墙板支撑框架结构沿高度方向单位长度质量为m，Cf为总框架的等效抗剪刚度，EeqI、GeqA为总复合墙的抗弯刚度和抗剪刚度。将结构视为无限自由度的连续结构，外框复合墙板视为Timoshenko悬臂梁，基底固定，自由振动状态下的惯性力为－ m∂2y/∂x2，悬臂梁微元体的平衡关系如图2所示。仅考虑截面的剪切变形，忽略转动惯量的影响，则复合墙板支撑框架结构自由振动的运动微分方程组为：

图2 微元体平衡关系Fig.2 Balance relation of the micro unit

式(3)是一个包含双变量即侧向位移y(x，t)和截面转角α(x，t)的微分方程组。令：

代入上式整理得：

再令y(x)=Cesx、a(x)=Desx，其中，C 和D 为任意常数。将y(x)和a(x)代入式(4)和式(5)得：

这是两个包含C、D的齐次代数方程式，由C和D不为零的条件，要求其系数行列式为零，得：

式中：

式(8)的解为 s1= ±iδ，± ε，式中：

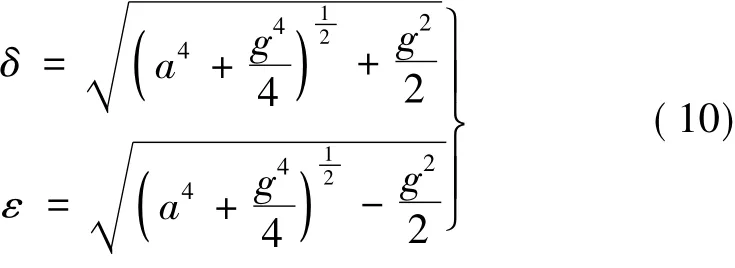
y(x)、a(x)可表示为：

将式(11)、式(12)代入式(8)，由等式两边 sinδx、cosδx、shεx、chεx 的系数各自相等的条件，可得：

由边界条件确定常数：当x=0时，总复合墙支撑框架顶部的弯矩和总剪力为零；当x=H时，复合墙支撑框架底部位移和转角均为零。将式(11)和式(12)代入边界条件，且将D1～D4由式(13)表示为C1～C4，得到包含C1～C4的四个齐次代数方程，由C1～C4不全为零的条件，要求方程组的系数行列式等于零，化简整理得复合墙板支撑框架结构自振方程的特征方程表达式为：

由式(14)和式(15)联立求解得出 λ1、λ2后，即可由式(16)求得复合墙板支撑框架结构的自振频率和周期。

2.3 自振周期近似计算方法

以框架－剪力墙结构自振周期计算方法［5］为依据，建立复合墙板支撑框架结构的振动方程，结合边界条件推导出同时考虑密肋复合墙弯曲变形和剪切变形后基本自振周期的简化计算公式为：

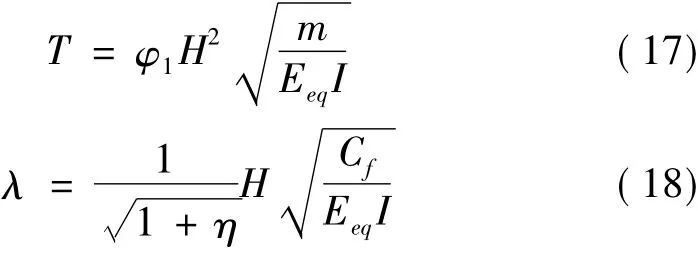
对于任意给定的复合墙板支撑框架结构，GeqA、Cf等参数均为已知，则联立式(18)和式(19)计算λ1、λ2，进而计算出φj和自振周期T；或者可由框架－剪力墙结构的φ－λ曲线查出φj值，这里的λ按式(18)进行计算。

式中各参数意义同前。

3 算例分析

算例1分析密肋复合墙板支撑框架结构抗剪刚度对结构自振周期的影响。

以复合墙板支撑框架结构中密肋复合墙的抗剪刚度为变量，考察不同抗剪刚度对结构自振周期的影响，为从总体上反映自振周期的变化规律，采用符号形式进行表述。结构基本参数为，总密肋复合墙抗弯刚度EeqI，抗剪刚度GeqA，总框架抗剪刚度Cf，三者之间的比例关系如下：

式中：H为结构总高度；b为复合墙的截面宽度；A为复合墙的截面面积；η 为变量。试取 η =3.0、4.0、5.0、6.0依次计算结构的自振周期。

当η=3.0时，将复合墙板支撑框架结构的参数代入式(14)和式(15)，式(14)两边同乘以 H4，式(15)两边同乘以H2，化简得：

以上两式为超越方程，通过试算法求解，将式(21)解出Hλ1后回代至式(20)，计算结果见表1所示，η等于其它值时的计算过程与此相同。分析表1中φ数据可知，剪切变形使得结构自振周期增加，且剪切变形对自振周期的影响随着振型的增加而增大，高振型时，剪切变形的影响不可忽略。

表1 自振周期计算结果Tab.1 Natural vibration period calculation results

算例2在算例1基础上，以η=3.0为例，比较解析法与近似计算方法计算自振周期的误差。

求得 λ1j、λ2j，φj=2π/λ1λ2，T，计算结果见表2 所示。

表2 自振周期计算结果比较Tab.2 Natural vibration period calculation results comparison

由表2计算结果可知，近似计算方法基本自振周期的误差偏小，第一自振周期误差为－1.59%，第二自振周期误差为 －8.97%，第三自振周期误差为－18.85%，计算误差随着振型的增加而增大。

本例中，采用似计算方法计算第一自振周期即基本自振周期的误差不超过5%，可以满足工程计算精度要求，且由于有具体的表格可以查，避免了计算超越方程，采用简化计算方法计算复合墙板支撑框架结构基本周期是可行而且方便的。

4 结论

(1)本文以Timoshenko双变量梁理论及协同工作模型为基础，建立了密肋复合墙板支撑框架结构的频率方程，结合边界条件导出了结构的自振周期计算公式，并给出了基本自振周期的近似计算方法。

(2)算例分析表明：密肋复合墙板支撑框架结构自振周期受复合墙板抗剪刚度影响较大，且影响随着振型的增加而增大，高振型时复合墙板剪切变形的影响不可忽略；采用近似计算方法计算基本自振周期的误差不大，可以满足工程计算精度要求。

(3)本文以密肋复合墙支撑框架结构为例分析弯剪型－剪切型双重抗侧力结构体系的自振周期计算方法，其思路同样适用于其它弯剪型－剪切型双重结构体系自振周期计算。

［1］郭 猛，姚谦峰.框架－密肋复合墙结构新体系研究［J］.地震工程与工程振动，2009，29(5)：73 －78.

［2］ Liu P，Yao Q F.Dynamic reliability of structures：the example of multi－ grid composite walls［J］.Structural Engineering and Mechanics，2010，36(4)：463－479.

［3］黄 炜，张程华，姚谦峰，等.密肋壁板结构弹塑性计算模型研究［J］.振动与冲击，2011，30(2)：233 －237.

［4］郭 猛，姚谦峰.水平荷载下框架－密肋复合墙体的力法位移方程［J］.沈阳建筑大学学报，2010，26(4)：613 －617.

［5］方鄂华，钱稼茹，叶列平.高层建筑结构设计［M］.北京：中国建筑工业出版社，2006.

［6］Chaker A A，Cherifati A.Influence of masonry infill panels on the vibration and stiffness characteristics of RC frame buildings［J］. Earthquake Engineering and Structural Dynamics，1999，28(10)：1061－1065.

［7］Asteris P G.Lateral stiffness of brick masonry infilled plane frames［J］. JournalofStructuralEngineering， 2003，129(8)：1071－1079.

［8］ Ghassan A C，Mohsen L，Steve S.Behavior of masonry infilled nonductile reinforced concrete frames［J］.ACI Structure Journal，2002，136(4)：347 －356.

［9］刘玉姝，李国强.带填充墙钢框架结构抗侧力性能试验及理论研究［J］.建筑结构学报，2005，26(3)：78－84.

［10］建筑结构抗震设计规范(GB50011－2001)［S］.北京：中国建筑工业出版社，2008.

［11］黄 炜.密肋复合墙体抗震性能及设计理论研究［D］.西安：西安建筑科技大学，2004.