基于Pushover方法分析的受腐蚀钢筋混凝土柱抗震性能评价

程 玲，贡金鑫，李 颖

(大连理工大学 土木工程系 结构工程研究所，大连 116024)

由于材料价格低廉，容易成型，钢筋混凝土是当前工程建设中应用最为广泛的结构形式之一，世界各国均是如此。但钢筋混凝土结构仍有许多问题需要解决，主要集中在两个方面，一是钢筋混凝土结构的耐久性问题［1］，二是抗震问题。

钢筋混凝土结构的耐久性与结构所处的环境条件和结构本身的抗腐蚀能力有关，就钢筋腐蚀而言，海洋环境和使用除冰盐的环境受氯离子侵蚀最为严重，有时结构使用不到几年钢筋就发生腐蚀出现顺筋裂缝，影响结构的使用和安全［2］。对于混凝土结构的抗震问题，情况更为复杂，2008年我国发生的汶川地震造成的灾害触目惊心。在我国，很多钢筋混凝土结构处于地震的多发地带，同时又处于严重的腐蚀环境中，所以钢筋混凝土结构受腐蚀后的抗震性能是需要研究的重要课题。本文在文献［3］试验研究的基础上，采用Pushover方法研究了地震作用下受腐蚀钢筋混凝土的变形。

1 受腐蚀偏心受压构件的荷载－变形曲线和滞回特性

在自然环境和使用环境中，在受腐蚀介质的影响下，钢筋混凝土构件会受到不同程度的腐蚀，抗震性能降低。文献［3］对8组16个锈蚀率为0% ～19.8%的电化学锈蚀的钢筋混凝土偏心受压试件进行了低周反复荷载试验，结果表明，试件的抗震性能与钢筋锈蚀率有关。腐蚀作用导致钢筋截面面积减小，锈蚀产物的膨胀使混凝土保护层产生顺筋裂缝，钢筋与混凝土间的粘结性能减弱，钢筋滑移增大，构件强度和刚度均降低［4］。随着锈蚀量的增加，试件的屈服荷载、屈服位移、极限荷载和极限位移都显著降低。从荷载－变形曲线看，钢筋未锈蚀的构件达到屈服荷载后有较长的延伸段；对于钢筋锈蚀的构件，随着锈蚀率的增大，延伸段逐渐缩短，延性降低。从滞回曲线看，钢筋未锈蚀构件的滞回环比较丰满，构件破坏时需要消耗较多的能量，随着锈蚀率的增大，滞回环变窄，甚至只承受几个荷载循环，构件就发生破坏。

1.1 荷载－变形曲线

文献［5］研究了受腐蚀钢筋混凝土偏心受压构件的恢复力模型。研究表明，受腐蚀钢筋混凝土偏心受压构件的恢复力模型仍可采用与未腐蚀构件相似的规则，但需考虑受腐蚀构件滑移增大对荷载－变形曲线的影响。经过对试验结果的分析，提出下面受腐蚀偏心受压构件荷载－变形曲线的公式：

式中：fcorro为受腐蚀钢筋混凝土构件的变形；f为未腐蚀钢筋混凝土构件的变形；fyy为按式(2)考虑钢筋锈蚀后面积减少、钢筋屈服时构件的变形；ρ为钢筋腐蚀率。式(1)可用作受腐蚀构件恢复力模型的骨架线。

未腐蚀钢筋混凝土构件(见图1)的变形f按下式计算：

式中：φ为构件根部截面的曲率；φy为构件的屈服曲率，与屈服荷载相对应；H为构件高度，如图1所示；lp为塑性铰长度，塑性铰长度的计算有多种，本文采用如下计算公式［6］：

图1 构件曲率沿高度的分布Fig.1 Curvature distribution along the height

在水平力P和轴力N作用下，构件根部截面的弯矩为M=PH，如图1所示，根部截面受压混凝土边缘纤维的应变为εmax，混凝土受压区高度为xc，则根部截面曲率由下式计算：

其中：受腐蚀钢筋的面积为Ascorro=A'scorro=As(1－ρ)，As为钢筋未腐蚀时的面积。

按上面公式计算荷载－变形曲线的步骤如下：

① 选定混凝土和钢筋的应变－应变关系；② 给定P，得到M=PH，由式(5)和式(6)联立求得 εmax和xc；③由式(4)计算 φ；④由式(2)计算 f；⑤由式(1)计算fcorro，进而得到P－fcorro曲线

图2 构件截面应变、应力分布Fig.2 Stress strain distribution

1.2 滞回特性

在低周反复荷载作用下，钢筋混凝土构件滞回曲线的面积反映了构件的非线性耗能能力。文献［3］将构件的平均耗能系数定义为：

式中：Q为构件破坏前消耗的总能量(所有滞回环的总面积)；m为滞回环数目；Ey为钢筋的弹性模量。平均耗能系数反映了一个滞回环的平均相对耗能。根据文献［3］的试验结果，得到腐蚀构件与未腐蚀构件平均耗能系数之比随钢筋锈蚀率的关系如图3所示。根据图3，与未腐蚀的构件相比，腐蚀构件一个滞回过程消耗的能量随锈蚀率呈线性规律降低，用下式表示：

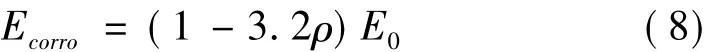
式中：Ecorro为腐蚀构件一个滞回环的耗能；E0为未腐蚀构件一个滞回环的耗能。

图3 平均耗能系数与锈蚀率的关系Fig.3 Relation between average dissipative coefficient and corrosion rate

2 Pushover方法

Pushover方法是近年来在国外得到广泛应用的一种结构抗震能力分析方法，可估计结构在罕遇地震作用下的弹塑性变形，从而对结构在地震作用下的变形能力进行评估。目前，Pushover方法已被国外的很多标准和规范采用，如 ATC －40［7］、欧洲规范 EN 1998－1∶2005［8］。进行 Pushover分析首先要通过对结构进行推覆确定荷载－变形曲线，根据性能点对应的割线刚度和等效阻尼，采用能力谱和位移需求谱确定目标位移。本文选单自由度结构体系分析偏心受压构件腐蚀后的地震反应，所以下面的分析方法和步骤也是针对单自由度体系的。

2.1 割线刚度和等效阻尼比

用Pushover方法分析结构的地震反应时，如果结构进入塑性阶段，则采用结构的割线刚度。割线刚度按下式计算：

其中：Δd为结构的水平位移，Fd为与 Δd对应的水平力。

如果将结构等效为弹性体系，则根据割线刚度计算结构的基本周期

其中：M为单自由体系的质量。

图4为结构的荷载－变形曲线，Y为屈服点，可取为构件第一根钢筋屈服时的点［9］。假定A为荷载－变形曲线上水平位移对应于Δd的点，用折线OYA代替结构的荷载－变形曲线，则由图4可得：

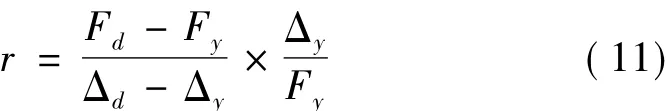
图4 结构割线刚度Fig.4 Structural secant stiffness

Pushover分析采用的等效阻尼比为结构本身的粘滞阻尼比与等效滞回耗能阻尼比的和。根据文献［10］

的公式并考虑式(8)表示的腐蚀构件一个滞回环耗能与未腐蚀构件一个滞回环耗能的关系，得腐蚀构件的等效阻尼比：

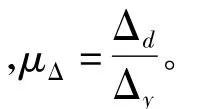
2.2 位移反应谱

式(12)为受腐蚀结构振动一个周期内滞回耗能等效为粘滞阻尼耗能后得到的阻尼比公式，利用等效阻尼比可将结构的弹性反应谱转化为弹塑性反应谱。

设弹性加速度反应谱为SA，结构弹性位移与弹性加速度的关系为：

式中：T为结构的基本周期。

采用《公路桥梁抗震设计细则》［6］的反应谱进行分析。将规范的加速度反应谱SA代入式(13)得到位移反应谱：

式中：Smax为水平加速度反应谱最大值，按下式计算：

式中：Ci为抗震重要性系数；Cs为场地系数；A为水平向设计基本地震加速度；Cd为阻尼调整系数，按下式计算：

式中：ξ为结构阻尼比，本文Pushover分析中取式(12)表示的 ξeff。

2.3 计算步骤

根据上面的公式，按下列步骤进行Pushover分析：

① 确定结构的荷载－变形曲线，求出结构屈服位移Δy；② 假定目标位移Δd，求得位移延性系数μΔ，并确定对应的水平力Fd；③ 计算结构等效阻尼比ξeff；④计算割线刚度Ke，确定周期Td；⑤ 按式(13)计算位移Sd；⑥ 将Δd与Sd比较，如果误差满足规定的要求，则所得Δd即为结构在该规定地震下的最大变形，否则转②重新假定Δd进行计算。

3 受腐蚀钢筋混凝土构件的变形分析

下面通过一个具体例子说明腐蚀对钢筋混凝土偏心受压构件抗震变形能力的影响。

某钢筋混凝土单排墩桥梁处于海洋环境，按《公路桥梁抗震设计细则》(JTG/T B02－01－2008)，抗震设防标准属于C类。墩柱长9 m，柱截面尺寸1 200 mm×1 200 mm，集中于每个墩柱的平均质量为80 t，桥梁所处场地类别为Ⅲ类。柱混凝土采用C40，抗压强度标准值 fc=26.8 N/mm2，柱内对称布置 12φ30HRB335 钢筋，钢筋屈服强度标准值为fy=335 N/mm2，极限强度为fu=380 N/mm2，弹性模量为200 GPa。采用文献［11］的混凝土和钢筋应力－应变关系。分析模型如图5所示。

按本文的分析步骤对本例进行计算，得到柱不同锈蚀率下的荷载－变形曲线P－fcorro如图6所示。由图可以看出，钢筋屈服后曲线有一个平台，之后曲线又向上扬起，扬起是由钢筋硬化引起的。

图7示出了柱的屈服位移、屈服荷载、极限位移和极限荷载随钢筋锈蚀率的变化。从图中可以看出，随着钢筋锈蚀率的增加，墩柱的屈服位移、屈服荷载、极限位移和极限荷载均降低。屈服荷载和极限荷载的降低基本呈线性，而屈服位移和极限位移的降低呈非线性。

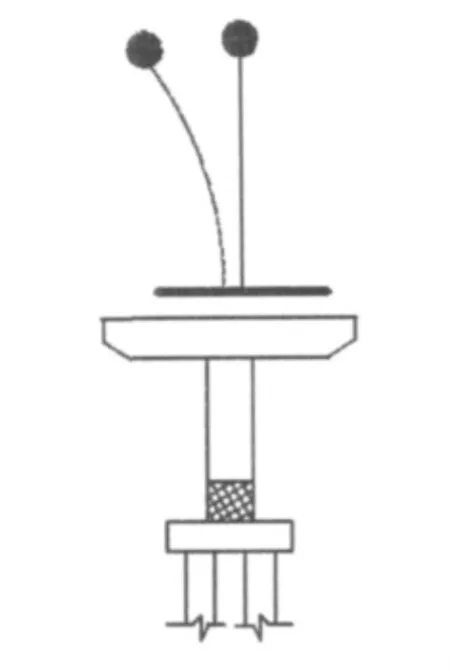
图5 桥梁抗震分析模型Fig.5 Seismic model of bridge

图6 墩柱的P－fcorro曲线Fig.6 P － fcorrocurve of pier

分别按设防烈度7度、8度和9度进行地震反应分析，考虑E2地震作用，结构重要性系数Ci=1.0。对于Ⅲ类场地，特征周期为0.65 s。7度时，场地系数Cs=1.3，水平向最大加速度 A=0.1 g，其中 g=9.8 m/s2；8度时，Cs=1.2，A=0.2 g；9 度时，Cs=1.0，A=0.4 g。

按照本文前面的步骤对桥梁进行Pushover分析，得到不同地震烈度下结构的变形与锈蚀率的关系如图8所示。由图可以看出，对于不同的地震烈度，随钢筋锈蚀率的增加，结构变形增大；地震烈度越大，变形随钢筋锈蚀率增加的越快。所以，在同一钢筋腐蚀率下，地震越强，结构反应增加得越明显。

如果地震作用下可接受的结构变形标准不变，可按上述方法计算结构不同锈蚀率时能够经受的地震作用。假定结构变形为45 mm，在锈蚀率为0%、10%、20%和30%时，结构能够承受的变形如表所示，其中的抗震设防烈度是根据水平地震影响系数通过内插计算得到的，图9给出了相应的图示。由表和图可以看出，随着结构钢筋锈蚀率的增加，在相同的变形条件下，相同场地上结构可承受的地震作用降低，说明了锈蚀对结构抗震能力的不利影响。如果将变形分别提高到60 mm和75 mm，表1给出了相应的计算结果。

图7 荷载、位移随钢筋锈蚀率的变化Fig.7 Changes of load and displacement

表1 结构变形为45mm、60mm和75mm时不同锈蚀率的结构可承受的地震作用Tab.1 The earthquakes being endured by the structure with different corrosion rates when the deformation of structures are 45 mm，60 mm and 75 mm

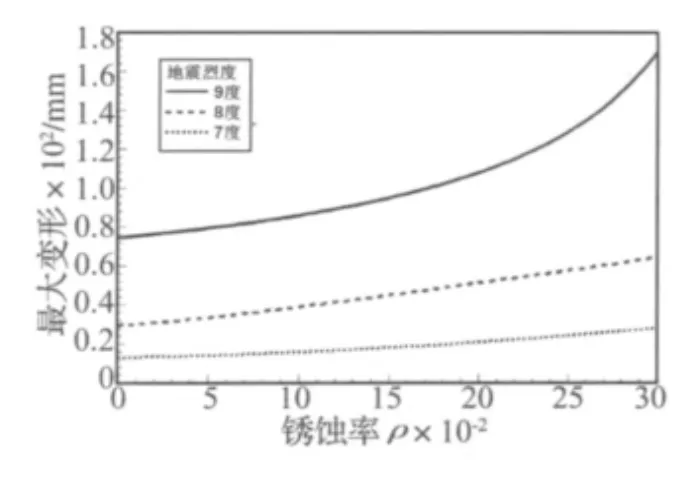
图8 最大变形与锈蚀率的关系Fig.8 Relation between maximum deformation and corrosion rate

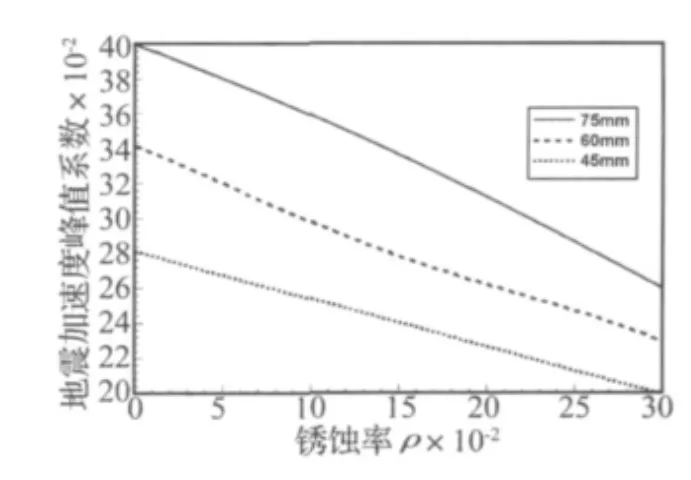
图9(a) 峰值加速度系数与锈蚀率关系曲线Fig.9(a)Relation between peak acceleration coefficient and corrosion rate

图9(b) 地震烈度与锈蚀率关系曲线Fig.9(b)Relation between seismic intensity and corrosion rate

4 结论

本文采用Pushover方法分析了不同锈蚀率下钢筋混凝土结构的地震反应。结果表明：

(1)随着锈蚀率的增大，相同地震作用下结构的变形增大；

(2)在相同变形要求下，结构可经受的地震作用随钢筋锈蚀率的增加而降低；

(3)随着钢筋锈蚀率的增加，构件的屈服荷载及对应的屈服位移，极限荷载及对应的极限位移均减小，屈服荷载和极限荷载的呈线性降低趋势，而屈服位移和极限位移呈非线性降低趋势。说明钢筋锈蚀对构件变形的不利影响很明显。

［1］金伟良，赵羽习.混凝土结构耐久性［M］.北京：科学出版社，2002.

［2］洪定海.混凝土中钢筋的锈蚀与保护［J］.北京：中国铁道出版社，1998.

［3］贡金鑫，仲伟秋，赵国藩.受腐蚀钢筋混凝土偏心受压构件低周反复性能的试验研究［J］.建筑结构学报，2004，25(5)：92 －104.

［4］何世钦，贡金鑫.钢筋混凝土梁中锈蚀钢筋粘结性能的试验研究［J］.哈尔滨工业大学报，2006，38(12)：2167－2170.

［5］贡金鑫，李金波，赵国藩.受腐蚀钢筋混凝土构件的恢复力模型［J］.土木工程学报，2005，38(11)：33 －44.

［6］JTG/T B02－01－2008.公路桥梁抗震设计细则［S］.2008，10.

［7］ATC，Seismic evaluation and retrofit of concrete buildings［S］.Vol.1，ATC － 40，Applied Technology Council，Redwood City，1996.

［8］ Design Provisions for earthquake resistance［S］.European Committee for Standardization Eurocode8，2004.

［9］ Ferrito J，Dickenson S，Pricestlty N，et al.Seismic criteria for california marine oil terminal［S］.Naval Facilities Enginieering Service Center，1999.

［10］ Takeda T，Sozen M A，Nielsen N N.Reinforced concrete response to simulated earthquake［J］.J.Struct.Div.ASCE，1970，96(12)：2557 －2573.

［11］混凝土结构设计规范［S］.GB5001－2001.