粘性液体对管道中扭转导波传播特性的影响研究

孔维梁，周 丽， Fuh-Gwo Yuan

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016;2.Department of Mechanical and Aerospace Engineering，North Carolina State University，Raleigh，NC 27695，U.S.A)

管道的腐蚀老化是工业中的一个重要问题，而超声导波是一种很有效的损伤检测工具。管道大多含有液体，或者浸泡在液体中，需要研究与液体相接触的管道中波的传播特性。

许多学者对带有液体的圆柱/管中的波传播进行了研究。Nagy等［1］把粘性液体假设为特殊的固体，理论分析了纵向导波在浸粘性液体里纤维中的传播。Barshinger等［2］对带粘弹性包覆层管道中波的传播特性进行了理论和实验研究。Elvira-Segura［3］在 Grosso理论的基础上分析了内部有粘性液体的管道中波的纵向模态，讨论了频率、管厚度和液体粘性对速度和衰减的影响。Aristegui等［4］在 Nagy 等［1］的理论基础上，研究了管内外为液体的情况下导波的传播特性，并有实验比较。Bllandras等［5］研究了导波在液体和固体半空间边界上的衰减现象。

在以上研究中所关注的是导波的纵向模态。纵向模态对于管道周向的缺陷较敏感，但对轴向缺陷不太敏感，而理论上扭转模态对于这两种损伤都敏感。刘增华等［6］对超声导波扭转模态在粘弹性包覆层管道中的传播特性进行了研究。他得安［7］等对充粘液管材超声纵向导波的无损检测参数进行了探讨。Viens等［8］研究了埋藏在无限大固体中杆的扭转波传播特性，并将液体假设为横波速度很小的固体，得到了浸在液体中圆杆的扭转波的相速度和衰减，但没有实验验证。Kwun等［9］通过实验研究了埋在煤、沥青等介质中的管道T(0，1)模态的衰减特性，发现衰减随频率升高而增加。

本文研究了接触粘性液体的管道中扭转导波的传播特性。推导了管壁附近粘性液体的剪切运动，计算并分析其对波传播的影响;其中主要讨论了粘性，密度等对T(0，1)模态的衰减影响和液体分别处于管的内外时波的衰减，以对扭转导波在管道损伤检测中的应用提供一定理论依据。

1 扭转波运动理论

1.1 扭转波在各向同性管道中的运动

由文献［11－12］，在一个各向同性、均匀、弹性的无限长圆管中(如图1)，假设一个时间简谐波沿着管道传播，管中扭转波的位移与剪切力分别为uθ和τrθ有如下表示:

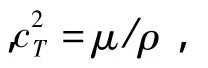
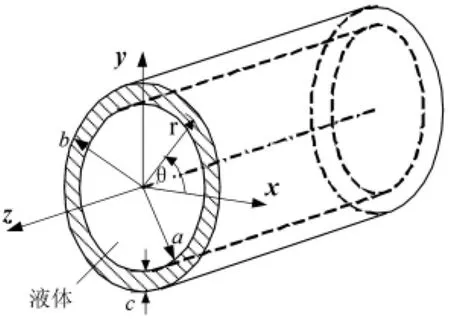
图1 粘性液体充满管道内部Fig.1 An infinite long pipe filled with viscous liquid

1.2 剪切波在液体中的运动

管的扭转波是剪切波，只有θ方向的运动。只有粘性液体可以对剪切波产生影响。假设液体为牛顿流体，忽略体力的作用，液体初始为静止。在这个问题中管壁平行于轴线运动，对液体产生纯剪切力。由于典型损伤检测使用的导波持续时间很短(10－4s)，波包包含的波峰数量少，管壁的振动幅度小，认为液体还是层流流动。由固壁无滑移条件，靠近固壁的液体运动形式与管壁一致即做间谐运动。在动量方程中忽略体力和压缩性，简谐波在液体中传播时速度的表示为［3］:

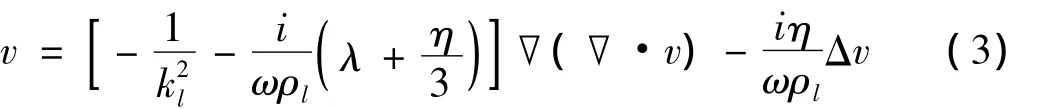
式中:λ和η分别表示膨胀和剪切粘性系数，ρl为液体静止时的密度，v为速度矢量。对速度进行Helmholtz分解:v=▽φ+▽×Ψ。其中φ为压缩标量势，Ψ为等体积矢量势。它们都为简谐运动的形式:

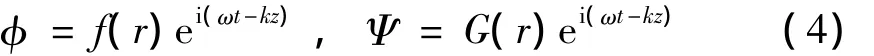
解关于矢量势Ψ的方程，可以得到液体中的速度和剪切力:

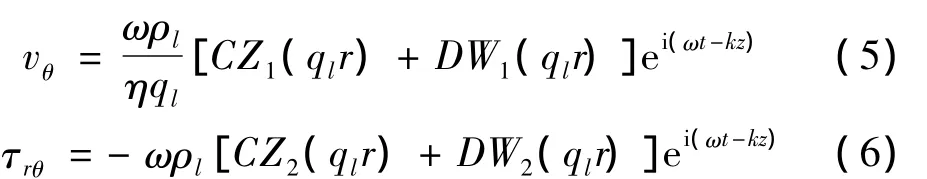
当扭转波传过时，由管壁产生的扰动将在液体中传播并不断衰减。扰动是否能从另一侧管壁反射将直接影响波的形式。这里使用边界层理论加以分析。为确定波运动的性质，我们用边界层的厚度量级进行波影响范围的估计。厚度估计如下式［10］:

其中L为运动的特征尺度，在这里取为管壁振动的振幅;U为特征速度，取为管壁质点振动的平均速度;δ为边界层的厚度;f为运动频率。振动周期为:T=1/f=2L/U。则边界层厚度的量级为:

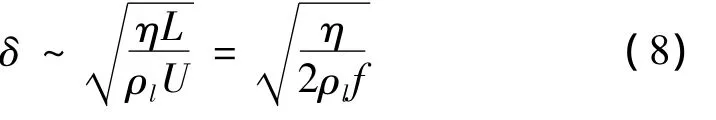
为估计边界层厚度的大小，取较大粘性系数和较小的液体密度、频率代入式子。取粘性系数η=1 Pa·s，密度为ρ=1 000 kg/m3，频率为f=1 kHz时，可以得到边界层厚度δ～7.07×10－4m，为10－3m量级。这个量级远小于一般使用的管道，也小于本文例子的半径a=0.1 m，δ≪a。

2 边界条件与频散方程

2.1 液体在管道内

如图1，管的内径为a，外径为b，壁厚为c，管内部有粘性液体。在管的边界上力和位移连续:内表面上的应力应等于液体对管的剪切力，位移和速度等于液体运动的位移和速度;管外部为自由，应力为零、

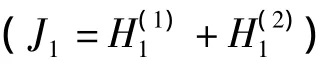
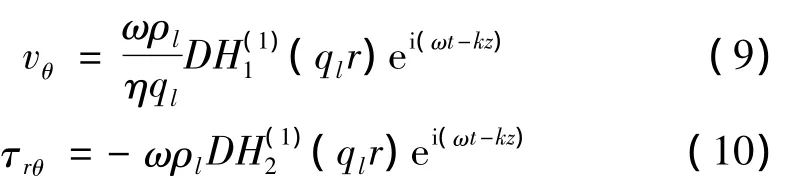
式(1)，式(2)中 Bessel函数的选择见文献［11］，在变量q为复数时Bessel函数的选择应和q为实数时一致。把式(1)，式(2)，式(9)，式(10)代入边界条件并联立，令矩阵方程的行列式为零，由此可以得到频散方程，简化后的频散方程为:

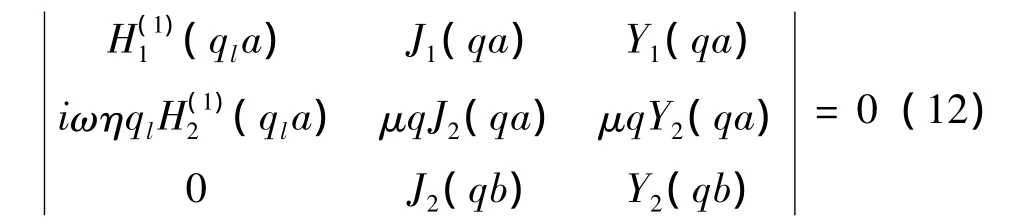
2.2 液体在管道外

当管外面有粘性液体而内部自由，其他参数同前节。此时液体中的波只向外行，液体中的速度和剪切力将由第二类Hankel函数表示。类似式(15)，将位移和应力式子代入边界条件中可得频散方程:

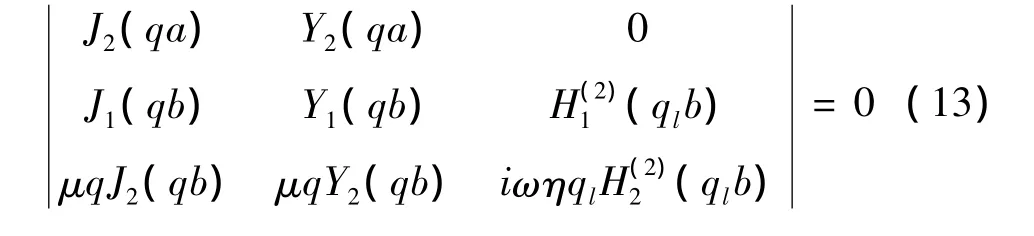
3 带粘液管中扭转波的位移模式和传播特性

解出频散方程在不同频率下的根，可以得到频散和衰减曲线:由实波数得到相速度，由虚波数得到波的衰减。由于粘性液体波的衰减总是存在，波数为复数。在解频散方程时使用了Muller法迭代寻根。数值求解复数根需要在实部和虚部两个坐标轴进行搜索，但是在此处当频率接近零时，各阶模态波数的实部都很接近于零，而虚部差别很大。利用这个性质，计算时可以只在虚轴上搜索。求得波数后可以给出波的频散和衰减曲线，在本文中定义如下:

相速度:

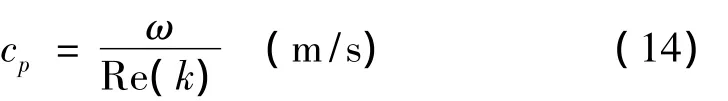
正交化衰减:

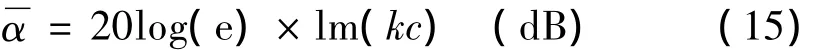
其中圆频率 ω =2πf，f为频率。

3.1 扭转波的频散特性

管道为内径 a=0.1 m，外径为 b=0.11 m，厚度c=0.01 m的铝管。管道材料和液体的具体数据见表1。

当管道与粘性液体接触，液体会被管道的运动带动，同时管中的能量将散失到液体中去，所以波会出现衰减，同时也会存在频散。图2、图4和边界自由管的相速度速度频散曲线非常相似，明显的区别是T(0，1)模态出现了小的频散，这个现象是由粘性液体造成。由图3可以看到这六阶扭转模态都有不同程度的衰减，衰减的值随频率的增大而增大。同样频率下T(0，1)模态的衰减小于其他阶。除T(0，1)模态外，较低阶扭转模态波的衰减随频率的增长速度大于更高阶模态。当频率增加时，除T(0，1)模态波之外的波的衰减将会接近。

表1 管道和液体的属性Tab.1 The material properties of the pipe and liquid

当粘性液体在管道的外部时，图4、图5显示了和图2、图3类似的现象，只有衰减曲线有明显不同。比较图3和图5，虽然衰减都是随频率增加而增加的，曲线形状也很相似，但T(0，1)模态的衰减有明显差别:液体分别在管内和管外时的衰减之比约为3/4。更高阶模态的衰减则差别不大。

3.2 与文献中实验结果的比较

在文献［13］中有实验如下，实验对象是一根浸在甘油中的铁杆，杆的半径为1 mm，材料常数如表2。实验测量了杆中T(0，1)模态的衰减。在图中衰减的单位是1/m(或者np/m)。

表2 文献［11］中实验材料的性质Tab.1 The material properties in the pape［11］

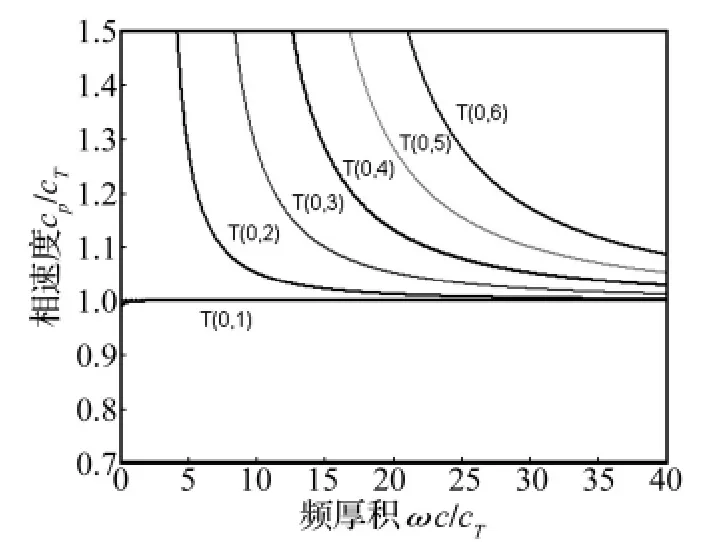
图2 管内有液体时前六阶扭转模态的相速度曲线(η=1 Pa·s)Fig.2 The normalized phase velocity of first six modes of torsional wave in a pipe filled with liquid(η =1 Pa·s)

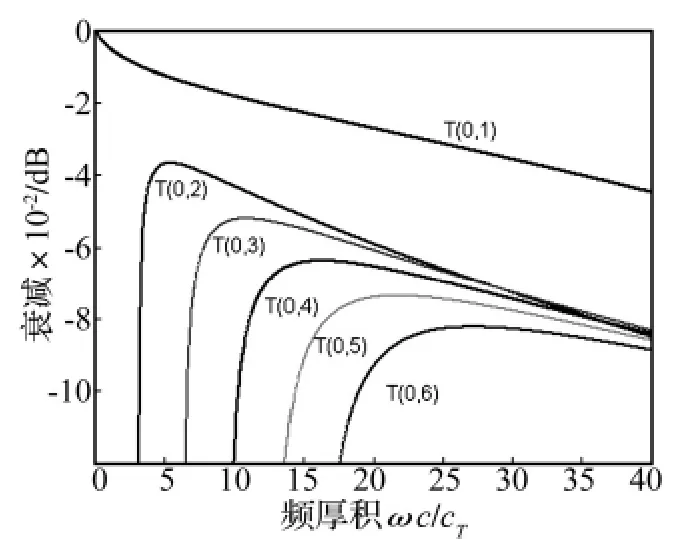
图3 管内有液体时前六阶扭转模态的衰减曲线(η=1 Pa·s)Fig.3 The normalized attenuation of first six modes of torsional wave in a pipe filled with liquid(η =1 Pa·s)

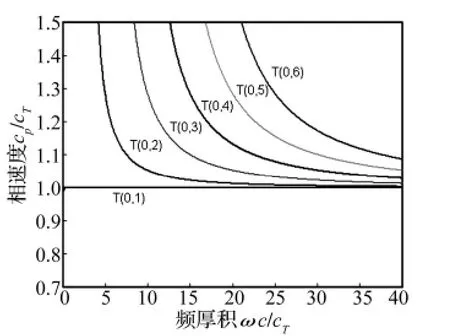
图4 管外有液体时前六阶扭转模态的相速度曲线(η=1 Pa·s)Fig.4 The normalized phase velocity of first six modes of torsional wave in a pipe immersed in liquid(η =1 Pa·s)

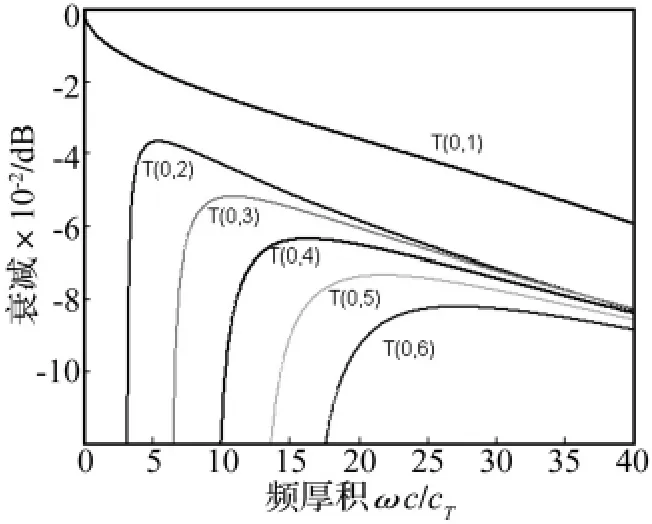
图5 管外有液体时前六阶扭转模态的衰减曲线(η=1 Pa·s)Fig.5 The normalized attenuation of first six modes of torsional wave in a pipe immersed in liquid(η =1 Pa·s)

可以看到本文计算结果与该实验结果符合较好。文献［14］中也有类似实验，因结果相似不再列出。但是在这两篇文献中研究的是细铁杆，并未讨论液体在管内部的情况，但目前还缺乏管内有粘液时的实验结果。

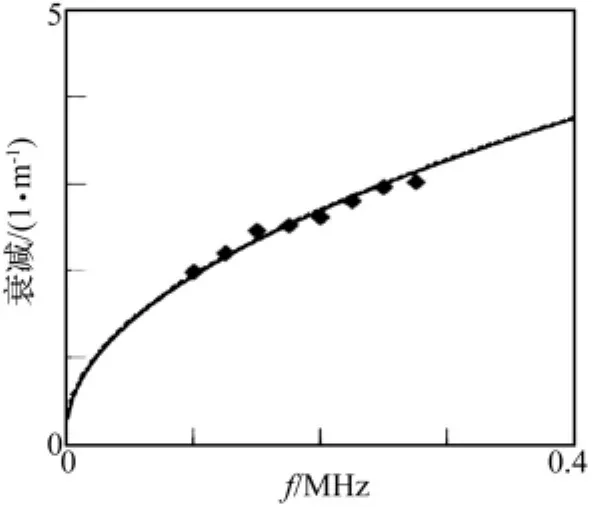
图6 理论计算结果和文献实验结果的对比(实线为理论结果，点为实验结果)Fig.6 Comparing of the results of theoretical calculations and experimental(solid line is the theoretical results，point to experimental results)

3.3 扭转波的位移模式

图7为内部有粘液的管道的扭转波沿管壁厚方向上周向位移的分布曲线，频率为300 kHz。此处的位移为归一化后的(uθ(r)/(uθmax－ uθmin)。这里只列出了前四阶扭转波的位移沿壁厚的分布。由图7可知，T(0，1)模态中管的位移都是同一方向的，而更高阶模态的位移在两个方向上都有分布，阶数越高位移曲线通过零点的次数越多。位移分布曲线的零点说明该点没有运动，用导波进行损伤检测的时候，此处的损伤有可能检测不到，或是检测能力降低。从这个意义上来说位移分布上没有零点将是最好的。由图2，图4可知T(0，1)模态的频散很小，且没有截止频率。所以相对于其他阶模态，T(0，1)模态的优势是很明显的。下面将重点讨论粘性对T(0，1)模态的影响。

图8是管内充满粘性液体时T(0，1)模态位移的分布，图中显示的半径范围是0.09 m～0.11 m，图的左边为液体，右边为管道。由图8(a)为频率1 kHz的位移分布。图8(b)中频率增大到10 kHz，其位移分布与图8(a)相比有相同趋势，而液体的位移在管壁附近衰减更快，波在液体中的影响范围更小(约0.002 m)。这些都和前文假设相符，边界层厚度的量级也一致，证明了此假设的正确性。在图8中，管壁中位移的分布和半径成正比，管内壁与外壁位移之比为10∶11。这和自由边界管中T(0，1)模态的位移分布相同，说明此时粘性液体对管中导波的改变并不大。

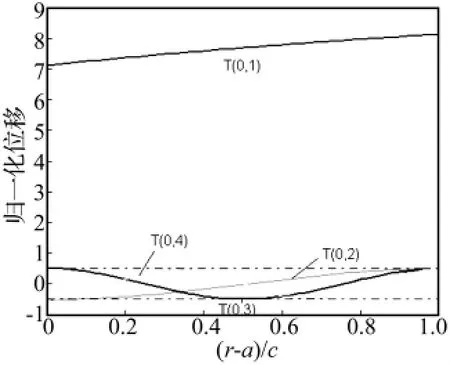
图7 管内有粘液时扭转模态的位移沿管壁分布，频率为300 kHz，粘性系数为1 Pa·sFig.7 The displacement distribution of the torsional wave of a pipe filled with liquid，f=300 kHz，η =1 Pa·s

4 液体粘性和密度对T(0，1)模态的影响

4.1 液体粘性对各向同性管中T(0，1)模态的影响

扭转模态在表面上只有θ方向的剪切运动，T(0，1)模态的衰减完全是由于剪切力，它理论上应该对周围介质的剪切性质比较敏感。从式(8)中可知，频率越高粘性液体中的剪切力越大，也就是说衰减应随频率增大而增大。

由图9，液体的粘性会对波的相速度频散特性造成影响，当液体在管外侧时频散更大，但相速度改变值都很小。尽管粘性系数从0.01增加到10，但速度的变化只有近1/1 000，约几m/s，这在实际操作中难以测量。粘性对波传播的干扰主要体现在衰减上。从图10可以很明显的看到衰减随粘性增大单调增加，衰减大小和粘性增加的关系并不是线性的。衰减也随着频率增大而增大，在频率低时衰减与频率的曲线类似抛物线。而在频率和粘性较大时曲线就改变了，其斜率变的更大。当液体在管外时衰减比液体在管内时的情况大。

图11是频率固定时液体粘性与T(0，1)模态衰减的关系曲线。据比较这两条曲线近似为抛物线，而且液体分别在管内和管外时其衰减之比约为3/4。

图8 管内有粘液时T(0，1)模态的位移分布，粘性系数为1 Pa·sFig.8 The displacement distribution of the the first torsional wave mode filled with liquid，η =1 Pa·s

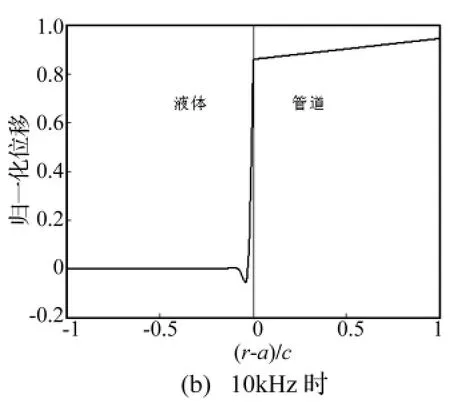
图9 在不同液体粘性系数时T(0，1)模态的相速度曲线Fig.9 The normalized phase velocity of the first torsional wave mode with liquid of different viscosity

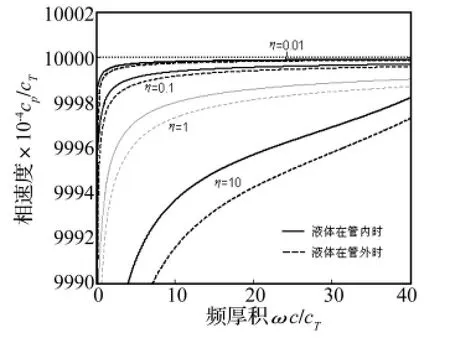
图10 在不同液体粘性系数时T(0，1)模态的衰减曲线Fig.10 the normalized attenuation of the first torsional wave mode with liquid of different viscosity

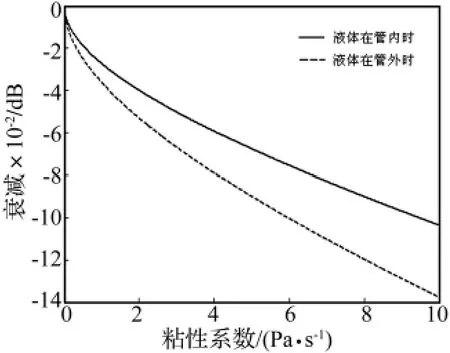
图11 当频率为1 MHz时液体粘性与T(0，1)模态衰减的关系Fig.11 The relation between attenuation and dynamic viscosity coefficient of the first torsional wave mode，f=1 MHz

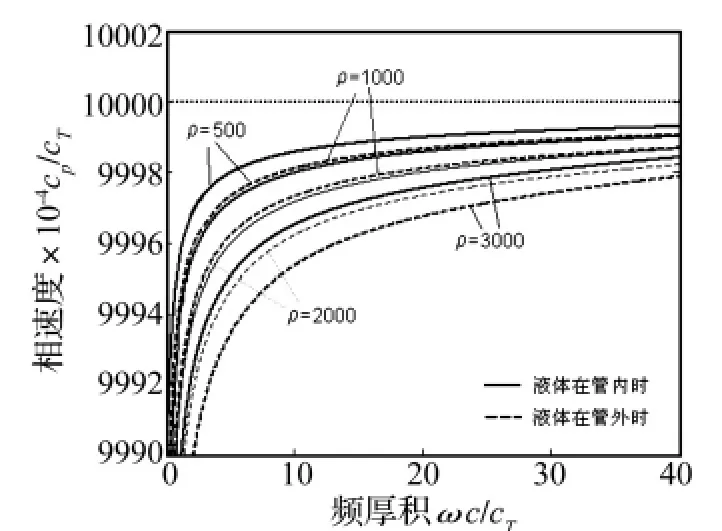
图12 液体在不同密度时T(0，1)模态的相速度曲线，密度单位为kg/m3，粘性系数为1 Pa·sFig.12 The normalized phase velocity of the first torsional wave mode with different liquid density，the unit of density is kg/m3

4.2 液体的密度对T(0，1)模态衰减的影响

由图12可知，液体的密度改变对T(0，1)模态的相速度影响也很小。但是密度的改变对曲线的形状改变不多。由图13，T(0，1)模态的衰减随液体密度的变化比较平缓。在密度小的时候衰减随密度上升较快，而后逐渐放慢。同样液体在管外时产生的影响比液体在管内时更大。由图14可以看到密度与衰减的变化关系，与密度和衰减的关系一样，其中的曲线也是近似为抛物线，即是说衰减的平方近似与密度成正比。这个结论在图12，图13的频厚积范围内是可靠的，但是在频厚积很大时不再成立。

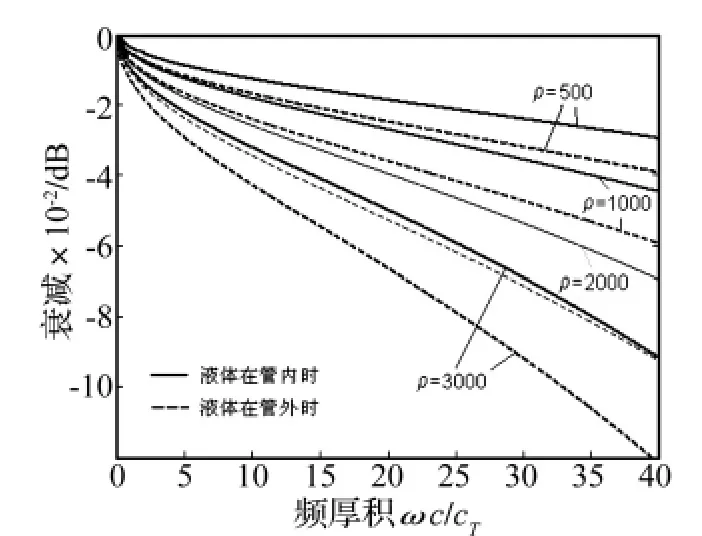
图13 液体在不同密度时T(0，1)模态的衰减曲线，密度单位为kg/m3，粘性系数为1 Pa·sFig.13 the normalized attenuation of the first torsional wave mode with different liquid density，the unit of density is kg/m3

5 结论

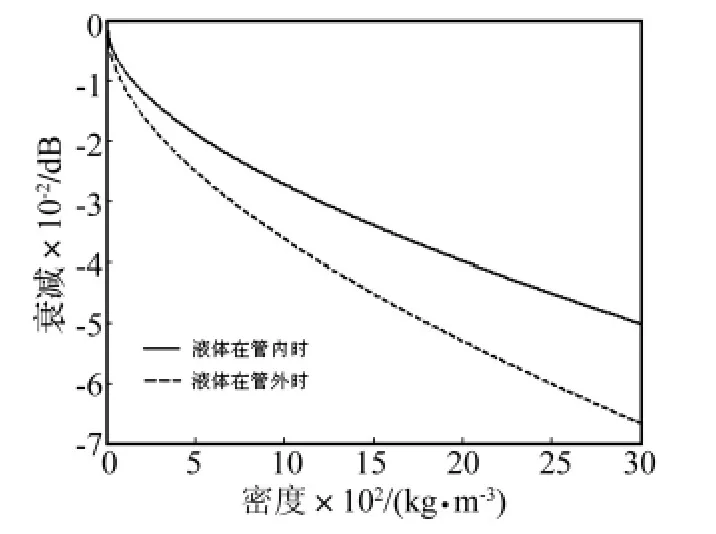
图14 当频率为1 MHz时液体密度与T(0，1)模态衰减的关系Fig.14 The relation between attenuation of the first torsional wave mode and liquid density，f=1 MHz

本文对带有粘性液体的管道中扭转导波的传播特性进行了分析。讨论了粘性液体对扭转波的频散曲线和衰减曲线的改变，研究了几种因素对于T(0，1)模态传播特性的影响。本文结果与液体在金属杆外侧时的实验结果符合较好，为T(0，1)模态在管道损伤检测中应用打下了一定基础。结果表明:

(1)管道扭转波在液体中的影响范围不大，波的运动仅限于靠近固壁的边界层中。

(2)粘性液体对于扭转波的频散特性改变不大，相速度的改变可以忽略，但对波的衰减有明显影响。除T(0，1)模态，更高阶模态的衰减比较相近。

(3)由于T(0，1)模态的频散很小，在扭转波中衰减最小，加上其位移分布的特点，在损伤检测中具有重要作用。

(4)液体的粘性和密度对T(0，1)模态的衰减都有较大影响，在频率较小时与衰减的平方成正比。

［1］Nagy P B，Nayfeh A H.Viscosity-induced attenuation of longitudinal guided waves in fluid-loaded rods［J］.Journal of Acoustical Society of America，1996，100(3):1501 －1508.

［2］ Barshinger J N，Rose J L.Guided wave propagation in an elastic hollow cylinder coated with a viscoelastic material［J］.IEEE Transactions on Ultrasonics， Ferroelectrics， and Frequency Control，2004，51(11):1547 －1556.

［3］L.Elvira-Segura，Acoustic wave dispersion in a cylindrical elastic tube filled with a viscous liquid［J］，Ultrasonics，2000，37:537－547.

［4］Aristegui C，Lowe M J S，Cawley P.Guided waves in fluidfilled pipes surrounded by different fluids［J］.Ultrasonics，2001，39:367 －375.

［5］ Ballandras S，Reinhardt A，Khelif A，et al.Theoretical analysis of damping effects of guided elastic waves at solid/fluid interfaces［J］.Journal of Applied Physics，2006，99:054907.

［6］刘增华，吴 斌，何存富，等.超声导波扭转模态在粘弹性包覆层管道中传播特性研究［J］.应用基础与工程科学学报，2005，13(3):291 －299.

［7］他得安，刘镇清，贺鹏飞，充粘液管材超声纵向导波的无损检测参数选择［J］.声学学报，2004，29(2):104－110.

［8］ Viens M，Tshukahara Y，Jen C，et al.Leaky torsional acoustic modes in infinite clad rods［J］.Journal of Acoustical Society of America，1994，95(2):701 －707.

［9］ Kwun H，Kima S Y，Choib M S.Torsional guided wave attenuation in coal-tar-enamel-coated，buried piping［J］.NDT＆E International，2004，37:663 －665.

［10］ Gazis D C.Three-dimensional investigation of the propagation of waves in hollow circular cylinders.I.analytical foundation［J］.Journal of Acoustical Society of America，1959，3(5):568－573.

［11］ Pavlakoivc B N，Leaky guided ultrasonic waves in NDT［D］.Imperial College，University of London，UK，1998.

［12］ Cebeci T，Cousteix J.Modeling and computation of boundarylayerflows［M］. Horizons Publishing Inc.， Long Beach，2005.

［13］ Vogt T，Lowe M J S，Cawley P.Ultrasonic waveguide techniques for the measurement of material properties［J］.Review of Quantitative Nondestructive Evaluation，2002，21:1742－1749.

［14］ Vogt T K，Lowe M J S，Cawley P.Measurement of the material properties of viscous liquids using ultrasonic guided waves［J］.IEEE Transaction on Ultrasonic，Ferroelectrics，and Frequency control，2004，51(6):737－747.