ND样本最近邻密度估计的一致强相合性
2012-09-07刘艳吴群英
刘艳,吴群英
(桂林理工大学理学院,广西桂林541004)
ND样本最近邻密度估计的一致强相合性
刘艳,吴群英
(桂林理工大学理学院,广西桂林541004)
设X1,X2,…,Xn是同分布的负相依(ND)样本,具有共同的密度函数f(x),利用相应的Bernstein不等式,将负相关(NA)样本最近邻密度估计的一致强相合性推广到ND样本,得到其最近邻密度估计的一致强相合性.
负相依序列;最近邻密度估计;一致强相合性;Bernstein不等式
概率密度估计和非参数非线性回归是非参数估计中两大问题.最近邻密度估计(NN-估计)是由Loftsgarden和Quesenberry[1]于1965年提出的.设X1,X2,…,Xn是来自未知密度f的样本,先选定一个与n有关的整数k=kn,1≤k<n,对固定的x∈R,记an(x)为最小的正数a,使得[x-a,x+a]中至少包含X1,X2,…,Xn中的k个.注意到,对每一个a>0可以期望在X1,X2,…,Xn中大约有2anf(x)个观察值落入区间[x-a,x+a]中.因而值f(x)的估计(记为^fn(x))自然地可以通过令k=2an^fn(x)得到.于是定义^fn(x)=k/2nan(x)为f(x)的估计.此后,许多著名学者都讨论过它的性质.对于独立样本,Wagner[2]证明了NN-估计的强相合性,陈希孺[3]证明了它的渐近正态性,而杨善朝[4]在一定条件下给出了NA序列下NN-估计的相合性.ND相依序列是比NA相依序列弱的一种数列,这些负相依随机变量的概念在可靠性理论、渗透理论和多元统计分析中均有广泛的应用.因此,将独立序列或NA序列的一些性质推广到ND序列是十分必要的.文献[5-7]分别讨论了ND序列完全收敛性、ND随机变量列的指数不等式等,但却很少触及NN-估计.而NN-估计在独立样本下已有很多优点,特别是计算简单,容易实施.因此,在ND样本下也应有一定的地位.本文在ND序列的基础上,讨论了ND序列的最近邻密度估计的一致强相合性.
1 定义及引理
假设总体X的分布密度函数为f(x),X1,X2,…,Xn是抽自该总体的ND样本;F(x)是密度函数f(x)相应的分布函数,是样本X1,X2,…,Xn的经验分布函数;c是与n无关的常数,在不同的地方可以表示不同的值.
定义1[5]称随机变量X1,X2,…,Xn,n≥2是ND的,若对∀x1,x2,…,xn∈R,都有

称随机变量列{Xn;n≥1}是ND列,如果对任意的n≥2,X1,X2,…,Xn是ND的.
从有限总体不放回抽样所得到的样本不是独立的,但是ND的.
引理1[5]设{Xn;n≥1}是ND的,∀m≥2,A1,A2,…,Am是集合{1,2,…,n}的两两不交非空子集.如果fi(i=1,2,…,m)是对每个变元都非降(或非升)的函数,则f1(Xj;j∈A1),f2(Xj;j∈A2),…,fm(Xj;j∈Am)仍是ND的.

2 主要结果
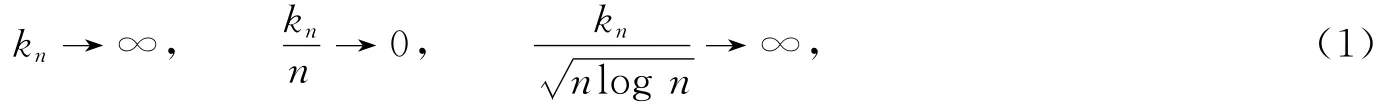
且f(x)在R上一致连续,则有

定理1 设{Xn;n≥1}是ND序列,kn满足
证明 ∀ε>0,P{|^fn(x)-f(x)|>ε}=P{^fn(x)>f(x)+ε}+P{^fn(x)<f(x)-ε},当f(x)<ε时,f(x)-ε的值为负值,由^fn(x)的非负性知,事件{^fn(x)<f(x)-ε}是不可能事件,故其概率为零.因此,对P{^fn(x)<f(x)-ε}的估计,只需考虑f(x)≥ε的情况.


3 应用举例
设在可靠性问题中r.v.X的分布函数记为F(x),密度函数为f(x),生存函数和失效率函数分别定义为F¯(x)=1-F(x)=P(X≥x)和r(x)=.又设X,X,…,X为从总体F(x)中抽取的同分12n布ND样本,则生存函数和失效率函数的自然估计为

定理2 设定理1的条件满足,则对任何满足F(c)<1的c,均
证明 记¯Fn(x)=1-F(x),¯Fn(x)=1-Fn(x),显然有

注意到0<F¯(c)≤F¯(x)≤1,∀x≤c,sup f(x)≤M<∞.由定理1和引理4知,sup|^fn(x)-f(x)|→
xx≤c0,a.s.,而且从而当n充分大时,对于x≤c,一致地有F¯(c)>F¯(x)-F¯(c)/2>F¯(c)/2>0.由这些事实和式(9)即得定理2的结论.证毕.
[1] LOFTSGARDEN D O,QUENSBERRY C D.A Nonparametric estimator of a multivariate density function[J].Ann Statist,1965,36(3):1049-1051.
[2] WAGNER T J.Strong consistency of a nonparametic estimate of a density function[J].IEEE Trans Systems Man Cybenet,1973(3):289-290.
[3] CHENG Xi-ru.Convergence rates for nearest neighbor density estimator[J].Sci China Ser A,1980(12):1419-1428.
[4] YANG Shan-chao.Consistency of nearest neighbor density function for pairwise NA sequence[J].Acta Math Application,2003,26(3):385-395.
[5] BOZORGNIA A,PATTERSON R F,TAYLOR R L.Limit theorems for ND r.v.′s[R].Athens:University of Georgia,1993.
[6] WU Qun-ying,JIANG Yuan-ying.The strong consistency of estimator in linear model for negatively dependent random samples[J].Communications in Statistics-Theory and Methods,2011,40(3):467-491.
[7] 杨善朝.NA样本最近邻密度估计的相合性[J].应用数报,2003,26(3):385-408.
Uniform Strong Consistency of Nearest Neighbor Estimator of Density Function for Negative Dependent Samples
LIU Yan,WU Qun-ying
(College of Science,Guilin University of Technology,Guilin 541004,China)
Suppose that X1,X2,…,Xnare negative dependent(ND)samples,with a common density function f(x).By the use of the corresponding Bernstein inequality,the uniform strong consistency of nearest neighbor estimator of density function for negatively associated(NA)samples is extended to ND samples,and the latter uniform strong consistency of nearest neighbor estimator of density function is obtained.
negative dependent sequence;nearest neighbor density estimator;Bernstein inequality
O 212.7
A
(责任编辑:黄晓楠 英文审校:黄心中)
1000-5013(2012)05-0590-05
2012-01-07
吴群英(1961-),女,教授,主要从事概率统计的研究.E-mail:wqy666@glite.edu.cn.
国家自然科学基金资助项目(11061012);广西自然科学基金资助项目(2011GXNSFA018147);广西研究生教育创新计划项目(2011105960202M32)
