经验模态分解阈值消噪方法及其在惯性导航系统数据处理中的应用

甘 雨，隋立芬，王 冰

信息工程大学测绘学院，河南郑州450052

经验模态分解阈值消噪方法及其在惯性导航系统数据处理中的应用

甘 雨，隋立芬，王 冰

信息工程大学测绘学院，河南郑州450052

针对惯性元件误差中有色噪声影响远大于白噪声的情况，建立元件误差的分形高斯噪声模型，利用功率谱密度方法估计模型参数。基于噪声模型推导经验模分解（EMD）的各固有模态函数（IMF）分量中噪声的方差，以此估计各分量相应的阈值，建立EMD阈值消噪方法。将该方法应用于INS中，并与小波阈值法进行比较。结果表明，小波阈值法难以控制元件中有色噪声的影响，EMD阈值法与噪声模型紧密结合，能够更有效地削弱元件中的随机误差，提高INS精度。

惯性元件；惯性导航系统；有色噪声；分形高斯噪声；经验模态分解；小波；阈值消噪

1 引 言

受到惯性元件误差等因素的影响，惯性导航系统（INS）的误差随时间积累［1］，虽然与卫星导航系统（GNSS）组合可以得到削弱，但是一部分元件误差的影响无法被GNSS探测到［2］。而且在GNSS不可用的情况下，单独INS的误差仍然得不到有效控制。惯性元件误差中确定性的部分可以进行相应补偿，而其随机部分难以建立精确模型，是制约INS精度的关键因素。

针对上述情况，有学者提出对惯性元件输出信号进行消噪处理来削弱惯性元件随机误差。其中基于经典选频滤波思想的数字低通滤波消噪法，无法解决元件输出中有用信号和噪声信号频带重叠的问题。小波分析具有时频多分辨特性［3］，惯性元件信号消噪主要应用小波阈值的方法［4－6］。文献［7］提出的小波阈值消噪方法，是专门针对信号中的高斯白噪声提出的一种消噪算法。当噪声为时间相关的有色噪声时，采用小波消噪效果不理想，对有色噪声的消噪到目前为止还未发现较好的方法［8］。惯性元件随机误差中存在大量有色噪声成分，如零偏不稳定性、速率随机游走和马尔可夫过程等，其影响远大于白噪声成分，这在中低精度元件中表现更为突出。现有的小波阈值消噪方法没有具体分析元件误差特性，直接按照白噪声模型估计各层小波系数的阈值，不能保证实际可靠性。

文献［9］提出的经验模分解（empirical mode decomposition，EMD）处理非线性非平稳信号的时频分析方法，基于信号本身自适应地从高频到低频逐次分解，获得一组固有模态函数（intrinsic mode function，IMF）分量［10］。该算法不但具有多分辨分析的优点，而且克服了小波分析需要选择基函数的困难，已有学者将其应用于信号消噪［11－13］。对于静态下元件信号，其中的有用成分频率极低，可以将高频IMF分量除去达到消噪的目的。但是对于动态下的信号，有用成分与误差存在大量混叠区域，需要对各IMF分量进行阈值处理。现有的EMD阈值消噪方法直接将小波阈值作用于IMF分量上，缺乏理论依据。

本文将阈值消噪的惯性元件随机模型由白噪声扩展为分形高斯噪声，以描述元件中依时间相关的有色噪声成分，利用功率谱密度方法估计模型参数。根据噪声模型推导EMD分解各IMF分量中噪声的方差特性，以此估计各分量相应的阈值，建立EMD阈值消噪的方法。用EMD阈值消噪方法对惯性测量单元（inertial measurement unit，IMU）动态条件下的输出信号进行处理并进行惯性导航解算，并与小波阈值消噪结果进行了比较。

2 惯性元件随机误差分形高斯噪声模型

2.1 分形高斯噪声

分形高斯噪声是高斯白噪声的扩展形式，本质上是个离散过程，其统计性质完全取决于二阶矩，而它的二阶矩依赖于唯一的参数H（称为Hurst参数，有0＜H＜1）。分形高斯噪声定义为［14］：零均值平稳高斯过程，且自相关函数如式（1）

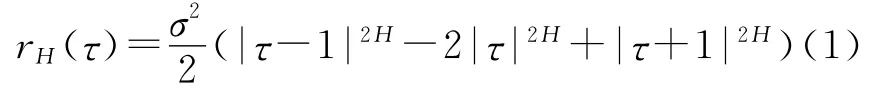
式中，τ为时延；σ2为方差，即rH（0）。

当τ→∞时，有［15］

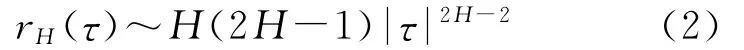
H＞0.5时，分形高斯噪声正相关且自相关函数衰减很慢；H＜0.5时，噪声负相关；特别的，H＝0.5时，有

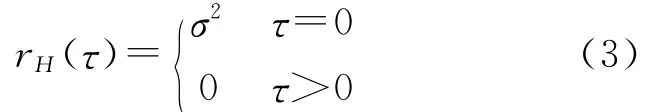
此时分形高斯噪声退化为高斯白噪声。

白噪声只能描述不相关的噪声过程，而分形高斯噪声可以根据Hurst参数H的变化来描述不同相关程度的噪声过程，扩展了噪声模型的适用范围。

2.2 元件随机误差的噪声模型

惯性元件随机误差中包含零偏不稳定性、速率随机游走、马尔可夫过程等噪声成分，导致惯性元件输出信号中的误差经常表现为有色噪声形式。因此，利用高斯分形噪声作为惯性元件随机误差的噪声模型，以反映有色噪声和白噪声的综合影响，其关键问题是估计惯性元件误差分形高斯噪声模型的参数H。

基于功率谱密度估计H是简单实用的方法［16］。分形高斯噪声的功率谱密度具有如下形式［14］

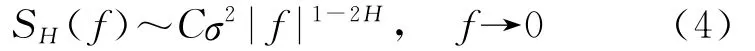
式中，f为频率；C代表常数。在奈奎斯特（Nyquist）频率范围内，式（4）均成立。取双对数，则

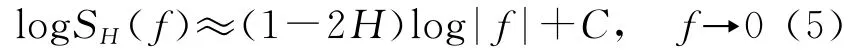
利用周期图法计算功率谱密度，将双对数功率谱密度按照（5）式进行最小二乘拟合，即可计算出H的估值，设拟合直线斜率为p，则

实用中，计算惯性数据的功率谱密度时常利用频率平均（frequency averaging）技术对谱进行平滑处理［17］，双对数谱密度进行拟合时通常选取80%～90%的低频部分［16］。

图1给出了某陀螺静基座下X轴输出信号的双对数功率谱密度，图2为谱密度平滑后的双对数形式以及所拟合的直线，H的估计结果为0.885，显然，该陀螺的随机误差不属于白噪声。

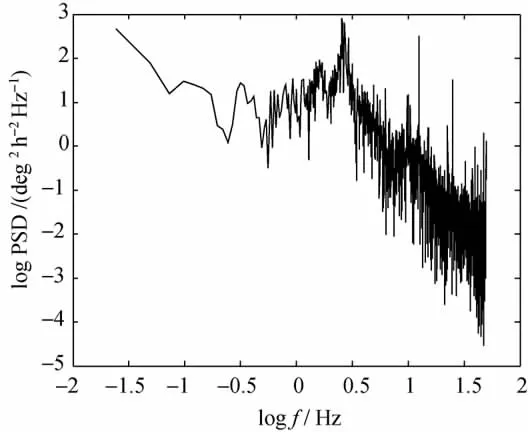
图1 X轴陀螺信号双对数谱密度Fig.1 Log－log PSD from X－gyro signal

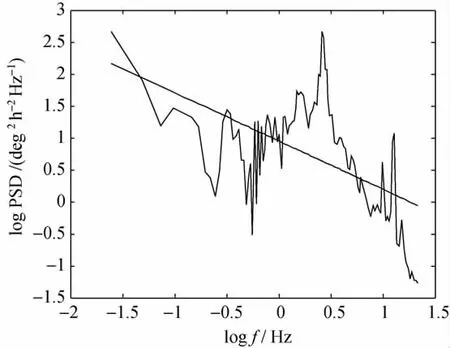
图2 X轴陀螺信号平滑双对数谱密度及拟合直线Fig.2 Smoothed log－log PSD fromX－gyro signal and the fitting line

3 EMD阈值消噪

3.1 EMD原理

EMD将复杂的信号分解成若干个按频率高低排列的IMF，每个IMF是一个零均值单分量信号。该方法与小波分析的区别在于它是后验的，不需要事先选定基函数，而是根据信号本身的特性自适应地产生合适的模态函数，这些模态函数能很好地反映信号在任何时间局部的频率特征。每个IMF分量满足：①零点数目与极值点数目相同或最多相差1；② 局部极大值点构成的包络线和局部极小值构成的包络线的均值为零。分解过程通过一个称为“筛选”的步骤来完成，具体操作请参见文献［9，18］。

经过“筛选”，原始信号x（t）可分解为n个IMF分量和1个余项的和

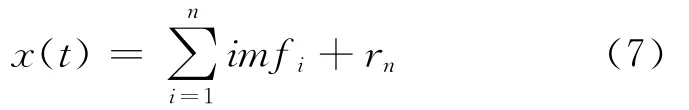
EMD分解出各IMF的瞬时频率之间的关系近似满足［14］：第1个IMF含最高瞬时频率成分，第i（i≥2）个IMF的瞬时频率几乎处处是第i＋1个IMF的瞬时频率的两倍。可见，IMF按照频率由高到低的顺序以此分解，一般来说，前几个IMF分量主要含有噪声成分，后续分量及余项主要包含有用信号成分，可借鉴小波阈值消噪的思想对前面m个分量进行阈值处理，达到削弱噪声的目的。

3.2 EMD阈值消噪方法

基于白噪声干扰假设的小波阈值方法难以有效削弱有色噪声，将小波阈值直接作用于各IMF分量的EMD阈值消噪方法会产生同样的问题。高斯分形噪声作为元件随机误差的噪声模型，可以描述随机误差中的有色噪声成分，符合实际应用的需求。动态条件下惯性元件输出信号包含有用信号和噪声，如果能够得到纯高斯分形噪声分解在各个IMF分量上的规律，便能估计出每一层的阈值。

文献［14］推导出了高斯分形噪声经EMD分解后产生的各IMF分量之间功率谱密度的关系

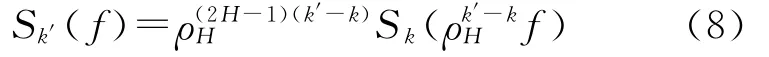
式中，k′＞k≥2；ρH为

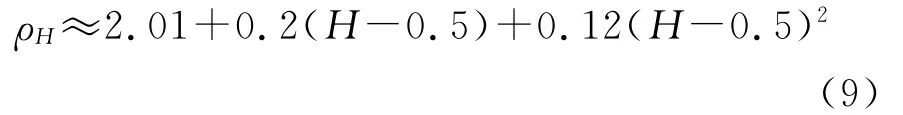
功率谱密度对频率的积分为方差，考虑到式（8），可推导出IMF分量方差之间的关系

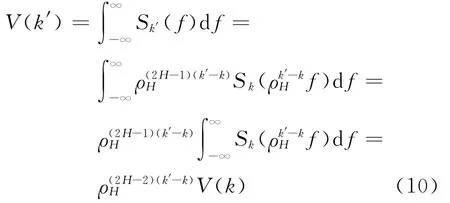
式（10）为纯高斯分形噪声EMD分解的IMF的方差规律（k′＞k≥2），利用方差关系，可估计出含噪声信号的阈值，对噪声进行处理。文献［19］在白噪声干扰的条件下借鉴小波阈值估计方法，提出EMD阈值取

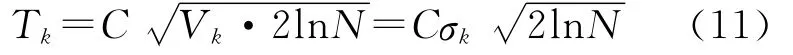
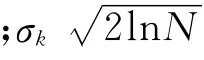
IMF分量的方差按下式估计

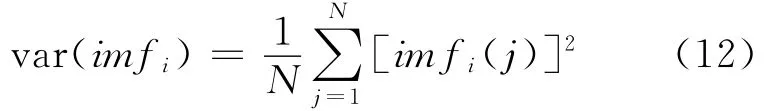
式（12）的方差是噪声和有用信号叠加的方差，而估计各IMF分量的阈值需要纯噪声的方差。前两个IMF分量的频率高，远远超出了有用信号频带范围，因此主要包含噪声成分，有用信号成分极少，对这两个分量进行抗差性标准差估计可获得纯分形高斯噪声的标准差

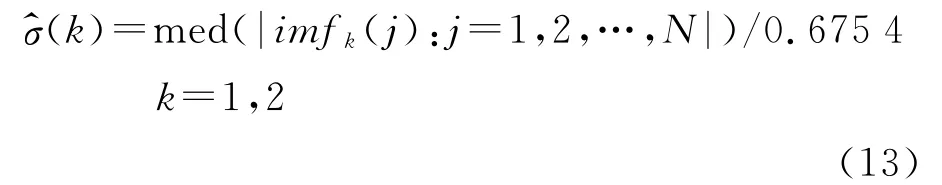
除前两个IMF外，其余分量可能含有较多有用信号成分，即使应用式（13）也未必能得到准确的纯噪声标准差。对于其余分量，利用式（10）进行计算，即

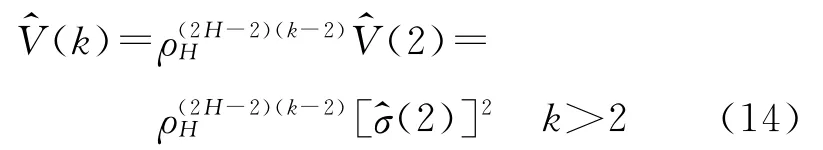
由式（13）及式（14）计算得到各个IMF所含噪声的标准差或方差，应用式（11）即计算出各IMF的阈值。

阈值消噪的策略主要包含硬阈值和软阈值两种［19］，软阈值的结果连续性和平滑性更好，但是可能会导致有偏的结果，在特定情况下还会产生多余的误差源［20］。软阈值对所有系数进行压缩，如果阈值估计产生误差，该误差会扩散到所有系数上；硬阈值只对低于阈值的部分进行处理，对高于阈值的部分保留，可以不受阈值估计误差的影响，因此EMD阈值消噪采用硬阈值策略，即

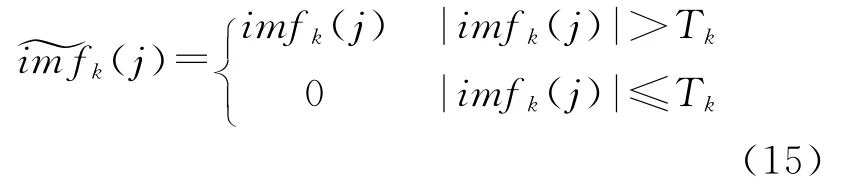
由于噪声成分主要集中于前面的IMF分量中，因此，无需将信号按式（7）进行完全的经验模分解，只需分解出前面m个分量的并进行阈值处理。前面提到，第i个IMF的频率几乎是第i＋1个IMF的频率的2倍，按照这个规律，对于惯性元件信号，第5、6个分解的IMF分量的频率已经很低，后续的分量中噪声成分极少。由于使用了硬阈值的消噪策略，分解个数m不是很敏感。因为随着m增加，IMF系数的大部分幅值高于阈值，阈值的作用越来越小。而软阈值将所有系数压缩，对分解个数m的选择十分敏感，错误的m会损失大量有用信号。

综上所述，基于高斯分形噪声模型的EMD阈值消噪的具体过程如下：

（1）利用式（5）、式（6）估计分形噪声参数H；

（2）对信号进行EMD分解，得到IMF分量；

（3）基于式（11）、式（13）、式（14）计算噪声标准差或方差，估计各IMF相应的阈值；

（4）按式（15）对分量中的系数进行硬阈值处理；

（5）按式（7）恢复消噪后的信号。

基于高斯分形噪声的EMD阈值消噪方法，将阈值估计算法与噪声模型相结合，克服了小波阈值消噪脱离误差统计特性的缺点。H为0.5时，对应于白噪声条件下的特殊情况，此时各IMF的方差不相同，因此阈值也不相同，而白噪声的各层小波分解系数方差一致，说明EMD与小波的分解特性有区别。

图3为动态条件下X轴陀螺某4096历元内输出信号EMD分解的前5个IMF分量，图4为IMF分量阈值消噪结果。显然，经验模分解阈值消噪方法在去除了以噪声为主的低幅值系数的同时，保留了可能含有有用信息的高幅值系数。

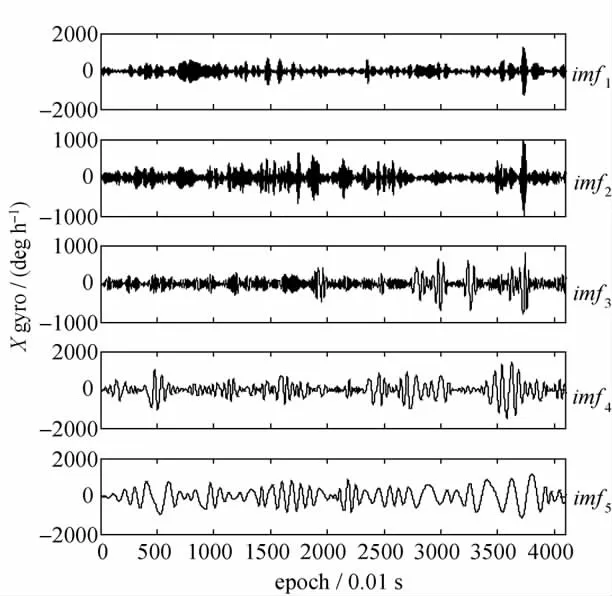
图3 信号EMD分解的IMF分量Fig.3 IMFs from EMD of signal

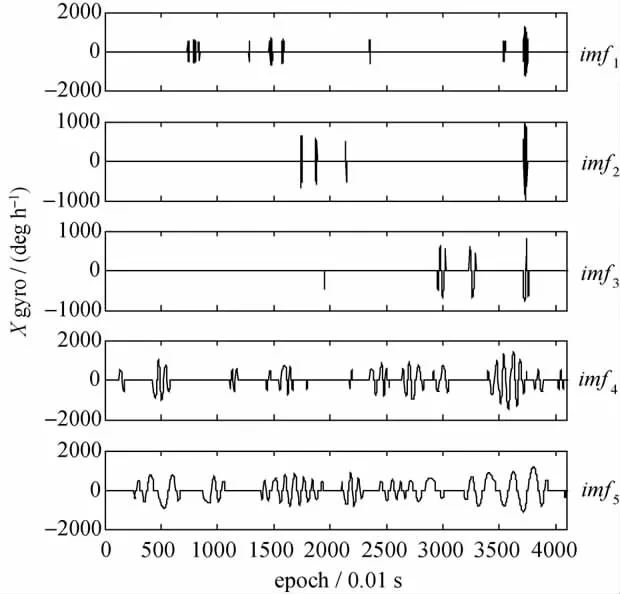
图4 EMD阈值消噪的IMF分量Fig.4 EMD threshold de－noised IMFs

4 计算与分析

使用一组动态战术级车载IMU（包含三轴陀螺和三轴加速度计）数据，IMU采样频率为100Hz。分别采取3种方案对IMU数据进行惯性导航解算，得到各历元的经纬度误差。

3种解算方案如下：

方案1 使用IMU输出的原始数据解算；

方案2 使用db8小波消噪后的IMU数据进行解算；

方案3 使用EMD阈值消噪后的IMU数据进行解算。

各轴陀螺输出信号如图5所示，IMU三轴分别对应于下、左、前方向。试验中，车辆主要在水平方向运动，因此X轴的旋转角运动比较剧烈，而Y、Z轴旋转角运动幅值较小，淹没于噪声中。任何阈值消噪方法均建立在有用信号幅值大于噪声幅值的基础上，因而对Y、Z轴不能进行阈值消噪。加速度计输出存在类似情况，Z轴加速度计幅值变化明显而X、Y轴有用信号被噪声淹没。因此，方案2、3只对X轴陀螺和Z轴加速度计数据进行阈值消噪处理，功率谱密度法估计的X陀螺和Z轴加速度计信号的Hurst参数值分别为0.885和0.447 4，EMD阈值处理的IMF个数为6，小波阈值取分解层数7，以4096宽度的历元窗口用阈值方法依次处理动态IMU数据。

3种方案的经纬度误差见图6和图7，点线、虚线、实线依次代表3种方案的结果。RMS和最大误差（max）的比较如表1所示。

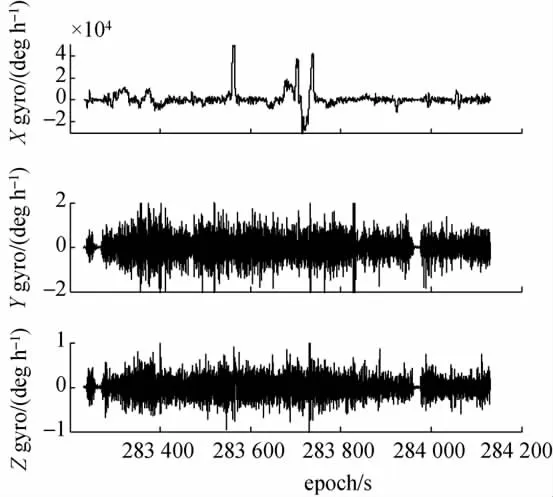
图5 陀螺输出信号Fig.5 Gyro signals

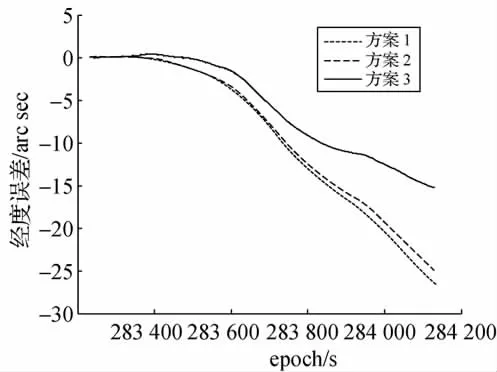
图6 经度误差Fig.6 Longitude errors

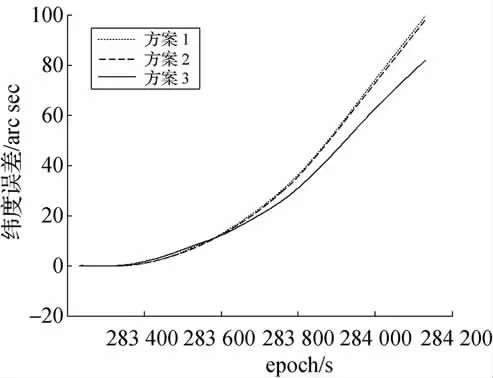
图7 纬度误差Fig.7 Latitude errors

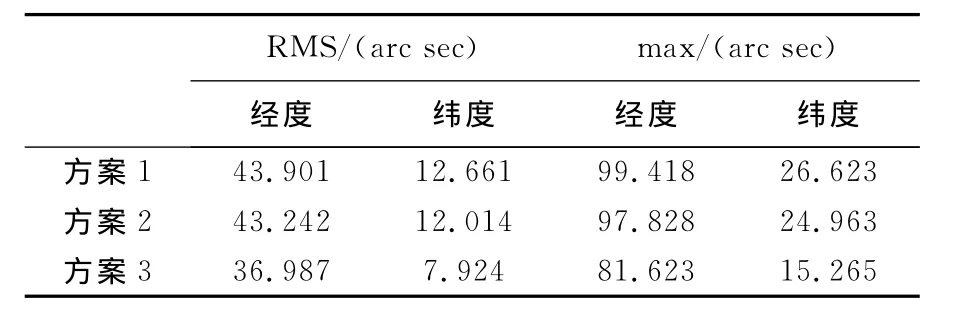
表1 3种方案RMS及max比较Tab.1 Comparison of RMS and max for three schemes

分析计算结果，可知

（1）小波阈值消噪方法能够削弱惯性元件中的白噪声干扰，提高导航精度。但消噪后的元件信号中还残余大量有色噪声成分，因此小波阈值消噪法的效果很有限。

（2）EMD阈值消噪方法建立在合理的分形噪声模型之上，对各IMF分量中的阈值估计准确，有效地削弱了元件随机误差中具有相关性的有色噪声成分，进一步提高了导航精度。

（3）受到Y、Z轴陀螺和X、Y轴加速度计中噪声的影响，对X轴陀螺和Z轴加速度计EMD阈值消噪后惯性导航误差仍然具有不断积累的趋势。

5 结 论

小波阈值消噪方法具有削弱白噪声的作用，但是应用于惯性元件随机误差消噪等问题时脱离了实际的噪声模型，难以控制元件中依时间相关有色噪声的影响。分形高斯噪声作为白噪声的扩展，能够描述噪声的相关性，适合作为惯性元件随机误差的噪声模型。建立在分形高斯噪声基础上的EMD阈值消噪方法，可以根据元件信号的误差特性进行阈值估计，有效削弱元件随机误差，提高INS及GNSS／INS组合导航的精度。

对于有用信号被噪声淹没情况下的消噪问题，目前还没有好的处理办法。如果有用信号的频率很低而噪声频率很高，如静止下的IMU数据，可以用EMD将IMF分量中的高频部分剔除达到消噪目的。但是如果动态IMU数据中某些轴向有用信号频带与噪声重叠而其幅值较小，则既不能通过剔除分量的方式消噪，也无法应用阈值的方式消噪。处理这类误差是下一步工作的重点。

［1］ GOODALL C L.Improving Usability of Low－cost INS／GPS Navigation Systems Using Intelligent Techniques［D］.Calgary：University of Calgary，Canada，2009.

［2］ ABDEL－HAMID W.Accuracy Enhancement of Integrated MEMS－IMU／GPS Systems for Land Vehicular Navigation Applications［D］.Calgary：University of Calgary，2005.

［3］ PENG Yunhui，LIU Yunfeng，YANG Xiaogan，et al.Application of Median Filter in Wavelet Domain in the Signal Processing of the Laser Gyro［J］.Infrared and Laser Engineering，2007，36（1），143－147.（彭云辉，刘云峰，杨小冈，等.小波域中值滤波在激光陀螺信号处理中的应用［J］.红外与激光工程，2007，36（1），143－147.）

［4］ WU Fumei，YANG Yuanxi.GPS／INS Integrated Navigation by Adaptive Filtering Based on Wavelet Threshold De－noising［J］.Acta Geodaetica et Cartographica Sinica，2007，36（2）：124－128.（吴富梅，杨元喜.基于小波阈值消噪自适应滤波的GPS／INS组合导航［J］.测绘学报，2007，36（2）：124－128.）

［5］ XIA Dunzhu，ZHOU Bailing，WANG Shourong.Application of Wavelet’s Real－time Filter in Silicon Micromachined Gyroscope［J］.Journal of Chinese Inertial Technology，2007，15（1）：92－95.（夏敦柱，周百令，王寿荣.实时小波滤波方法在硅微陀螺仪中的应用研究［J］.中国惯性技术学报，2007，15（1）：92－95.）

［6］ SU Li，ZHOU Xuemei.Application of Improved Wavelet Thresholding Method for De－noising Gyro Signal［J］.Journal of Chinese Inertial Technology，2009，17（2）：231－235.（苏丽，周雪梅.改进小波阈值法在MEMS陀螺信号去噪中的应用［J］.中国惯性技术学报，2009，17（2）：231－235.）

［7］ DONOHO D L，JOHNSTONE J M.Ideal Spatial Adaptation by Wavelet Shrinkage［J］.Biometrika，1994，81（3）：425－455.

［8］ JIANG Li，LI Changyun.A Study of Wavelet Threshold Filtering Based on Empirical Mode Decomposition［J］.Signal Processing，2005，21（6）：659－662.（江力，李长云.基于经验模分解的小波阈值滤波方法研究［J］.信号处理，2005，21（6）：659－662.）

［9］ HUANG N E，SHEN Z，LONG S R，et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis［J］.Proceedings of the Royal Society：A，1998，454（1971）：903－993.

［10］ WANG Jian，GAO Jingxiang，WANG Jinling.GPS Baseline Solution Based on Empirical Mode Decomposition［J］.Acta Geodaetica et Cartographica Sinica，2008，37（1）：10－14.（王坚，高井祥，王金岭.基于经验模态分解的GPS基线解算模型［J］.测绘学报，2008，37（1）：10－14.）

［11］ LIU Jin，MA Jie，TIAN Jinwen.Algorithm of Pulsar Signal De－noising Based on EMD［J］.Computer Engineering and Applications，2008，44（20）：212－214.（刘劲，马杰，田金文.基于EMD的脉冲星信号消噪算法［J］.计算机工程与应用，2008，44（20）：212－214.）

［12］ DAI Wujiao，DING Xiao 1i，ZHU Jianjun，et al.EMD Filter Method and Its Application in GPS Multipath［J］.Acta Geodaetica et Cartographica Sinica，2006，35（4）：321－327.（戴吾蛟，丁晓利，朱建军，等.基于经验模式分解的滤波消噪法及其在GPS多路径效应中的应用［J］.测绘学报，2006，35（4）：321－327.）

［13］ SONG Lixin，WANG Qi，WANG Yujing.ECG Signal Noise Reduction Using Hilbert－Huang Transform［J］.Chinese Journal of Sensors and Actuators，2006，19（6）：2578－2590.（宋立新，王祁，王玉静.基于Hilbert－Huang变换的ECG信号降噪方法［J］.传感技术学报，2006，19（6）：2578－2590.）

［14］ HUANG N E，SHEN S S P.Hilbert－Huang Transform and Its Applications［M］.Singapore：World Scientific，2005.

［15］ DIEKER A B，MANDJES M.On Spectral Simulation of Fractional Brownian Motion［J］.Probability in the Engineering and Informational Sciences，2003，17（3），417－434.

［16］ TAQQU M，TEVEROVSKY V，WILLINGER W，et al.Estimators for Long－range Dependence：An Empirical Study［J］.Fractals，1995，3（4），785－788.

［17］ Gyro and Accelerometer Panel of the IEEE Aerospace and Electronic System Society.IEEE STD 1293－1998／Cor 1－2008IEEE Standard Specification Format Guide and Test Procedure for Linear，Single－Axis，Nongyroscopic Accelerometers Corrigendum 1：Changes to Annex K and Annex L［S］.New York：Institute of Electrical and Electronics Engineers，1998.

［18］ GAN Yu，SUI Lifen.De－noising Method for Gyro Signal Based on EMD［J］.Acta Geodaetica et Cartographica Sinica，2011，40（6）：745－750.（甘雨，隋立芬.基于经验模分解的陀螺信号消噪［J］.测绘学报，2011，40（6）：745－750.）

［19］ KOPSINIS Y，MCLAUGHLIN S.Development of EMD－based Denoising Methods Inspired by Wavelet Thresholding［J］.IEEE Transactions on Signal Processing，2009，57（4），1351－1362.

［20］ CHIANG K.INS／GPS Integration Using Neutral Networks for Land Vehicular Navigation Applications［D］.Calgary：University of Calgary，2004.

E－mail：ganyu099＠163.com

EMD Threshold De－noising and Its Applications in INS Data Processing

GAN Yu，SUI Lifen，WANG Bing
Institute of Surveying and Mapping，Information Engineering University，Zhengzhou 450052，China

Since colored noise is predominant in sensor errors，fractional Gaussian noise model is established and the model parameter estimation method by power spectral density is given.Noise variance in intrinsic mode functions（IMFs）from empirical mode decomposition（EMD）is derived.Noise thresholds of IMFs are estimated through variance and EMD threshold de－noising method is established.The method is applied in INS and compared with wavelet de－noising method.It is shown that wavelet threshold de－noising is poor at suppressing colored noise while EMD threshold de－noising is effective on reducing sensor errors for its connection with proper noise model.INS accuracy is improved through EMD threshold de－noising.

inertial sensors；INS；colored noise；fractional Gaussian noise；EMD；wavelet；threshold de－noising

GAN Yu（1988－），male，postgraduate，majors in dynamic geodetic data processing.

GAN Yu，SUI Lifen，WANG Bing.EMD Threshold De－noising and Its Applications in INS Data Processing［J］.Acta Geodaetica et Cartographica Sinica，2012，41（4）：504－509.（甘雨，隋立芬，王冰.经验模态分解阈值消噪方法及其在惯性导航系统数据处理中的应用［J］.测绘学报，2012，41（4）：504－509.）

P228

A

1001－1595（2012）04－0504－06

国家自然科学基金（40974010；41174006）

丛树平）

2011－08－26

2012－01－02

甘雨（1988－），男，硕士生，研究方向为动态大地测量数据处理。