纳伪概率可控的四舍五入法及其在RTK模糊度固定中的应用

李博峰，沈云中，张兴福

1.同济大学 现代工程测量国家测绘地理信息局重点实验室，上海200092；2.同济大学 测量与地理信息学院，上海200092；3.广东工业大学测绘工程系，广东广州510006

纳伪概率可控的四舍五入法及其在RTK模糊度固定中的应用

李博峰1，沈云中2，张兴福3

1.同济大学 现代工程测量国家测绘地理信息局重点实验室，上海200092；2.同济大学 测量与地理信息学院，上海200092；3.广东工业大学测绘工程系，广东广州510006

RTK模糊度固定通常采用序贯四舍五入方法，该方法只固定能可靠固定的部分模糊度，因此控制四舍五入的纳伪概率是实现RTK可靠性的关键。从含多个备选假设的假设检验理论出发，研究纳伪概率可控的四舍五入方法，根据风险水平和实数解的质量自适应地确定四舍五入取整区域，从而有效地控制整数固定的纳伪概率。并结合GNSS应用中两种特殊情况，发展两种简单实用的应用策略。采用基线长94.6 km的CORS站GPS双频数据进行网络RTK模糊度固定试验，分析本文纳伪概率可控的四舍五入方法的效果。结果表明，纳伪概率可控的四舍五入方法的固定率与传统四舍五入方法的固定率相当，且较传统方法更能有效地控制纳伪概率，提高整数解的可靠性。

实时动态定位；四舍五入；纳伪概率；多个备选假设；假设检验

1 引 言

整数模糊度固定是实现高精度GNSS应用的前提，整数固定方法包括两个方面：整数估计准则和整数搜索算法［1］。常用的整数估计准则有四舍五入、Bootstrapping和整数最小二乘（ILS）［2］，以及快速模糊度固定的病态正则化准则［1，3－7］。整数搜索算法的实质是通过构造整数不等式约束条件（如整数统计量）快速剔除错误的备选模糊度组合［8－14］。

整数模糊度的可靠性是实现高精度GNSS应用的前提，一旦固定错误，往往会导致固定解反比实数解差。因此，必须严格控制整数解的质量。与实数估计理论不同，整数的离散性使得无法用协方差阵来刻画它的质量［15］，通常采用成功概率，即实数解落入由整数估计准则所确定的整数映射实数子空间的概率［16－21］。值得指出的是，目前为止，所有的整数可靠性理论都是以实数估值无偏为前提，该条件在GNSS应用中很难满足，因为大气延迟、多路径效应等系统误差影响极其复杂，无法用精确的函数模型表达。事实上，由于这些系统性误差引起的模糊度错误固定也正是模糊度质量控制的关键与难点所在。

RTK初始化后只需求解后续观测引入的新模糊度，未知模糊度向量往往只包含几个（甚至1个）模糊度。这些模糊度由于观测几何强度不同而精度差异较大，不可能同时可靠地固定。而目前广泛使用的LAMBDA方法只是加快搜索速度，并不能提高固定解的可靠性［22］。因此，RTK模糊度固定通常采用Bootstrapping方法只固定能可靠固定的部分模糊度。Bootstrapping的本质是序贯四舍五入［23］，其可靠性依赖于四舍五入的可靠性，因此控制四舍五入的纳伪概率是实现RTK可靠性的关键。目前，主要有两种控制四舍五入可靠性的策略。一种策略是给定小数和方差阈值（fixed－fraction－variance，FFV），若实数估值同时满足小数和方差阈值，则固定；另一种策略则是给定成功概率阈值，若实数解对应的成功概率大于该阈值，则固定。这两种方法都存在缺陷：第1种方法的阈值很难确定，阈值过大会导致纳伪概率增大，过小会降低固定效率，且阈值不随实数解的质量而变化；第2种方法只考虑实数解的精度，忽略了实数解本身的质量。

本文研究纳伪概率可控的四舍五入方法，从含多个备选假设的假设检验理论出发，根据风险水平和实数解的质量，自适应地确定实数解的取整区间，从而严格地控制整数解的纳伪概率，提高固定解的可靠性。此外，结合GNSS应用的两种特殊情况，发展了两种简单实用的应用策略。

2 四舍五入法及其两类错误概率

2.1 四舍五入法与含多个备选假设的假设检验

假设GNSS观测值服从正态分布，则最小二乘实数模糊度估值也服从正态分布～N（a，），其中，a∈Z和分别是的期望和方差。根据整数容许估计的整数平移不变性，平移整数a后的实数模糊度服从正态分布～N（0），对应的概率密度函数为

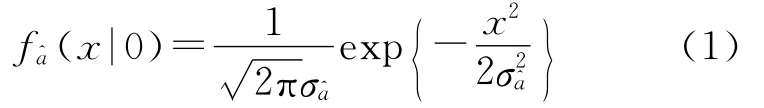
对于含两个备选假设（即原假设与备选假设）的假设检验问题，拒绝原假设等价于接受备选假设，对应弃真和纳伪两类错误。而对于含多个备选假设的假设检验问题，拒绝某一备选假设并不意味总是接受另一特定备选假设，而有可能接受另外任一备选假设，因此不存在笼统的弃真和纳伪错误，只存在相对于某个备选假设的弃真和纳伪错误。为表述方便，将四舍五入固定解集分为正确固定和错误固定两类，记

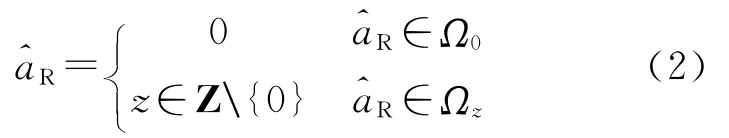
式中，Ωz表示固定解z对应的实数空间。采用含两个备选假设的假设检验问题的表述方式，令原假设

将其余所有备选假设笼统归为备选假设

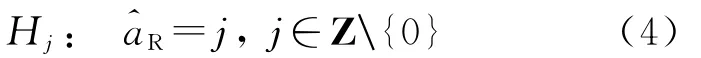
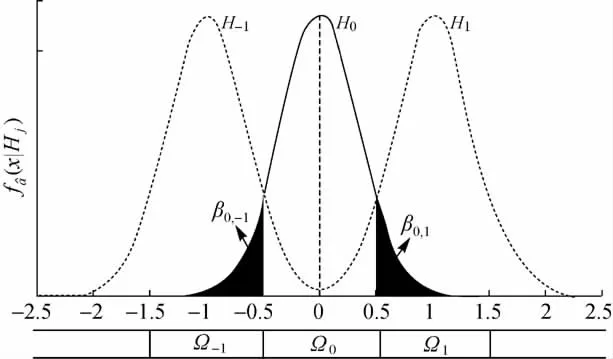
图1 四舍五入对应的多个备选假设接受域Fig.1 The acceptance regions of multiple hypotheses for integer rounding

图1给出了四舍五入对应的多个备选假设（H0、H1和H－1）示意图。令βj，i表示当Hj为真但接受备选假设Hi的错误概率，则

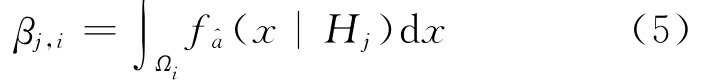
根据含多个备选假设的假设检验理论，当Hk为真但接受其他备选假设Hi（z∈Z＼｛k｝）的概率（即Hk的弃真概率）为

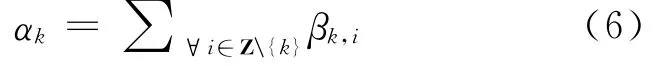
相应的，错误地接受Hk的概率（即Hk的纳伪概率）为

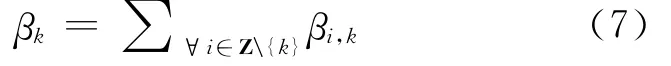
对应的检验功率（即正确接受Hk的概率，也称为成功概率）为

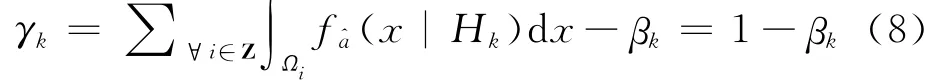
2.2 四舍五入法的两类错误概率

由似然比检验准则得备选假设Hi的接受域为［24］

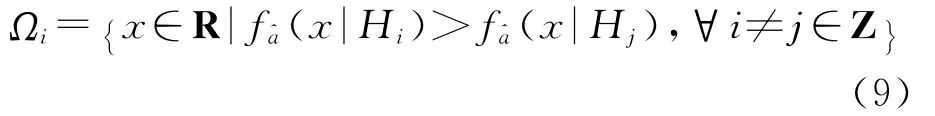
易证

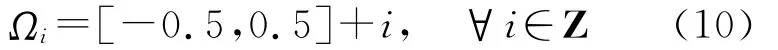
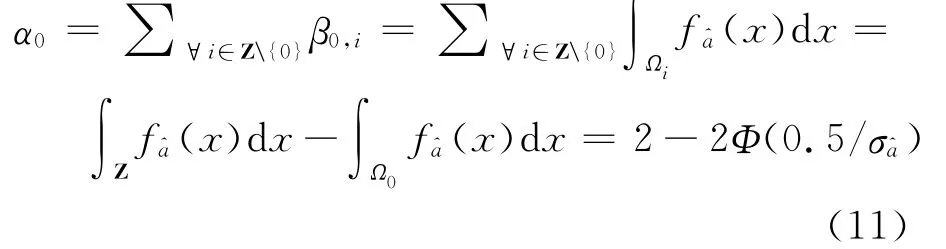
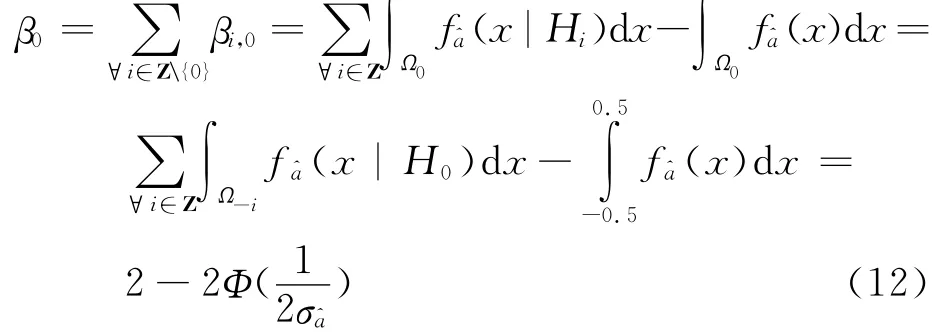
因此α0≡β0。按式（8）计算正确接受H0的概率（成功概率）为

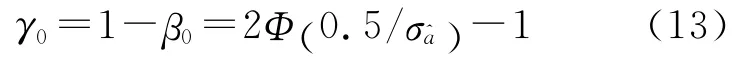
实际应用中，即使检验结果是拒绝原假设H0，也并不接受其他备选假设，而保留实数解。因此，弃真错误只影响整数固定的效率；一旦检验接受H0，则意味着接受固定解，因此，纳伪错误相当于采用了错误的固定解，必须严格控制。由式（12）得出，纳伪概率β0与概率密度函数（x）及接受域Ωi有关。

由于传统四舍五入法的备选假设接受域Ωi＝［－0.5，0.5］＋i固定，故纳伪概率只与实数解的精度有关。换言之，一旦给定了实数估值，四舍五入的纳伪概率就唯一确定。受传统假设检验可通过改变拒绝域来调节弃真、纳伪概率的思想启发，本文尝试改变四舍五入接受域Ωi来严格控制纳伪概率，提高整数固定的可靠性。

3 纳伪概率可控的四舍五入法

3.1 改变四舍五入区间控制纳伪概率

设四舍五入取整区间［－0.5，0.5］缩小为［－r，r］，0≤r≤0.5，则原假设H0的接受域Ω0变为

备选假设Hi的接受域变为

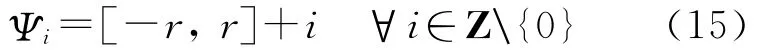
显然，Ψi⊆Ωi且

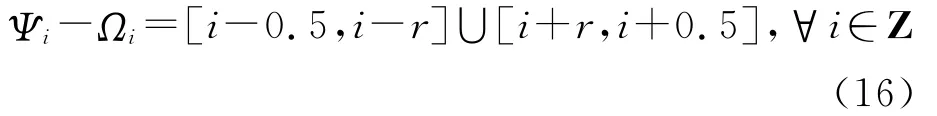
整数解集对应的实数空间为

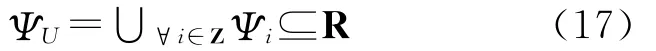
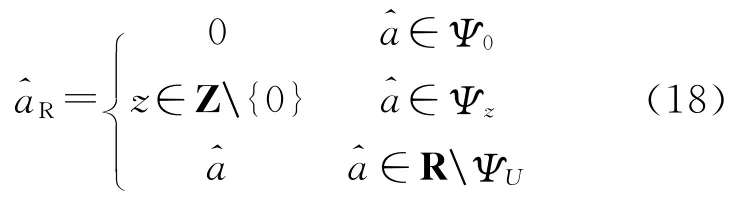
图2给出了缩小取整区间后的多个备选假设H0，H1和H－1对应的接受域示意图。

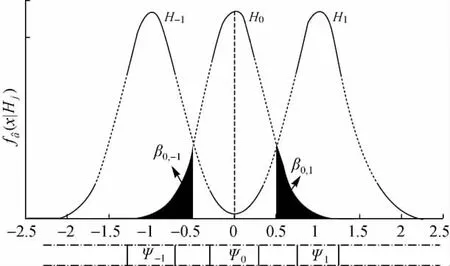
图2 缩小四舍五入区间的多个备选假设对应的接受域Fig.2 The acceptance regions of multiple hypotheses for integer rounding with shrunken region

缩小取整区间后的原假设H0的纳伪概率为

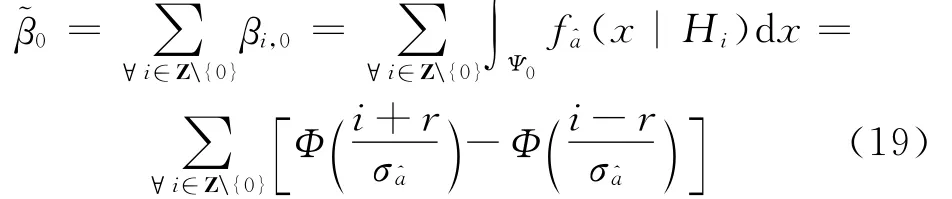
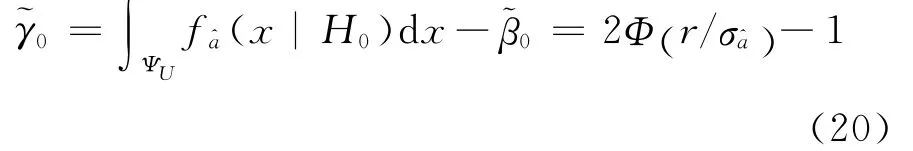
比较缩小取整区间前后的纳伪概率之差

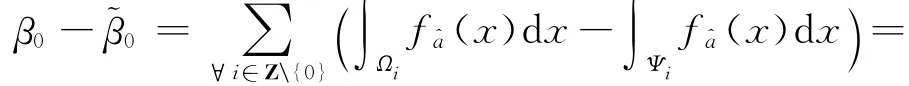
正确接受H0的概率（成功概率）为

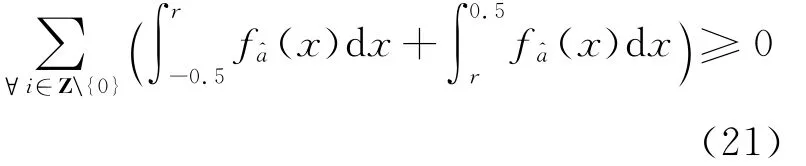
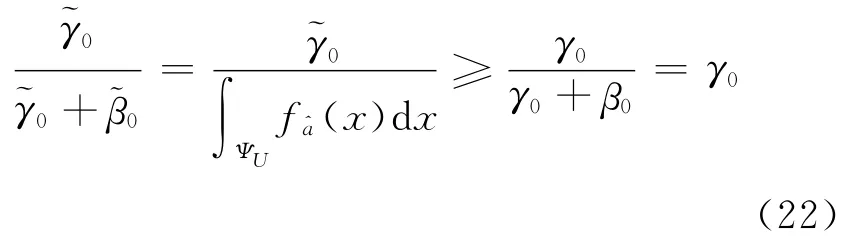
缩小取整区间四舍五入法的本质是通过缩小取整区间，保留那些容易错误固定的实数解不固定，从而严格控制纳伪概率，提高固定解的可靠性。

3.2 四舍五入区间的确定

确定合理的取整区间半径r是提高模糊度固定可靠性的关键。r过小，放弃了固定原本能正确固定的模糊度，降低了固定效率；r过大，则不能有效地控制纳伪概率。因此，必须在严格控制纳伪概率的同时自适应地确定r。首先注意到纳伪概率的计算涉及无穷个整数概率的累加，实际计算只能取有限个整数，即忽略那些极小概率对应的整数。根据式（19），整数i的绝对值越大，它对的贡献越小，即∀i＞j＞0，则

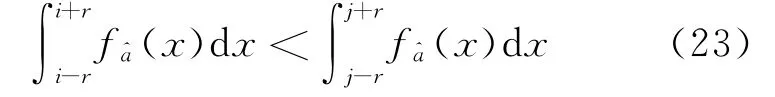
给定极小量μ，若整数i0满足

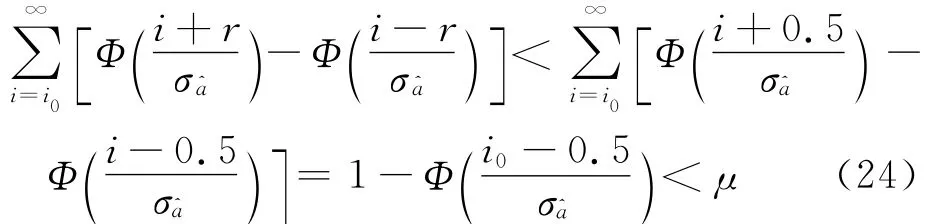
只需计算小于i0的整数对的贡献，引入的概率误差小于μ。图3给出了在不同的μ下，实数解精度与i0的关系，表明实数解精度越高，需要计算的整数个数越少；即使当实数解精度达到0.5周时，亦只需计算4个整数对应的概率。

确定i0后，纳伪概率式（19）简化为

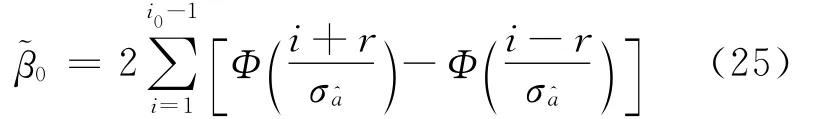
式中，σ＾a由实数估值确定，用户可设定能承担的风险水平βmax，根据＜βmax确定r。如图4所示，实线下方区域为当βmax＝0.01%时的四舍五入取整区域（下文称βmax区域）。显然，r随着σ＾a的增大而减小，即实数解精度越差，要求实数解越接近整数。

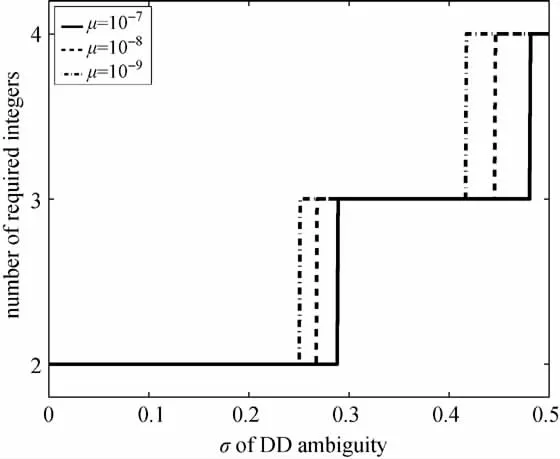
图3 整数个数与模糊度精度及概率误差阈值μ关系Fig.3 The number of integers versus the ambiguity precisions under the different thresholdsμ

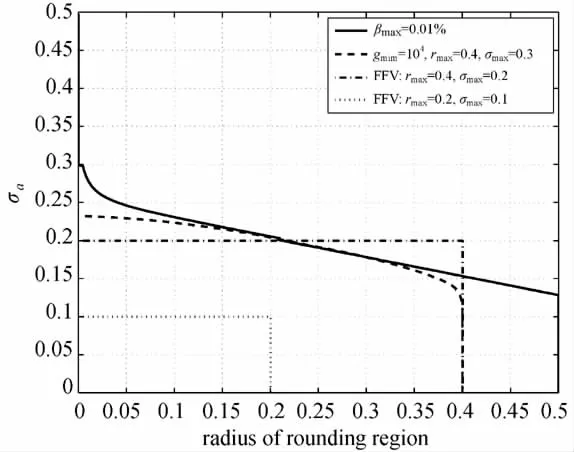
图4 实数解精度与四舍五入区间半径的关系Fig.4 Relationship between precision of real－valued estimate and radius of rounding region

3.3 两种特殊情况的处理

理论上，只要实数估值落入βmax区域就能以小于βmax的纳伪概率固定。实际应用存在两种特殊情况：

（1）实数解精度很高，但小数部分接近0.5，对应βmax区域的右下部分。该情况的发生是由于残留的系统误差导致实数解存在偏差。

（2）实数解精度较差，但小数部分接近0，对应βmax区域的左上部分。该情况的发生是由于观测模型的几何强度不够，小数接近0纯属偶然现象。

显然，这两种情况都需排除，否则纳伪概率依然不能有效控制。本文提出的两种方法在控制纳伪概率的同时，排除两种特殊情况。

类似于传统的FFV方法，第1种方法给定实数解的小数和精度限差排除βmax区域内的这两种特殊情况，该方法的取整区域为

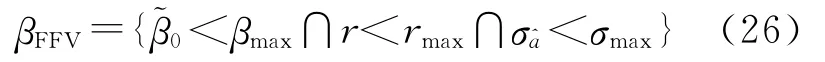
式中，rmax≤0.5和σmax是用户给定的实数解的小数和精度限差。

另一种方法是通过构造T型函数来排除两种特殊情况［23］，本文给出T型函数广义形式

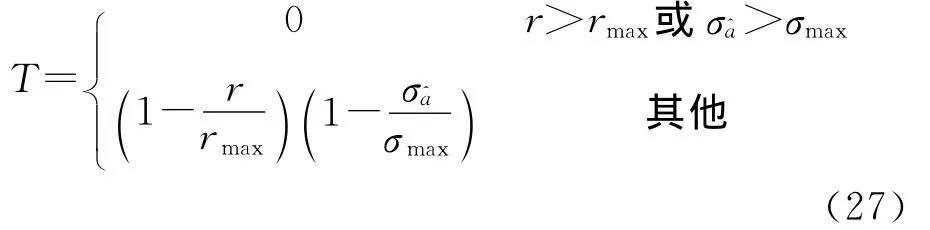
考虑到模糊度固定除了控制纳伪概率外，还应尽可能地提高模糊度固定效率，构造目标函数

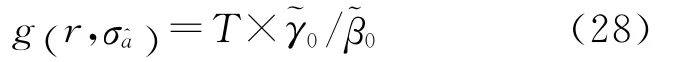
设定rmax、σmax和限差gmin，若实数解满足g＞gmin，则固定。为了有效地控制纳伪概率，限差gmin与βmax的取整区域应接近，取gmin＝104，rmax＝0.4，σmax＝0.3，图4虚线的下方区域为gmin的取整区域，显然该区域与式（26）确定的取整区域非常接近。

上述公式推导是先根据实数解的精度σ＾a和风险水平βmax确定取整区间半径r，然后比较r与实数解的小数。实际应用可倒过来执行，先直接以实数解的小数作为取整区间半径r，然后按照式（25）计算纳伪概率。若采用第1种方法，判断实数解是否满足式（26），满足则固定，否则保留实数解；若采用第2种方法，还需按式（20）和式（27）计算和T，并按式（28）计算g，若g＞gmin，则固定，否则保留实数解。

4 算例分析

采用基线长94.6km的两个CORS站3h GPS双频数据进行网络RTK模糊度固定试验，采样间隔1s，截止高度角10°，采用所有数据正确固定所有模糊度作为后续分析参考值。附宽巷模糊度约束的单历元电离层加权双差观测方程为

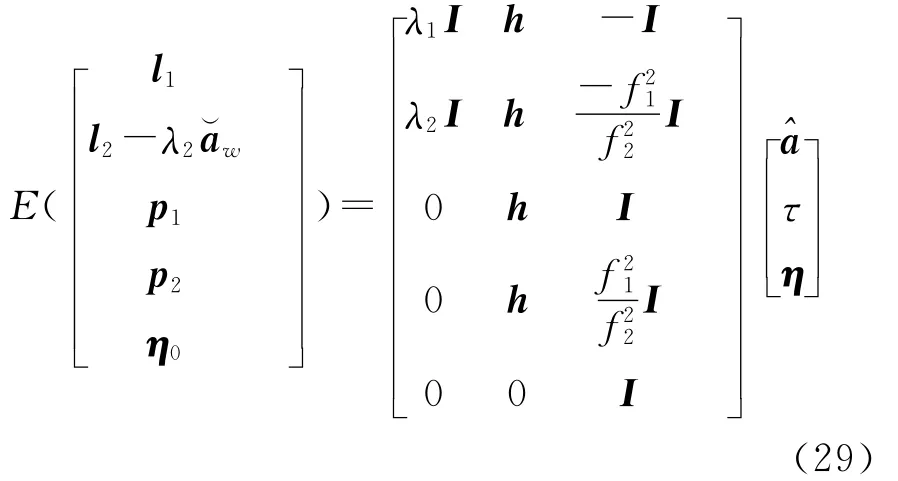
式中，l1、l2、p1和p2分别为经卫地距改正后的L1和L2双差相位和伪距观测值；为整数宽巷模糊度为L1双差模糊度；τ为相对天顶对流层延迟且短时间内不变；h是它的设计矩阵；η是双差电离层延迟参数；η0为双差电离层延迟的先验值，通常取0；I是单位阵，观测误差的协方差阵为

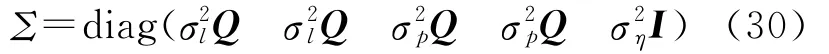
式中，σl＝5mm和σp＝0.5m分别为双差相位和伪距观测值的精度；Q为单历元双差观测值的协因数阵；ση＝15cm为双差电离层延迟的先验精度。采用多历元数据最小二乘平差计算实数模糊度向量＾a及它的协方差矩阵，然后采用Bootstrapping方法按高度角从高到低依次固定模糊度。在四舍五入取整中，比较以下5种方案：

方案1 传统FFV方法，取阈值rmax＝0.2，σmax＝0.1，取整区域对应图4点线的左下方区域。

方案2 传统FFV方法，取阈值rmax＝0.4，σmax＝0.2，取整区域对应图4点划线左下方区域。

方案3 纳伪概率可控的方法但未排除两种特殊情况，取阈值βmax＝0.01%，取整区域对应图4的实线下方区域（即βmax区域）。

方案4 本文提出的第1种方法，纳伪概率可控且结合FFV排除两种特殊情况，取阈值rmax＝0.4，σmax＝0.3，取整区域对应式（26）定义的βFFV区域。

方案5 本文提出的第2种方法，纳伪概率可控且排除两种特殊情况，取阈值rmax＝0.4，σmax＝0.3、gmin＝104，取整区域对应图4虚线左下方区域。

首先采用10个历元的观测数据计算得到1500个实数模糊度向量，共计约6200个模糊度。对于每个模糊度向量，采用Bootstrapping方法按高度角从高到低依次固定模糊度，即先固定高度角最高的模糊度，然后假设该模糊度正确固定，采用其参考值改正其余模糊度，然后再固定高度角次高的模糊度，以次类推，固定所有的模糊度。

图5直观地展示了纳伪概率可控（βmax＝0.01%）的取整区域与所有6200个实数模糊度的分布，落入实线区域内的模糊度可以固定，显然，当实数模糊度接近整数时，可适当放宽对其精度的要求。为了验证纳伪概率可控的四舍五入方法在实际应用中的确能够严格地控制纳伪概率，图6给出了方案2和方案3的固定模糊度对应的纳伪概率，方案3的所有固定模糊度的纳伪概率都小于0.01%，而方案2有些固定模糊度的纳伪概率远大于0.01%，说明方案2对应的传统FFV方法不能有效地控制模糊度固定的纳伪水平。

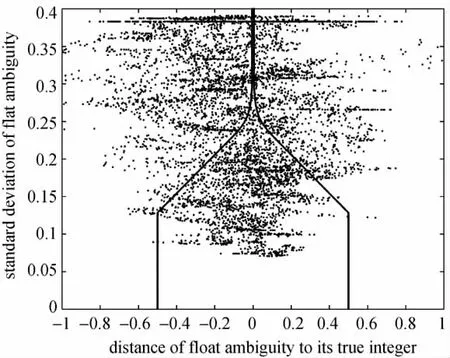
图5 实数模糊度及纳伪概率可控（βmax＝0.01%）的取整区域Fig.5 The float ambiguities and the error probability controllable acceptance region of integer rounding

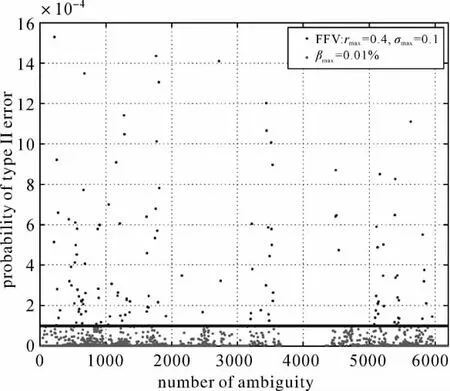
图6 方案2和方案3固定的模糊度对应的纳伪概率Fig.6 The error probabilities of the fixed ambiguities with respect to the schemes 2and 3

为了分析不同方案在不同实数解质量下的模糊度固定效果，分别采用3～10个历元的数据计算实数模糊度，然后采用Bootstrapping方法固定模糊度，再采用不同的四舍五入方案固定模糊度。图7给出了所有方案采用不同历元数据的模糊度固定概率，随着历元数的增加，模型强度增强，模糊度实数解质量提高，固定概率增大。图8给出了所有方案采用不同历元数据固定模糊度的纳伪概率，随着历元数的增加，纳伪概率也有所增大。方案1的取整区域控制过于严格，导致固定概率过低，10个历元的固定概率依然小于5%；当然过于严格的取整区域能有效地减小纳伪概率，如图8所示，它的纳伪概率始终接近0。方案2能有效地提高固定概率，但纳伪概率未能得到有效控制，10个历元的纳伪概率达到1.5%。方案3采用纳伪概率可控的四舍五入策略能根据实数模糊度质量调节取整区域，与方案2相比，固定概率提高了4%，但它们的纳伪概率相当；尤其当历元数小于8时，方案3的固定概率大于方案2且纳伪概率小于方案2，故方案3比方案2更加合理。

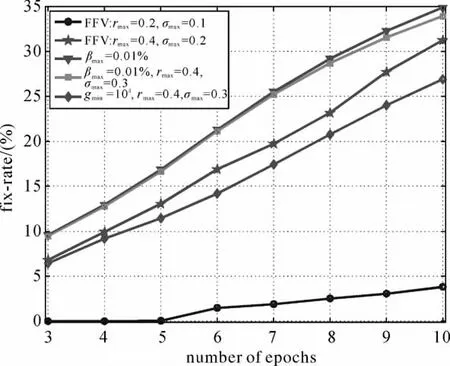
图7 各种方案不同历元数据的固定概率Fig.7 The fix－rates versus the number of epochs for the different rounding schemes

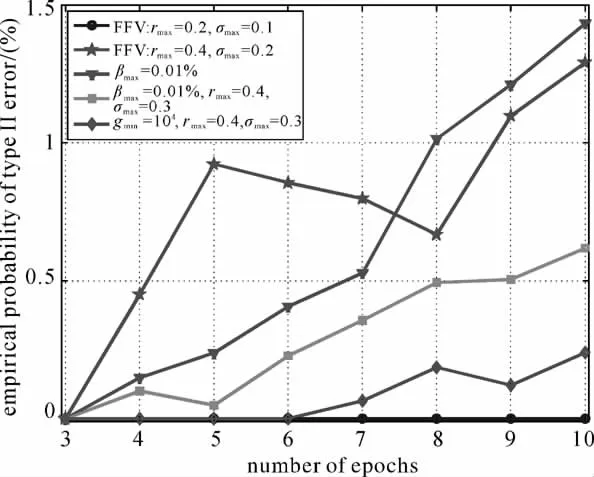
图8 各种方案不同历元数据的错误固定概率Fig.8 The error probabilities of the fixed ambiguities for the different rounding schemes

理论上，方案3的纳伪概率统计意义上应该小于风险水平βmax＝0.01%，而实际结果却远大于βmax（如图8所示），原因是方案3以实数模糊度估值无偏为理论基础，而未考虑本文提到的实际应用中的两种特殊情况，因此，采用本文提出的两种四舍五入方法（即方案4和方案5）有望较方案3减小纳伪概率。比较方案4与方案3，它们的固定概率相当，但方案4的纳伪概率比方案3减小约一倍。比较方案5与方案3，由于方案5的取整区域更加严格（参考图4），固定概率较方案3有所减小（相对减小22.8%），但方案5的确能更加严格地控制纳伪概率，纳伪概率从1.5%减小到0.2%（相对减小86.7%）。因此，在实际应用中，若可承受适当放宽的纳伪概率，可采用本文提出的第1种四舍五入方法得到高的固定概率（即试验方案4）；若倾向于严格控制纳伪概率，可采用本文提出的第2种四舍五入方法（即试验方案5）。

5 结 论

RTK模糊度固定通常采用序贯四舍五入法固定只能可靠固定的部分模糊度，其可靠性依赖于四舍五入法的可靠性。而目前采用的FFV和给定成功概率阈值的策略都存在理论或者应用上的缺陷。本文提出了根据风险水平和实数解质量自适应确定四舍五入取整区间从而控制纳伪概率的方法，并结合GNSS应用中的两种特殊情况，提出了两种简单实用的四舍五入取整方案。研究表明：① 缩小四舍五入取整区间的本质是放弃固定容易错误固定的实数解，从而严格控制了纳伪概率，提高了固定解的可靠性；②传统FFV策略很难确定合理的阈值，阈值过小，虽能严格控制纳伪概率但其固定效率过低，阈值过大，虽能提高固定效率，但纳伪概率不能有效控制；③ 采用纳伪概率可控的四舍五入法，若不考虑实际应用中的两种特殊情况，纳伪概率依然不能有效控制；④采用本文提出的第1种方法，即控制纳伪概率同时给定实数解的小数和精度阈值排除两种特殊情况，能有效地控制纳伪概率且保持高的固定概率；⑤ 采用本文提出的第2种方法，即采用目标函数g，能以固定概率的略微减小换来纳伪概率的严格控制。因此，在实际应用中，若可容忍略微放宽的纳伪概率（如常规RTK），可采用本文提出的第1种方法获得高的固定概率；若倾向于严格控制纳伪概率（如网络RTK），可采用本文提出的第2种方法。

［1］ LI Bofeng，FENG Yanming，SHEN Yunzhong.Extended GNSS Ambiguity Resolution Models with Regularization Criterion and Constraints［J］.Journal of Global Positioning Systems，2009，8（2）：149－154.

［2］ TEUNISSEN P.An Optimality Property of the Integer Least－squares Estimator［J］.Journal of Geodesy，1999，73：587－593.

［3］ OU Jikun，WANG Zhenjie.An Improved Regularization Method to Resolve Integer Ambiguity in Rapid Positioning Using Single Frequency GPS Receivers［J］.Chinese Science Bulletin，49（2），196－200.（欧吉坤，王振杰.单频GPS快速定位中模糊度解算的一种新方法［J］.科学通报，2004，49（2）：196－200.）

［4］ GUI Qingming，HAN Songhui.New Algorithm of GPS Rapid Positioning Based on Double－k－type Ridge Estimation［J］.Journal of Surveying Engineering，2007，133（4）：173－178.

［5］ LI Bofeng，SHEN Yunzhong.Prior Baseline Information Based Fast GPS Ambiguity Resolution［J］.Acta Geodaetica et Cartographica Sinica，2008，37（4）：413－417.（李博峰，沈云中.顾及基线先验信息的GPS模糊度快速解算［J］.测绘学报，2008，37（4）：413－417.）

［6］ SHEN Yunzhong，LI Bofeng.Regularized Solution to Fast GPS Ambiguity Resolution［J］.Journal of Surveying Engineering，2007，133（4）：168－172.

［7］ LI Bofeng，SHEN Yunzhong，FENG Yanming.Fast GNSS Ambiguity Resolution as an Ill－posed Problem［J］.Journal of Geodesy，2010，84：683－698.

［8］ FREI E，BEULTER G.Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach‘FARA’：Theory and First Results［J］.Manuscript Geodesy，1990，15：326－356.

［9］ HATCH R.Instantaneous Ambiguity Resolution［C］∥Proceedings of KIS’90.Banff：［s.n.］，1990：299－308.

［10］ PARK C，KIM I，LEE J，et al.Efficient Ambiguity Resolution Using Constraint Equation［C］∥Proceedings of IEEE Position Location and Navigation Symposium.Atlanta：IEEE，1996：277－284.

［11］ LI Bofeng，SHEN Yunzhong.Global Navigation Satellite System Ambiguity Resolution with Constraints from Normal Equations［J］.Journal of Surveying Engineering，2010，136（2）：63－71.

［12］ EULER H，LANDAU H.Fast Ambiguity Resolution On－The－Fly for Real－Time Applications［C］∥Proceeding of 6th International Geodetic Symposia on Satellite Positioning.Columbus：［s.n.］，1992：650－659.

［13］ LI Bofeng，SHEN Yunzhong.An Improved ARCE Algorithm for GPS Ambiguity Resolution［J］.Journal of Geodesy and Geodynamics，2006，26（3）：102－105.（李博峰，沈云中.改进的ARCE算法［J］.大地测量与地球动力学，2006，26（3）：102－105.）

［14］ LI Bofeng，SHEN Yunzhong.Fast GPS Ambiguity Resolution Constraint to Available Conditions［J］.Geomatics and Information Science of Wuhan University，2009，34（1）：117－121.（李博峰，沈云中.附有约束条件的GPS模糊度快速解算［J］.武汉大学学报：信息科学版，2009，34（1）：117－121.）

［15］ LI Bofeng.Theory and Method of Parameter Estimation for Mixed Integer GNSS Stochastic and Function Model［D］.Shanghai：Tongji University，2010.（李博峰.混合整数GNSS函数模型和随机模型参数估计理论与方法［D］.上海：同济大学，2010.）

［16］ HASSIBI A，BOYD S.Integer Parameter Estimation in Linear Models with Applications to GPS［J］.IEEE Transactions on Signal Processing，1998，46（11）：2938－2952.

［17］ TEUNISSEN P.Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping［J］.Journal of Geodesy，1998，72：606－612.

［18］ TEUNISSEN P.The Parameter Distributions of the Integer GPS Model［J］.Journal of Geodesy，2002，76：41－48.

［19］ VERHAGEN S.The GNSS Integer Ambiguities：Estimation and Validation［D］.Delft：Delft University of Technology，2005.

［20］ XU Peiliang.Voronoi Cells，Probabilistic Bounds and Hypothesis Testing in Mixed Integer Linear Models［J］.IEEE Transaction Information Theory，2004，52（2）：3122－3138.

［21］ ZHU L，LAI Y，SHAH M，et al.Efficiency of Carrierphase Integer Ambiguity Resolution for Precise GPS Positioning in Noisy Environments［J］.Journal of Geodesy，2007，81：149－156.

［22］ DE JONGE P，TIBERIUS C.The LAMBDA Method for Integer Ambiguity Estimation：Implementation Aspects［R］.Delft：Delft Geodetic Computing Centre，1996.

［23］ DONG D，BOCK Y.Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California［J］.Journal of Geophysical Research，1989，94：3949－3966.

［24］ TEUNISSEN P，SIMONS D，TIBERIUS C.Probability and Observation Theory［R］.Delft：Delft University of Technology，2008.

E－mail：bofeng＿li＠163.com

Error Probability Controllable Integer Rounding Method and Its Application to RTK Ambiguity Resolution

LI Bofeng1，SHEN Yunzhong2，ZHANG Xingfu3
1.Key Laboratory of Advanced Surveying Engineering of SBSM，Tongji University，Shanghai 200092，China；2.College of Surveying and Geo－informatics，Tongji University，Shanghai 200092，China；3.Department of Surveying and Geomatics，Guangzhou University of Technology，Guangzhou 510006，China

RTK ambiguity resolution is usually preferable to sequential rounding method to partially fix the ambiguities that can be fixed with high reliability.Hence，it is crucial to control the error probability of rounding.The issue of reliable rounding based on the theory of multiple hypothesis testing will be addressed，where the rounding interval is adaptively determined in terms of the user－defined critical level to tightly control the error probability of ambiguity fixing.Furthermore，regarding to the two special scenarios in real GNSS applications，two easy－to－use rounding strategies are developed.The dual－frequency GPS data collected from two CORS stations of 94.6 km baseline is carried out as a network RTK ambiguity resolution instance to evaluate the performance of the proposed new rounding strategies.The results show that，comparing with the ordinary rounding strategies，the new rounding strategies can indeed control error probability of ambiguity fixing whilst keeping the moderate fix－rate.

RTK；integer rounding；type II error；multiple hypotheses；hypothesis testing

LI Bofeng（1983—），male，postdoctoral fellow，majors in geodetic data processing theory，GNSS theory and applications.

LI Bofeng，SHEN Yunzhong，ZHANG Xingfu.Error Probability Controllable Integer Rounding Method and Its Application to RTK Ambiguity Resolution［J］.Acta Geodaetica et Cartographica Sinica，2012，41（4）：483－489.（李博峰，沈云中，张兴福.纳伪概率可控的四舍五入法及其在RTK模糊度固定中的应用［J］.测绘学报，2012，41（4）：483－489.）

P228

A

1001－1595（2012）04－0483－07

国家自然科学基金（41074018；41104002）

宋启凡）

2011－09－29

2011－12－06

李博峰（1983—），男，博士后，研究方向为大地测量数据处理理论，GNSS理论与应用。