顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化

李姗姗，吴晓平，张传定，欧阳永忠

1.信息工程大学测绘学院，河南郑州450052；2.海军海洋测绘研究所，天津300061

顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化

李姗姗1，吴晓平1，张传定1，欧阳永忠2

1.信息工程大学测绘学院，河南郑州450052；2.海军海洋测绘研究所，天津300061

推证顾及地形与完全球面布格异常梯度改正的完全到一阶项的物理大地测量边值问题的严密解式，并在某试验区综合利用地形、重力、GPS／水准等数据进行区域似大地水准面的计算与检验。通过对高程异常计算绝对与相对精度的比较分析，结果表明，完全球面布格异常梯度改正项对高程异常的影响能够达到厘米的量级。因此，提高区域似大地水准面的建模精度，尤其是在地形起伏较大的区域，除需顾及地形改正项影响外，还应考虑完全球面布格异常梯度改正项对高程异常的影响。

似大地水准面；地形改正；完全球面布格异常梯度；奇异积分；高程异常

1 引 言

似大地水准面是我国高程系统的一个基准面，目前可提供使用的2000中国重力场与似大地水准面模型（CGGM2000），其绝对精度在我国东部地区优于±0.2m，西部地区优于±0.3m，并保持了陆地和近海区域重力场与大地水准面的整体性。然而随着卫星、航空、海洋、陆地重力测量技术的发展与成熟，地面重力数据覆盖的密度与均匀度越来越高，因此为了进一步提高区域大地水准面建模的绝对与相对精度，以满足工程上的应用需求，有必要对基于Molodensky理论求解地球重力场的严密理论、方法以及实现进行深入研究，从而才有可能实现“GPS＋似大地水准面模型”技术，快速为用户提供厘米级精度的正常高。

似大地水准面精化问题一直以来都是我国物理大地测量学者致力研究的热点。文献［1—3］利用地球重力场“可叠加性”的特性以及我国GPS／水准、重力、地形以及全球重力场模型，采用均衡理论进行重力归算与内插外推，采用球面一维FFT计算技术、基于Stokes和顾及G1项的Molodenskey公式，并顾及椭球改正，建立了我国分米级的（似）大地水准面模型；文献［4］利用高精度重力、地形、高阶地球重力场模型和GPS／水准数据，采用严密的球面核函数和1D－FFT技术，建立了我国深圳市1km分辨率的厘米级大地水准面模型；文献［5］研究探讨了在已知厘米级精度地球重力场位系数模型、地形密度分布模型以及平均海面高模型的前提下，基于虚拟压缩恢复理论实现全球1°×1°厘米级精度大地水准面的方法；文献［6］研究分析了基于二维平面和二维球面FFT计算大地水准面算法的特点以及差异，并利用改进后的数学模型对我国海陆大地水准面进行了计算与精度评定；文献［7］提出了为满足高精度局域大地水准面的建模要求，在不同地形区域对GPS水准网精度与密度的布设要求。

在实际基于高分辨率、高精度的重力数据、高分辨率数字地面模型（digital terrain model，DTM）以及全球重力场模型计算高程异常时，一般采用移去－恢复技术［8］，且认为Molodenskey一阶解等价于地形改正项影响，假设的前提是重力异常与地形成线性关系［9－10］。然而在地形起伏较大的区域，重力异常与地形之间并不严格成线性关系。针对这一问题，本文在上述研究的基础上，在顾及一阶项的Molodenskey理论计算重力似大地水准面方面作相应研究，推导建立其严密解式，并利用某试验区数据进行计算分析与精度评定。

2 完全到一阶项的联合重力和地形数据确定高程异常的解式

球近似意义下，Δg与外部扰动位T的关系为［11］

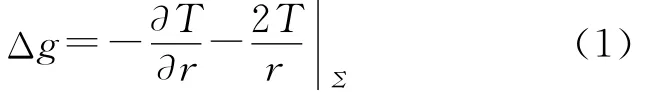
式中，Σ为地球自然表面，其上的重力异常值为Δg。若以似大地水准面（或大地水准面）为界将扰动位分为两个部分，分别以Ti表示其内部扰动质量的位，Te表示外部地形质量的位。相应的，Σ面上的重力异常也可分解为两个部分Δgi和Δge，即

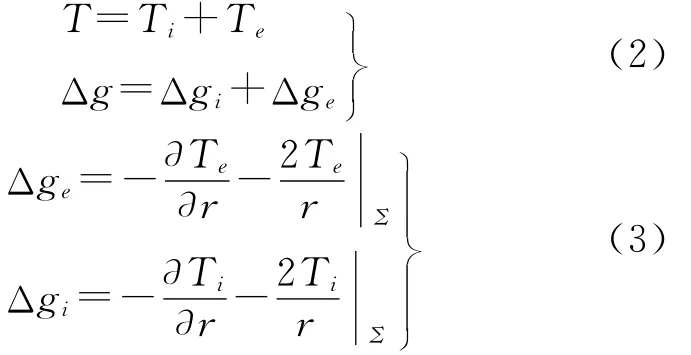
对于外部地形物质位，可表示为

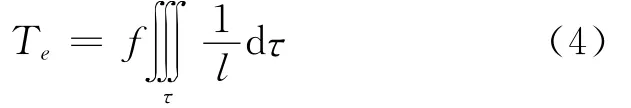
若只取通常的球近似，也就是说，用一个半径为R的球来代替似大地水准面，则上式积分区域为似大地水准面之外（R≤r≤R＋h）；dτ是体积单元，设点P是计算地形位的点，则l是dτ至P点的距离；ρ是地形质量的密度，式中已假定为常数2.67gcm－3，略去h／R≤0.14%的影响，则地形物质的位就变为

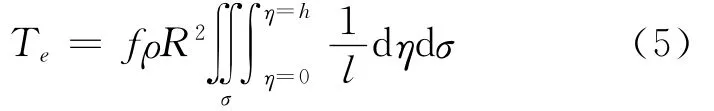
式中，对于dσ的积分，表示对整个立体角积分，而

它表示积分dτ的海拔高（球近似意义的海面也是指r＝R的球面）。将式（5）分解为两个部分，完成积分可将地形质量的位表示为

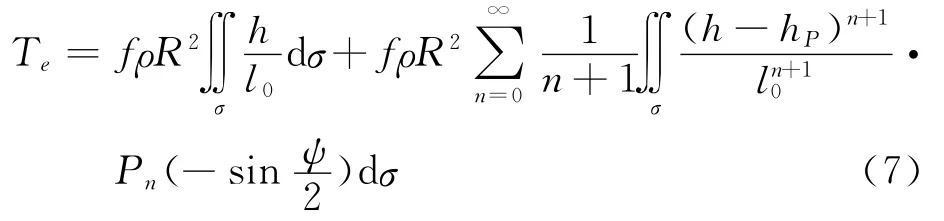
地形物质的垂直引力是地形物质位的径向方向导数的负值［12］，即

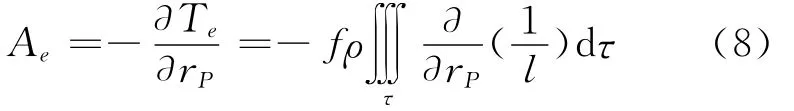
又

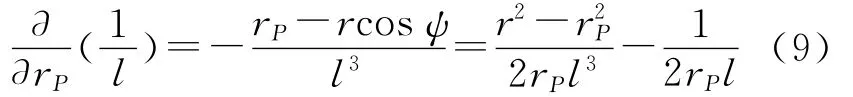
代入式（8），得

并有

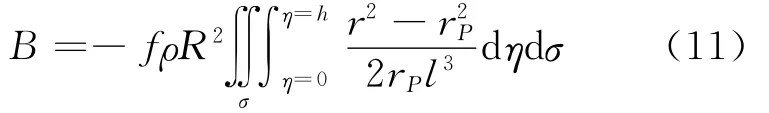
与式（5）比较，也可以将其分解为相应的两项，分别完成积分后，得

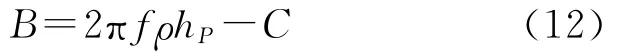
式中，C为球面近似地形改正［13－15］

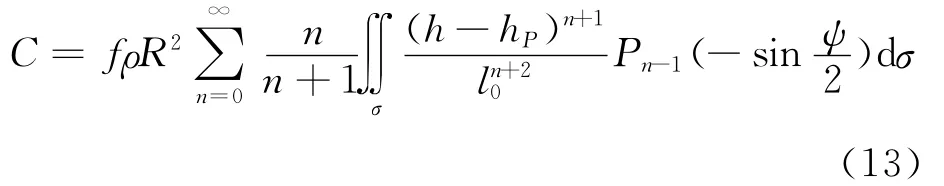
将式（12）代入式（10），得

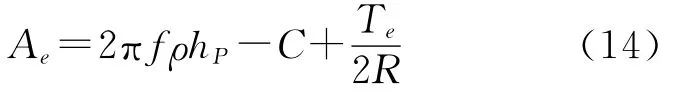
式（14）代入式（3），得

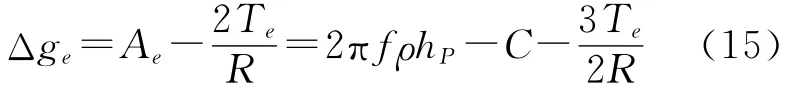
由式（2）和式（15），得

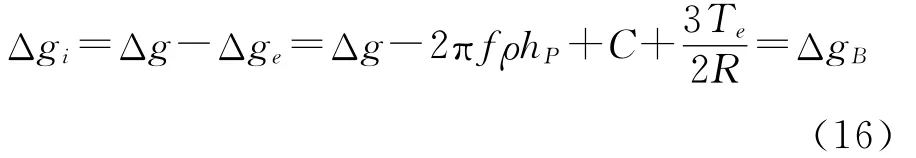
为完全球面布格异常。由于完全球面布格异常不仅扣除了地形物质引力的影响，而且也扣除了地形位的影响；与平面布格异常相比，进一步消除了地形有关的高频部分［16］，因而其变化更加平缓，值得在实践中采用。

剩下的问题是如何确定计算点处的（Ti）A。对于线性地面边值问题，一般都是作为固定边值问题处理，即过计算点A的重力位水准面W＝WA是一个物理曲面，同时也可作为一个几何曲面来看待。在减去地形物质产生的重力异常Δge之后，则可视似大地水准面外已没有质量存在。此时Ti在似大地水准面外是调和的，并且该扰动位对应的重力异常在Σ面上的值Δgi也是已知的。这样的边值问题可解释为重力在Σ面上进行测量，确定Σ上的扰动位Ti的问题。其解可依照Moritz的解析延拓理论［8］，将Σ面上P点处的（Δgi）P解析延拓到移动地形物质前的过A点的水准面W＝WA上（这时可视为几何曲面，是固定界面）的P0点，则

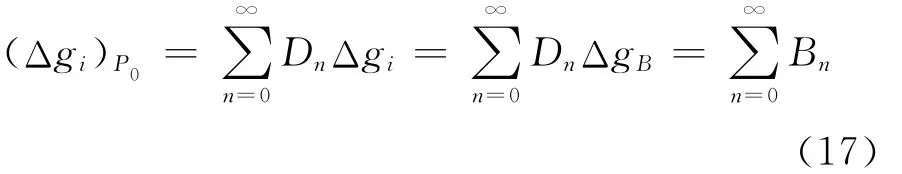
式中

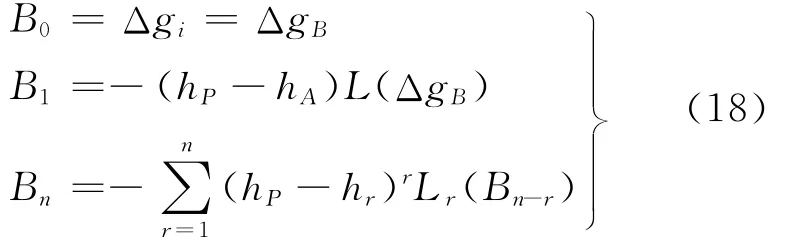
扰动位Ti在A点处的值为

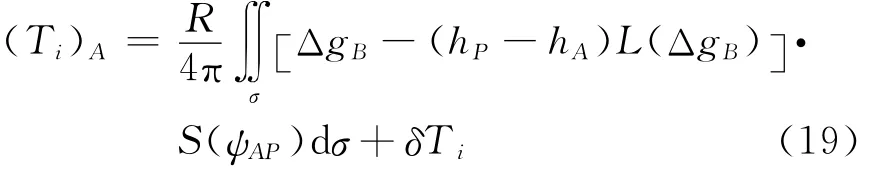
式中

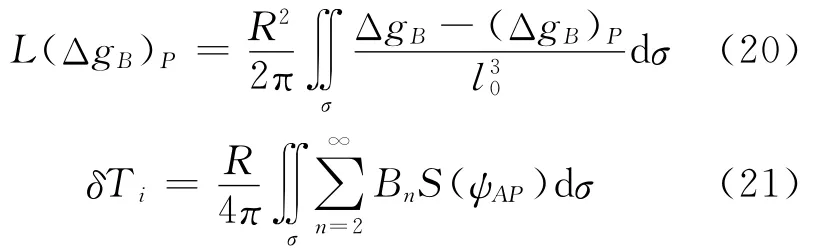
将式（7）和式（19）相加直接写出联合地形和地面重力异常数据确定地面扰动位的基本公式

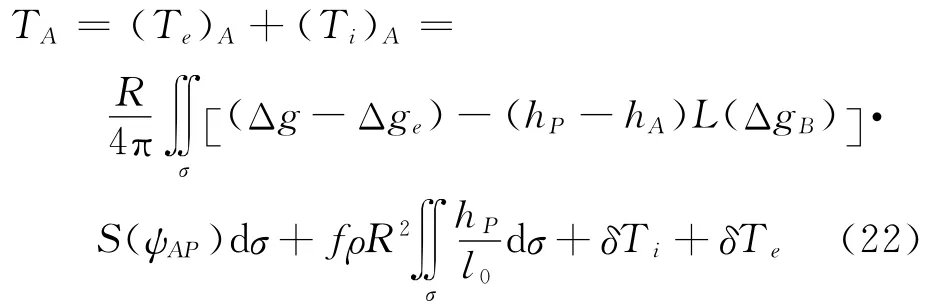
式中

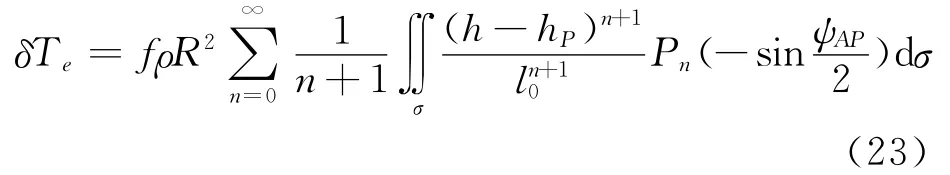
式（22）这一解式，各项物理意义明晰，但是每个量的计算都是一个全球积分，在进行实际数据处理时，除了地形高数据和重力异常数据密度不匹配会引进很大的附加误差外，还存在布格改正直接、间接影响量级很大，相互抵偿后也会引进计算误差。为此，利用球近似下恒等式［17］

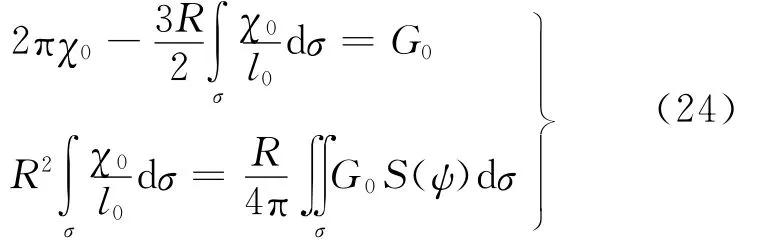
取χ0＝fρh，并顾及式（7）、（15）和（23），则可得到

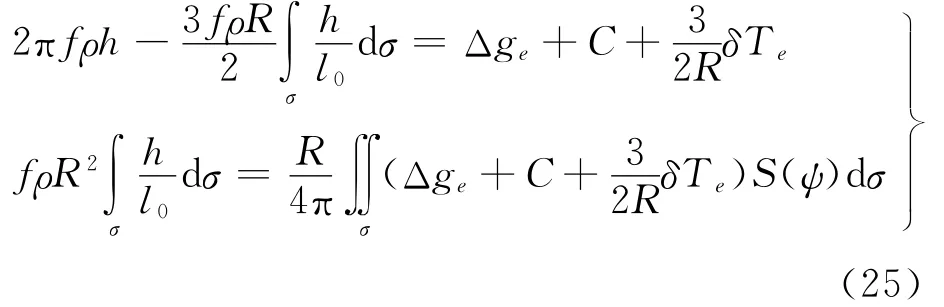
利用式（25）的第2个等式，可将式（22）简化为

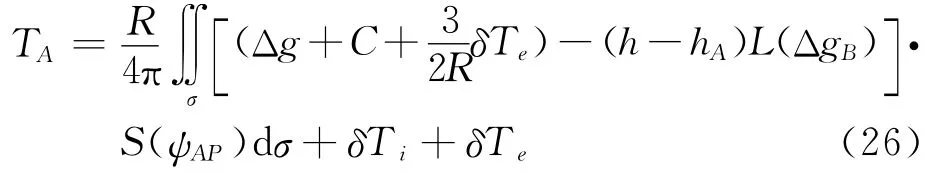
至此，可以看出，基于球面布格异常所得球面地形改正解的主项是前述空间异常与高程成线性关系时的地形改正解，再加上空间异常与高程异常非线性部分的改正项和所有地面边值问题解中都要涉及的高阶改正项，这里为δTe＋δTi。

最后略去式（26）的高阶项，由布隆斯公式得到联合地形和重力异常数据确定似大地水准面的公式

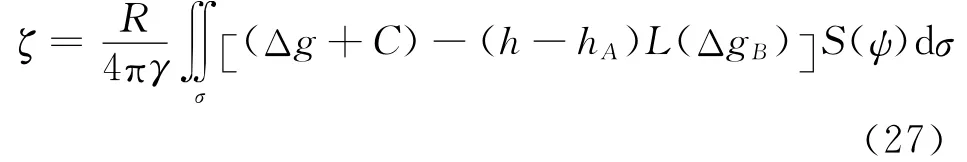
3 完全球面布格异常梯度计算

在实际计算应用过程中，一般将积分区域分为内区σ0和外区σ－σ0影响，并视内区近似为平面，因此式（20）可表示为

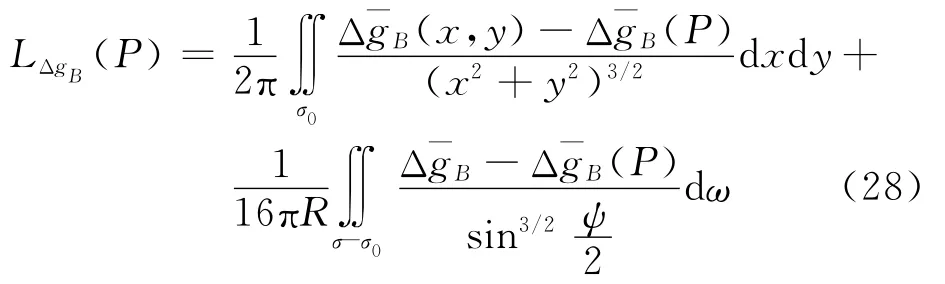
为解决内区中的奇异积分，在计算点附近中心引入重力异常双二次曲面拟合模型［18－20］

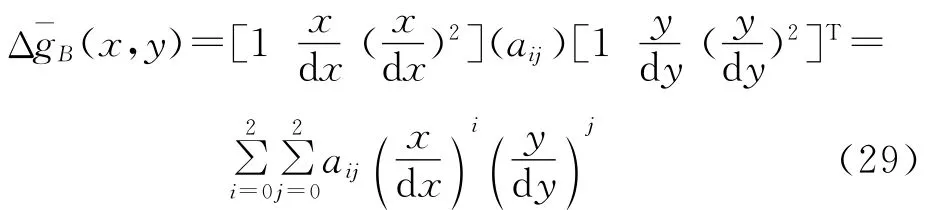
则中心区非奇异计算公式为

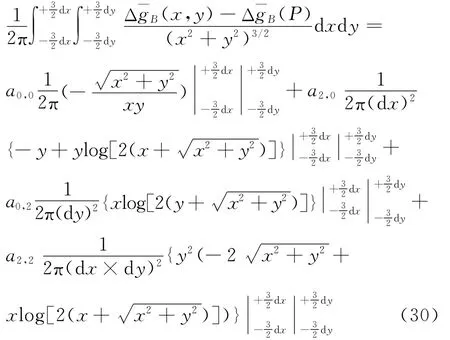
由于外区影响与距离的立方成反比，因此外区积分只需取至一定的积分半径区域范围，此时积分变为累加求和的形式

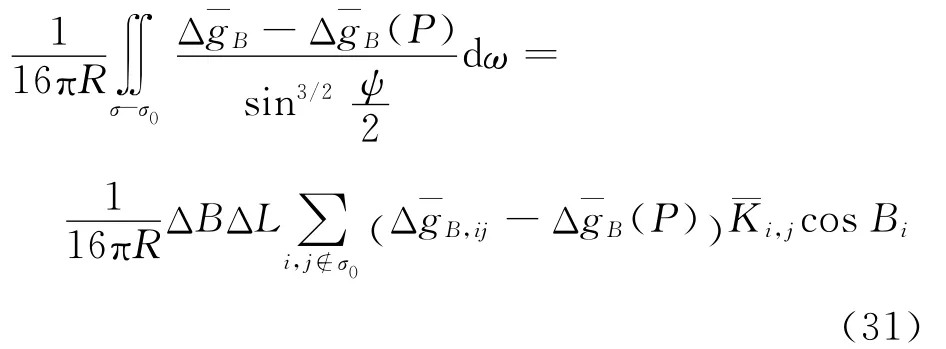
选定某试验区，该区域重力异常与高程数值变化大小如图1、2所示，数据分辨率均为1′×1′，按照上述公式计算得到了该试验区完全球面布格异常垂向梯度，结果如图3所示，并计算了该区域重力异常的垂向梯度，如图4，两者数值统计比较结果如表1所示。

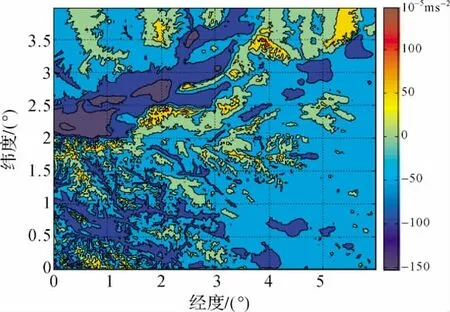
图1 试验区重力异常Fig.1 Gravity anomalies in the experiment area

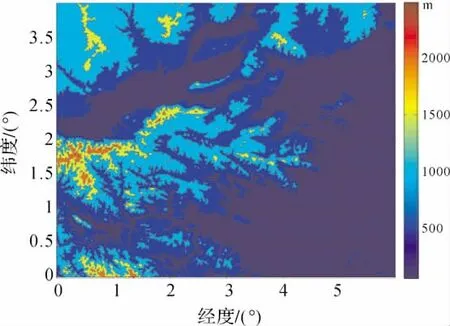
图2 试验区高程Fig.2 Heights in the experiment area

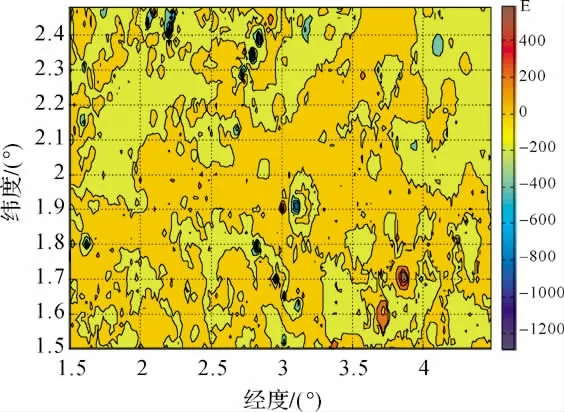
图3 完全球面布格异常垂向梯度Fig.3 Vertical gradient of complete spherical Bouguer anomalies

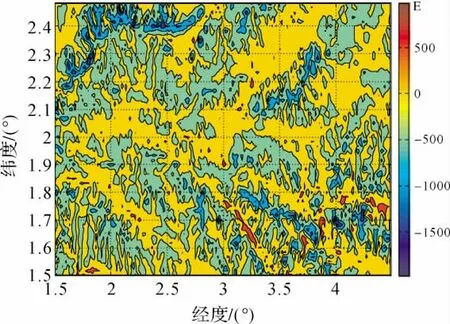
图4 重力异常垂向梯度Fig.4 Vertical gradient of gravity anomalies

表1 重力异常与完全球面布格异常的垂向梯度的统计Tab.1 Statistics of vertical gradients of gravity anomalies and complete spherical Bouguer anomalies E

从图3、图4可以看出，完全球面布格异常垂向梯度L（ΔgB）较之于重力异常垂向梯度L（Δg）的变化要平缓得多，表1的统计结果也反映出重力异常垂向梯度L（Δg）比完全球面布格异常垂向梯度L（ΔgB）的变化幅度大一个数量级。显然，这是由于重力异常与地形的相关性较强，而扣除了地形相关部分所得的完全球面布格异常的垂向梯度的量级较小，便于实际数值的内插、外推以及归算等应用计算。进一步将完全球面布格异常及其垂向梯度与完全平面布格异常及垂向梯度进行比较，结果如图5、图6所示。

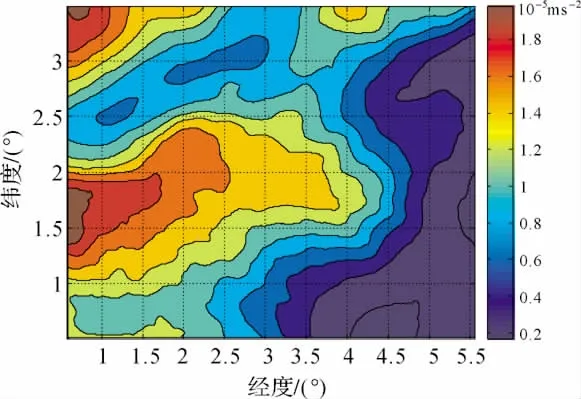
图5 两者异常差值Fig.5 Difference between the two types of Bouguer anomalies

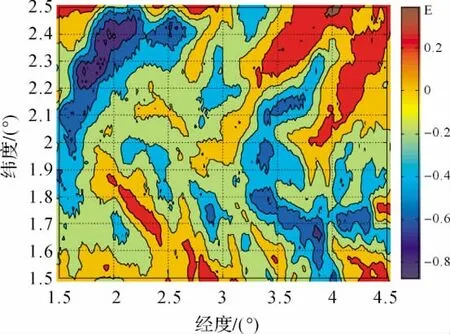
图6 两者垂向梯度差值Fig.6 Vertical gradient difference between the two types of Bouguer anomalies

表2 两者及其垂向梯度差值的统计Tab.2 Statistics of difference and vertical gradient difference between the two types of Bouguer anomalies

从表2两者差值的统计结果可以看出，完全球面布格异常与完全平面布格异常相比，量级上的变化大概在几个毫伽左右，垂向梯度数值上的变化并不明显，用完全平面布格异常梯度替代完全球面布格异常梯度项对大地水准面所产生的影响在目前测量水平的基础上可以忽略。然而实现完全球面布格异常以及梯度项计算，一是从理论上而言更趋于严密，二是随着计算机性能水平的提高，计算速度已不是问题，寻求更准确、更精细地确定地球重力场元将是未来的发展趋势。

4 完全球面布格异常梯度改正项对高程异常的影响

地形改正C在线性边值问解中的作用已被认可，本节主要探讨完全球面布格异常梯度改正g1项（g1＝－（h－hA）L（ΔgB））对高程异常的影响，并与地形改正C的作用相比较。该试验区地形改正C和g1项对高程异常影响的计算结果如图7、图8所示，统计结果如表3所示。

图7 地形改正对高程异常的影响Fig.7 Effect on height anomaly by terrain correction

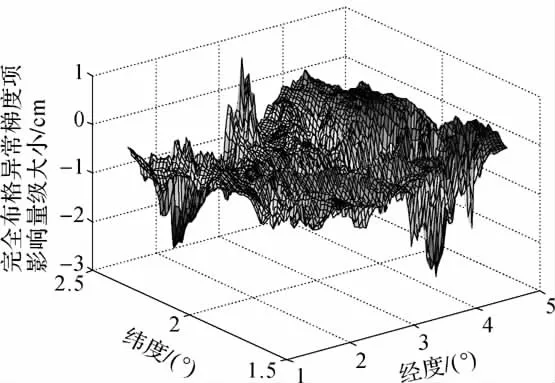
图8 g1项对高程异常的影响Fig.8 Effect on height anomaly by g1term

表3 地形改正与g1项对高程异常的影响Tab.3 Effect on height anomaly by terrain correction and g1term cm

从表3中可以看出，g1项对高程异常的影响也可达到几个厘米。这些数值结果也说明边值问题的地形改正项与完全球面布格异常所引起的梯度改正项在某些区域能达到同等的量级。若同时顾及这两项改正，可达到取至一阶项解析延拓解的精度。

进一步探讨该试验区完全球面布格异常与完全平面布格异常梯度改正项对高程异常计算结果的影响，从图9和表4可以看出两者对高程异常计算结果影响的量级基本相当，但实践中编程计算速度并无明显区别，因此从理论的严密程度来看，建议在计算高程异常时采用完全球面布格异常梯度改正项。

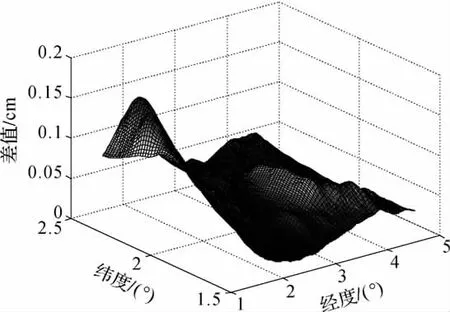
图9 完全球面与完全平面布格异常梯度改正项对高程异常计算结果影响的差值Fig.9 Difference between the height anomaly calculation results considering complete spherical and complete plane Bouguer anomaly’s gradient terms separately

表4 完全球面布格异常梯度改正项与完全平面布格异常梯度改正项对高程异常计算结果的差值统计Tab.4 Statistics of difference between the height anomaly calculation results considering complete spherical and complete plane Bouguer anomaly’s gradient terms separately cm

采用EGM2008地球重力场模型，基于移去－恢复技术，计算了图1试验区1′×1′的重力高程异常值（未加完全球面布格异常梯度改正项计算的格网高程异常值，加了完全球面布格异常梯度改正项计算的格网高程异常值）。为了评定两者的计算精度，利用该试验区范围内的20个GPS水准点作为真值，按插值方法由格网高程异常值分别推求出20个点的高程异常计算值，二者之差作为真误差，得到它们的中误差如表5所示。

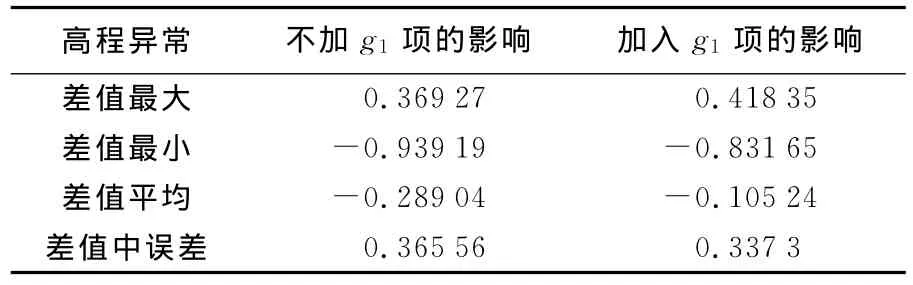
表5 重力高程异常的计算精度Tab.5 Calculation precision of gravity height anomaly m

从表5中误差的数值可以看出，顾及完全球面布格异常梯度改正项，能提高高程异常的计算精度。此外统计40km左右区域范围内的相对高程异常差，以GPS水准两点之间的高程异常差作为真值，并分别计算加入g1项与不加入g1项的高程异常差，与GPS水准高程异常差求差进行精度评定，统计结果如表6所示。

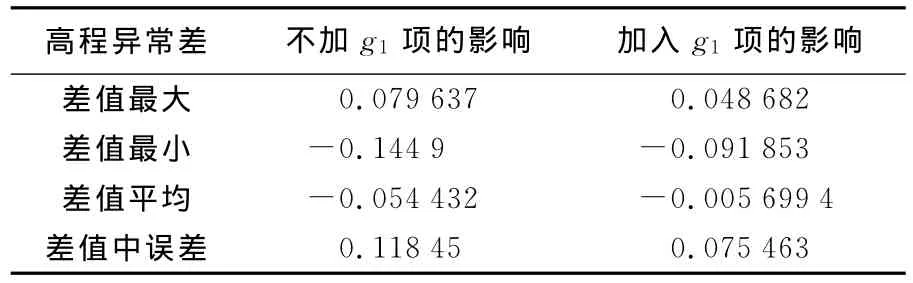
表6 重力高程异常差的计算精度Tab.6 Calculation precision of gravity height anomaly difference m

显然顾及地形改正及其完全球面布格异常梯度改正项的影响，高程异常相对计算精度能够达到厘米级水平。

5 结 论

区域厘米级似大地水准面的建立是物理大地测量的重要工作之一。随着测量技术的日益发展，重力及地形数据的覆盖日趋密集与均匀，因而对重力场数据处理方法也要求尽可能严密，并能得以工程化实现。本文推导了完全到一阶项的联合重力和地形数据确定高程异常的解式，并在某试验区进行了计算比较，数值结果表明：① 完全球面布格异常垂向梯度较之于空间异常垂向梯度的数值量级要小得多，说明了完全球面布格异常变化平缓，更适宜于实践中重力场的内插、外推以及重力数据归算等工作；② 顾及地形改正及其完全球面布格异常梯度改正项的影响，与仅考虑地形改正项相比能提高高程异常建模的绝对精度，同时相对高程异常的计算精度能够达到厘米级水平。

［1］ CHEN Junyong，LI Jiancheng，NING Jinsheng，et al.On a High Resolution and High Accuracy Geoid in China Mainland［J］.Acta Geodaetica et Cartographica Sinica，2001，30（2）：95－100.（陈俊勇，李建成，宁津生，等.我国大陆高精度、高分辨率大地水准面的研究和实施［J］.测绘学报，2001，30（2）：95－100.）

［2］ CHEN Junyong，LI Jiancheng，NING Jinsheng，et al.On a Chinese New Quasi Geoid［J］.Acta Geodaetica et Cartographica Sinica，2002，31（Sup.）：1－6.（陈俊勇，李建成，宁津生，等.中国似大地水准面［J］.测绘学报，2002，31（增刊）：1－6.）

［3］ CHEN Junyong，LI Jiancheng，NING Jinsheng，et al.A New Chinese Geoid with High Resolution and High Accuracy［J］.Geomatics and Information Science of Wuhan University，2001，26（4）：283－289.（陈俊勇，李建成，宁津生，等.中国新一代高精度、高分辨率大地水准面的研究和实施［J］.武汉大学学报：信息科学版，2001，26（4）：283－289.）

［4］ NING Jinsheng，LUO Zhicai，YANG Zhanji，et al.Determination of Shenzhen Geoid with 1km Resolution and Centimeter Accuracy［J］.Acta Geodaetica et Cartographica Sinica，2003，32（2）：102－107.（宁津生，罗志才，杨沾吉，等.深圳市1km高分辨率厘米级高精度大地水准面的确定［J］.测绘学报，2003，32（2）：102－107.）

［5］ CHAO Dingbo，SHEN Wenbin，WANG Zhengtao.Investigations of the Possibility and Method of Determining Global Centimeter－level Geoid［J］.Acta Geodaetica et Cartographica Sinica，2007，36（4）：370－376.（晁定波，申文斌，王正涛.确定全球厘米级精度大地水准面的可能性和方法探讨［J］.测绘学报，2007，36（4）：370－376.）

［6］ HUANG Motao，ZHAI Guojun，GUAN Zheng，et al.Comments on FFT Technique in Spectral Geoid Determination［J］.Acta Geodaetica et Cartographica Sinica，2000，29（2）：124－131.（黄谟涛，翟国君，管铮，等.利用FFT技术计算大地水准面高若干问题研究［J］.测绘学报，2000，29（2）：124－131.）

［7］ CHEN Junyong.Needs for GPS Leveling Network and Gravimetry in a High Accuracy Local Area Geoid［J］.Acta Geodaetica et Cartographica Sinica，2001，30（3）：189－191.（陈俊勇.高精度局域大地水准面对布测GPS水准和重力的要求［J］.测绘学报，2001，30（3）：189－191.）

［8］ HOFMANN－WELLENHOF B，MORITZ H.Physical Geodesy［M］.Graz，Wien，New York：Springer，2005.

［9］ GUAN Zelin，GUAN Zheng，HUANG Motao，et al.Theory and Method of Reginonal Gravity Field Approximation［M］.Beijing：Surveying and Mapping Press，1997.（管泽霖，管铮，黄谟涛，等.局部重力场逼近理论和方法［M］.北京：测绘出版社，1997.）

［10］ GUO Junyi.Foundation of Physical Geodesy［M］.Wuhan：Wuhan Surveying and Mapping Techonology University Press，1994.（郭俊义.物理大地测量学基础［M］.武汉：武汉测绘科技大学出版社，1994.）

［11］ LU Zhonglian.Theory and Method of the Earth’s Gravity Field［M］.Beijing：PLA Publishing House，1996.（陆仲连.地球重力场的理论与方法［M］.北京：解放军出版社，1996.）

［12］ EMELJANOV N V，KANTER A A.A Method to Compute Inclination Functions and Their Derivatives［J］.Manuscripta Geodaetica，1989，14（2）：77－83.

［13］ FORSBERG R.Gravity Field Terrain Effect Computations by FFT［J］.Journal of Geodesy，1984，59（4）：342－360.

［14］ SCHWARZ K P，SIDERIS M G，FORSBERG R.The Use of FFT Techniques in Physical Geodesy［J］.Geophysical Journal International，1990，100（3）：485－514.

［15］ SIDERIS M G.A Fast Fourier Transform Method of Computing Terrain Corrections［J］.Manuscript Geodaetica，1985，10（1）：66－73.

［16］ LI Shanshan，WU Xiaoping，ZHANG Chuanding，et al.Calculation and Analysis of the New Statistical Character Parameters of Gravity Field in China［J］.Chinese Journal of Geophysics，2010，53（5）：1099－1108.（李姗姗，吴晓平，张传定，等.我国重力场新的统计特征参数的计算分析［J］.地球物理学报，2010，53（5）：1099－1108.）

［17］ LI Jiancheng，CHEN Junyong，NING Jinsheng，et al.Approximation Theory of the Earth Gravity Field and Determination of the Chinese Gravity Geoid Model 2000［M］.Wuhan：Wuhan University Press，2003.（李建成，陈俊勇，宁津生，等.地球重力场逼近理论与中国2000似大地水准面的确定［M］.武汉：武汉大学出版社，2003.）

［18］ ZHU Changqing.Method of Calculation and Application in Surveying and Mapping［M］.Beijing：Surveying and Mapping Press，1988.（朱长青.计算方法及其在测绘中的应用［M］.北京：测绘出版社，1988.）

［19］ WU Zongmin.Model，Method and Theory of Scattering Data Fitting［M］.Beijing：Science Press，2008.（吴宗敏.散乱数据拟合的模型、方法和理论［M］.北京：科学出版社，2008.）

［20］ LI Shanshan，WU Xiaoping，ZHAO Dongming.Coons Curved Surface Reconstruction Method of Marine Gravity Anomaly Map for Navigation［J］.Acta Geodaetica et Cartographica Sinica，2010，39（5）：508－515.（李姗姗，吴晓平，赵东明.导航用海洋重力异常图的孔斯曲面重构方法［J］.测绘学报，2010，39（5）：508－515.）

E－mail：zzy＿lily＠sina.com

Regional Quasi－Geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly’s Gradient Term

LI Shanshan1，WU Xiaoping1，ZHANG Chuanding1，OUYANG Yongzhong2
1.Institute of Surveying and Mapping，Information Engineering University，Zhengzhou 450052，China；2.Naval Research Institute of Surveying and Mapping，Tianjin 300061，China

The rigorous formulae of the boundary value problem（BVP）of physical geodesy complete to the first－order solution were derived considering corrections of terrain and complete spherical Bouguer anomaly’s gradient term.The formulae were tested through computation of a regional quasi－geoid based on terrain，gravity and GPS／leveling observations within a selected experiment area.Comparison and analysis of the calculated height anomalies in term of absolute and relative accuracy show that the effect of complete spherical Bouguer anomaly’s gradient term on height anomaly could reach centimeter level.Therefore，besides the effect of terrain corrections，the effect of complete spherical Bouguer anomaly’s gradient term on height anomaly should also be taken into account in order to improve the accuracy of regional quasi－geoid modeling especially in areas with rolling terrain.

quasi－geoid；terrain correction；complete spherical Bouguer anomaly’s gradient；singular integral；height anomaly

LI Shanshan（1970—），female，PhD，professor，majors in physical geodesy.

LI Shanshan，WU Xiaoping，ZHANG Chuanding，et al.Regional Quasi－Geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly’s Gradient Term［J］.Acta Geodaetica et Cartographica Sinica，2012，41（4）：510－516.（李姗姗，吴晓平，张传定，等.顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化［J］.测绘学报，2012，41（4）：510－516.）

P223

A

1001－1595（2012）04－0510－07

国家自然科学基金（41174026）；国家重大科学仪器设备开发专项（2011YQ12004503）

宋启凡）

2011－11－22

2012－02－08

李姗姗（1970—），女，博士，教授，研究方向为物理大地测量。