同时估计电离层延迟的单频精密单点定位方法

阮仁桂，吴显兵，冯来平，王夕伟

1.西安测绘研究所，陕西西安710054；2.78155部队，四川成都610036

同时估计电离层延迟的单频精密单点定位方法

阮仁桂1，吴显兵1，冯来平1，王夕伟2

1.西安测绘研究所，陕西西安710054；2.78155部队，四川成都610036

提出一种基于单频码和相位观测量的单频精密单点定位方法，将每个观测量的电离层延迟量与接收机钟差、对流层天顶延迟、接收机位置、相位模糊度一起作为未知参数。采用约化参数的平方根信息滤波与平滑算法进行参数解算。该方法适用于实时定位和事后处理，且不需要外部的电离层模型。采用全球分布的32个IGS监测站16 d实测数据进行静态解算试验，结果表明E、N、U方向的RMS分别为0.023 m、0.018 m、0.059 m；基于一组机载GPS数据进行动态解算试验，得到E、N、U方向的RMS（与载波相位动态相对定位结果比较）分别为0.168 m、0.151 m、0.172 m。

单频精密单点定位；电离层；延迟估计；参数约化；平方根信息滤波；平方根信息平滑

1 引 言

GPS用户市场主要采用的是单频接收机，许多应用领域都对基于单频接收机的精密单点定位非常关注。与双频精密单点定位相比，提高单频精密单点定位精度最大的困难在于电离层延迟改正。过去的几年里，许多学者都进行了单频精密单点定位研究［1－7］，重点就是如何更好地消除电离层延迟的影响。

目前已有多种有效的单频精密单点定位电离层改正方法。最简单也最传统的方法是采用电离层模型改正。GPS导航电文广播的Kloubchar模型只能消除50%～60%的电离层延迟，IGS分析中心等机构提供的基于全球监测网的事后全球电离层格网数据，其精度在2TECU左右（1 TECU引起的L1载波延迟约为0.163m）［8］，但在电离层活动剧烈的区域，其精度难以保证。另一种方法是采用码和相位组合消除电离层延迟。根据电离层引起的群延迟和相延迟大小相等方向相反这一特点，文献［9］首先提出采用GRAPHIC（group and phase ionospheric correction）观测量进行单频电离层延迟改正的方法。文献［4］提出采用GRAPHIC观测量进行低轨卫星定轨的方法，基于单频星载接收机实现1.5m的定轨精度。该方法最大的优点是与电离层模型无关，且模型简单，但是由于模糊度与接收机钟差的相关性，无法获得有意义的钟差估值。另外在单历元情况下，无法同时求解模糊度和位置参数。第3种方法是将电离层延迟作为未知参数进行估计。文献［1］提出在单频精密单点定位中，同时估计电离层天顶延迟及其变率的方法；文献［8］提出了同时估计电离层延迟天顶延迟和水平梯度参数的方法；涂锐分析比较了采用不同映射函数估计电离层延迟的单频精密单点定位结果［10］。这种“天顶延迟＋水平梯度＋映射函数”来表示电离层活动，其模型过于简单。

本文借鉴了估计电离层延迟的思想，提出一种新的单频精密单点定位观测模型和有效的参数估计方法。采用全球分布的32个IGS监测站16d数据和一组机载GPS动态数据进行解算试验，分析算法的精度。

2 观测方程

假设某一单频接收机观测到卫星i的码和相位观测值表示为［11－12］

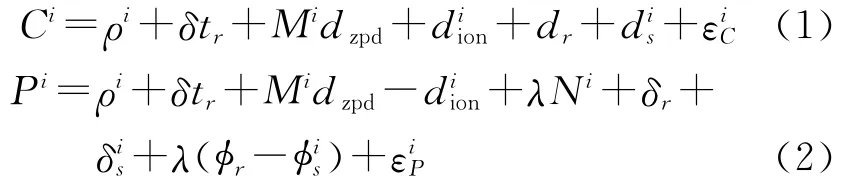
式中，Ci、Pi对应卫星i的码和相位观测量；ρi为接收机到卫星i的几何距离；δtr为接收机钟差；Mi为对流层延迟投影函数；dzpd为对流层天顶延迟；为卫星i的电离层延迟；dr、为接收机和卫星i的码硬件延迟；δr、δis为接收机和卫星i的相位硬件延迟；φr、为接收机和卫星i的初始相位；λ为载波波长；Ni为卫星i的相位整数模糊度、为卫星i的码和相位的观测噪声，包含多路径效应。

考虑设备时延、初始相位、接收机钟差及模糊度等参数之间的相关性，在参数估计时，其中一些参数难以分离，将叠加到一起。重写公式（1）和（2）并整理如下

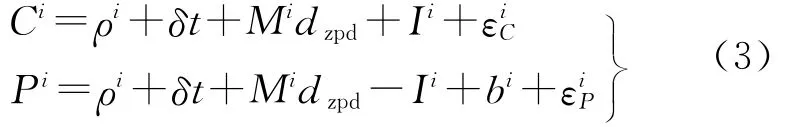
式中，钟差参数δt吸收了接收机设备时延，即δt＝δtr＋dr；电离层路径延迟参数Ii吸收了发射设备时延，即Ii＝＋；bi为模糊度参数，它包含了相位整数模糊度，卫星和接收机的设备时延以及初始相位的影响，即bi＝－dr＋δr＋＋λ（Ni＋φr－）。式（3）的协方差阵为对角矩阵

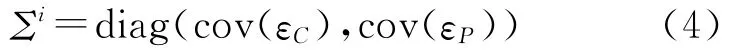
由于接收机钟差、电离层延迟和相位模糊度线性相关，构成的观测方程是秩亏的，在数据处理时可以采用参数约束的方法对模糊度进行约束。

以上公式中没有写出卫星钟差、相对论效应、天线相位中心偏置等改正项，这些改正项可以采用IGS精密数据产品或精确的模型进行改正。文献［13］详细给出了精密单点定位中需要考虑的各种模型改正。

3 滤波模型

假设第k历元观测到m（m＞4）颗卫星，则可得到2×m维观测值向量

未知参数包括接收机钟差δtk，对流层天顶延迟dzpd，k，接收机位置参数xk、yk、zk，模糊度参数b1，b2，…，bm，电离层延迟I1，I2，…，Im。现将未知参数分为两类，表示为

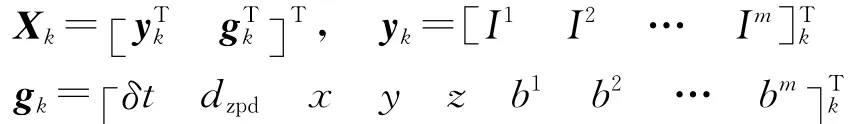
这样，观测方程可写为

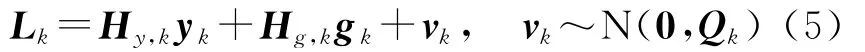
式中

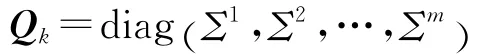
Hg，k和Hy，k是对应未知向量gk和yk的偏导数矩阵。为了方便公式推导，不妨假设Qk＝I（事实上，这一假设可以通过噪声白化的方法实现）［14］。

未知向量gk采用一阶高斯—马尔科夫过程描述

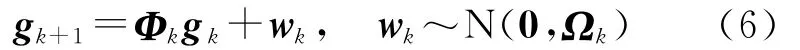
接收机钟差采用白噪声模型，对流层天顶延迟采用随机游走模型，动态定位时，接收机位置采用白噪声模型或随机游走模型，模糊度参数和静态定位时接收机位置作为常量，也可看做是过程噪声为0的随机游走模型。电离层参数向量yk，是普通定位用户不关心的，不对其随时间的变化过程作假设，而是在数据处理时，设法采用参数约化的方法在法方程中逐历元地消去。参数约化的思想在大规模大地网解算和动态数据处理中应用非常普遍［15－18］，本文的数据处理涉及不同类型的参数，在平方根信息滤波与平滑算法［14，19］的基础上作了一些改进，得到带参数约化的平方根信息滤波与平滑算法，基本过程如下。

3.1 观测更新

给定gk初值¯gk及其协方差阵¯Pg，k，令

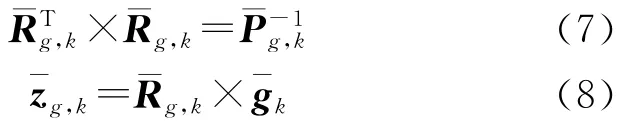
式（9）等号两边同时左乘正交算子Tk，并整理得

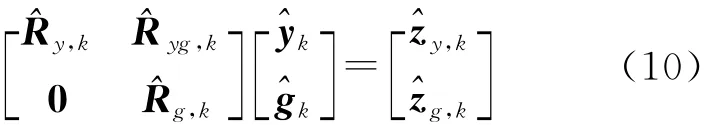
公式（10）可以写为

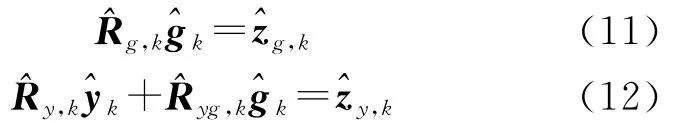
由式（11）可求得

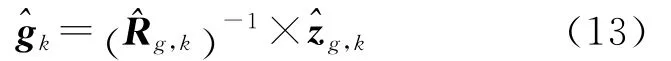
3.2 时间更新

将式（6）写为

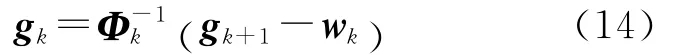
将式（14）代入式（11），联合式（15）可得

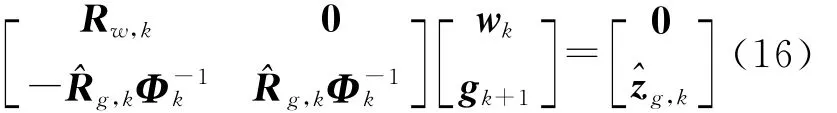
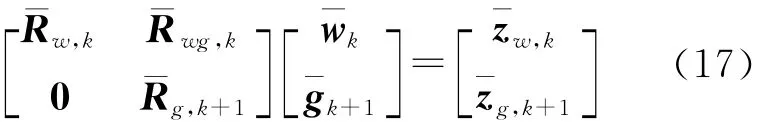
由式（17）可得

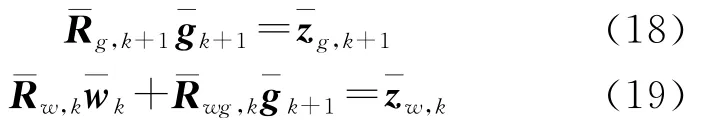
对比式（18）和式（8），注意到已完成状态更新。对于实时定位用户，重复由式（9）、（10）、（13）、（16）和（17）构成的过程，就可逐历元地完成参数约化和平方根信息滤波。

3.3 后向平滑

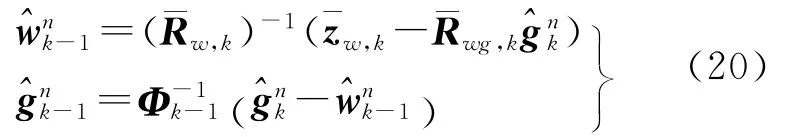
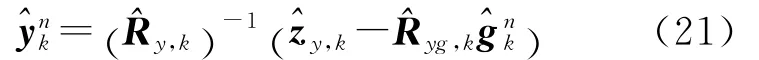
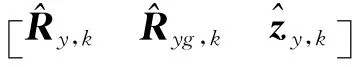
在数据处理中还针对模糊度参数的变化，采用了灵活的变参数技术，使得方程中模糊度参数的个数始终等于当前的有效卫星个数，具体算法和公式推导见文献［20］。正交算子Tk可以通过Givens变换或Householder变换求得［14，19］。

4 试验分析

为了分析算法的精度，采用静态和动态的实测GPS数据进行计算试验。码和相位分别按噪声0.3m和0.002m定权。根据高精度GNSS数据处理的经验，考虑到接收机可能存在钟差跳变，钟差初值取0.0m，初始方差为10－16m2，过程噪声取1012m2；对流层延迟初值取0.0m，初始方差设为0.025m2，过程噪声功率谱密度取5×10－10m2／s；动态定位时接收机位置采用随机游走模型，过程噪声功率谱密度设为104m2／s；模糊度初始值由相位和码观测值相减求得，先验误差设为1000m。

4.1 静态定位试验

收集全球分布的32个IGS观测站2011－03－16（年积日75）到2011－03－31（年积日90）16d的观测数据进行解算试验。这些测站都装备了测量型双频接收机，可获得双频载波相位和P码观测量，以下试验仅使用L1频率上的码和相位观测量。图1为所用测站的分布图，其中近一半的测站处在电离层活动比较剧烈的中低纬度地区（±30°以内），可以充分反映不同电离层活动的影响。

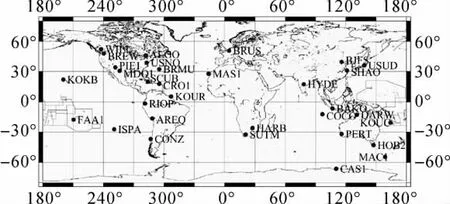
图1 测站分布图Fig.1 Station distribution

利用本文算法，对各测站的单天观测数据进行静态定位解算，将解算结果与已知坐标比较，转换到E、N、U方向的差值表示定位误差。图2是按天统计的静态定位结果E、N、U方向的RMS，可以看出，E和N方向的RMS在0.02m左右浮动，N方向的RMS要略小于E方向。U方向的RMS要明显比E和N方向大一些，约为0.06m。

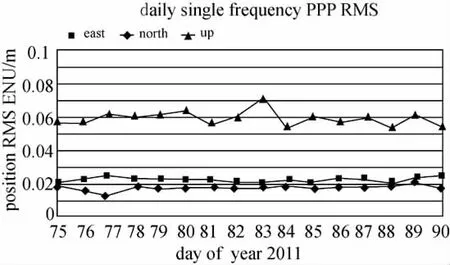
图2 按天统计的静态定位在E、N、U方向的RMSFig.2 Daily static positioning RMS in E，N，U

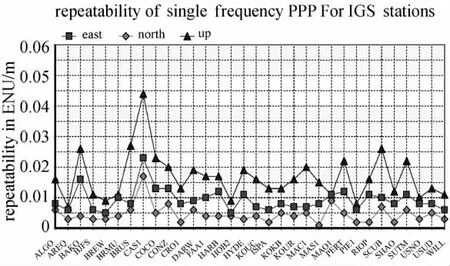
图3 各测站E、N、U方向的重复精度Fig.3 Repeatability in E，N，U w.r.t.stations

图3统计各测站定位结果E、N、U方向的重复精度。多数测站E和N方向的重复精度在0.01m左右，U方向的重复精度优于0.02m。CAS1站的重复精度最差，E、N、U方向分别为0.023m、0.017m和0.044m，综合各测站统计得E、N、U方向的重复精度分别为0.010m、0.005m和0.018m。图4按测站统计了定位结果E、N、U方向的RMS。E和N方向都不超过0.08m，多数测站在0.03m以下；U方向的RMS不超过0.12m，多数测站在0.08m以下。图5统计了各测站定位结果E、N、U方向的最大误差。可以看出E和N方向的误差最大值都不超过0.10m，U方向的最大值不超过0.16m。综合各测站定位结果，统计得到E、N、U方向的RMS分别为0.023m、0.018m和0.059m。

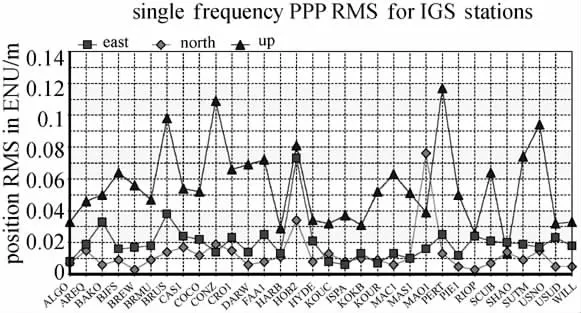
图4 按测站统计的静态定位在E、N、U方向的RMSFig.4 Static positioning RMS in E，N，U w.r.t.stations

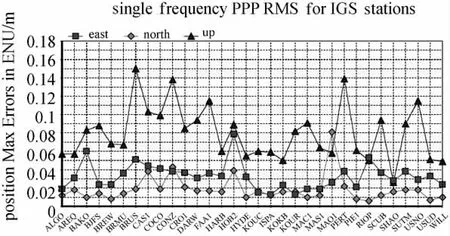
图5 按测站统计的静态定位在E、N、U方向的最大误差Fig.5 Static positioning max errors in E，N，U w.r.t.stations

4.2 动态定位试验

收集2008－09－05的一组机载GPS观测数据进行动态单频精密单点定位试验，数据记录从GPS时3：57：00开始，到7：59：00结束，采样间隔为1s。图6给出了飞机的飞行轨迹，三角形标示了基准站的位置。飞机的平均速度约为250km／h，整个飞行过程中飞机到基准站的距离不超过50km。接收机类型为Novatel OEM4，可获得C1、L1、P2和L2观测值，提取C1和L1观测数据，采用本文的方法进行单点定位解算。将定位结果与grafnav软件的载波相位动态相对定位结果比较得到E、N、U 3个方向的差值，如图7所示［21］。

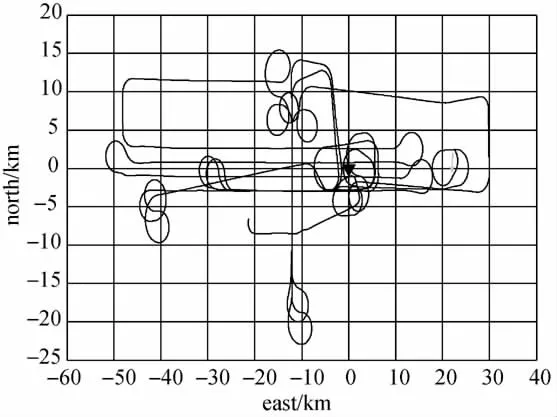
图6 飞机飞行轨迹Fig.6 Trajectory of aircraft

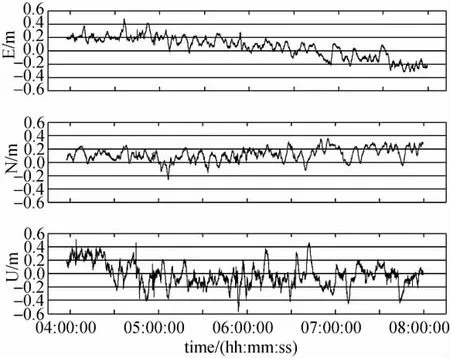
图7 机载数据E、N、U方向定位误差Fig.7 Positioning error in E，N，U with airborne GPS data

可以看出E和N方向的误差都不超过0.5m，U方向误差不超过0.6m。表1统计了机载数据动态定位E、N、U方向和三维位置误差的RMS和最大值（max），可以看出3个方向的RMS都不超过0.2m，三维位置RMS也小于0.3m。

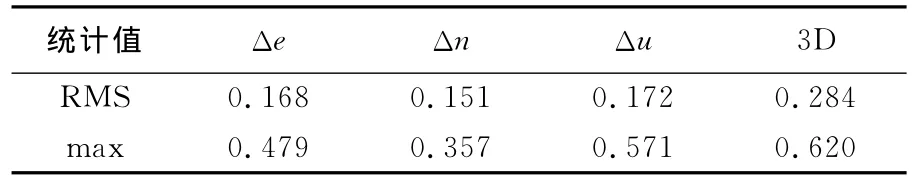
表1 动态定位E、N、U方向和三维RMS的最大误差Tab.1 Kinematic positioning RMS and max errors in E，N，U and 3D m

5 结 论

本文提出一种新的单频精密单点定位方法。基于本文提出的方法，采用单频接收机实现厘米级的静态定位精度和分米级的动态定位精度是有可能的。另外新方法还具有以下优点：

（1）不需要电离层模型，避免了传统的采用模型改正的单频精密单点定位精度受电离层模型精度影响的缺陷。

（2）可以直接估计每一个观测量传播路径的电离层延迟量，不需要对电离层建模。

（3）由于参数的相关性，设备时延、初始相位叠加到接收机钟差、电离层延迟和模糊度参数之中，这说明数据处理时不需要特别考虑设备时延或码间偏差问题，而在传统的单频定位中，必须对该项进行改正。

在静态定位试验中，各测站高程方向的误差存在明显的系统误差特性，其原因还有待进一步研究。

［1］ BERAN T，KIM D，LANDLEY R B.High－Precision Single－Frequency GPS Point Positioning［C］∥Proceedings of ION GPS／GNSS 2003.Portland：［s.n.］，2003：1192－1200.

［2］ CHOY S，ZHANG K，SILCOCK D.An Evaluation of Various Ionospheric Error Mitigation Methods Used in Single Frequency PPP［J］.Journal of Global Positioning Systems，2008，7（1）：62－71.

［3］ GAO Yang，ZHANG Yufeng，CHEN Kongzhe.Development of a Real－Time Single－Frequency Precise Point Positioning System and Test Results［C］∥Proceedings of the 19th ION GNSS 2006.Fort Worth：［s.n.］，2006：2297－2303.

［4］ MONTENBRUCK O.Kinematic GPS positioning of LEO Satellites Using Ionosphere－free Single Frequency Measurements［J］.Aerospace Science and Technology，2003，7（5）：396－405.

［5］ MUELLERSCHOENM R J，IIJIMA B，MEYER R，et al.Real－Time Point－Positioning Performance Evaluation of Single－Frequency Receivers Using NASA＇s Global Differential GPS System［C］∥Proceedings of ION GNSS 2004.Long Beach：［s.n.］，2004：1872－1880.

［6］ ZHANG Xiaohong，LI Xingxing，GUO Fei，et al.Realization and Precision Analysis of Single－Frequency Precise Point Positioning Software［J］.Geomatics and Information Science of Wuhan University，2008，33（8）：783－787.（张小红，李星星，郭斐，等.GPS单频精密单点定位软件实现与精度分析［J］.武汉大学学报：信息科学版，2008，33（8）：783－787.）

［7］ SONG Weiwei，SHI Chuang，YAO Yibin，et al.Ionospheric Delay Processing Methods and Positioning Precision of Single Frequency Precise Point Positioning［J］.Geomatics and Information Science of Wuhan University，2009，34（7）：778－781.（宋伟伟，施闯，姚宜斌，等.单频精密单点定位电离层改正方法和定位精度研究［J］.武汉大学学报：信息科学版，2009，34（7）：778－781.）

［8］ CHEN Kongzhe，GAO Yang.Real－Time Precise Point Positioning Using Single Frequency Data［C］∥Proceedings of ION GNSS 2005.Long Beach：［s.n.］，2005.

［9］ YUNCK T P.Orbit Determination［R］.Reston：American Institute of Aeronautics and Astronautics，1996.

［10］ TU Rui，ZHANG Qin，HUANG Guanwen.On Ionospheric Delay Processing Methods for Single Frequency Precise Point Positioning［J］.Journal of Geodesy and Geodynamics，2010，30（2）：99－103.（涂锐，张勤，黄观文.单频精密单点定位电离层延迟处理方法研究［J］.大地测量与地球动力学，2010，30（2）：99－103.）

［11］ KLEUSBERG A，TEUNISSEN P J G.GPS for Geodesy［M］.Berlin：Springer－Verlag，1996.

［12］ CHEN Yi.The Model of Single－point Positioning by Use Ephemeris and Result Analysis［J］.Acta Geodaetica et Cartographica Sinica，2002，31（Sup.）：31－33.（陈义.利用精密星历进行单点定位的数学模型和初步分析［J］.测绘学报，2002，31（增刊）：31－33.）

［13］ KOUBA J.A Guide to Using International GPS Service（IGS）Products［EB／OL］.［2008－09－15］.ftp：∥igscb.jpl. nasa.gov／igscb／resource／pubs／GuidetoUsingIGSProducts.pdf.2003：31.

［14］ BIERMAN G J.Fractorization Methods for Discrete Sequential Estimation［M］.New York：Academic Press，1977.

［15］ SONG Lijie，OUYANG Guichong.A Fast Method of Solving Partitioned Adjustment for Super Large－scale Geodetic Network［J］.Acta Geodaetica et Cartographica Sinica，2003，32（3）：204－207.（宋力杰，欧阳桂崇.超大规模大地网分区平差快速解算方法［J］.测绘学报，2003，32（3）：204－207.）

［16］ TIBERIUS C C J M.Recursive Data Processing for Kinematic GPS Surveying［M］.Delft：NCG Nederlandse Commissie voor Geodesie Netherlands Geodetic Commission，1998.

［17］ YANG Yuanxi.Adaptive Navigation and Kinematic Positioning［M］.Beijing：Surveying and Mapping Press，2006.（杨元喜.自适应动态导航定位［M］.北京：测绘出版社，2006.）

［18］ YANG Yuanxi，HE Haibo.Sequential Least Squares Estimator for Solving Ambiguity of Kinematic GPS Phase Measurement［J］.Geomatic Science and Engineering，2005，25（1）：1－4.（杨元喜，何海波.GPS动态测量中模糊度实数解的序贯最小二乘估计［J］.测绘科学与测绘工程，2005，25（1）：1－4.）

［19］ TAPLEY B D，SCHUTZ B E，BORN G H.Statistical Orbit Determination［M］.Burlington：Elsevier Inc.，2004.

［20］ RUAN Rengui.Study on GPS Precise Point Positioning Using Un－differenced Carrier Phase［D］.Zhengzhou：Information Engineering University，2009.（阮仁桂.GPS非差相位精密单点定位研究 ［D］.郑州：信息工程大学，2009.）

［21］ RUAN Rengui，WU Xianbing，FENG Laiping，et al.Single－Frequency Precise Point Positioning Algorithm Based on Satellite Differential GRAPHIC Observables［J］.Journal of Geomatics Science and Technology，2012，29（1）：24－27.（阮仁桂，吴显兵，冯来平，等.星间差分GRAPHIC观测量单频精密单点定位算法［J］.测绘科学，2012，29（1）：24－27.）

E－mail：rrg2002me＠163.com

Single－Frequency Precise Point Positioning with Simultaneous Ionospheric Delay Estimation

RUAN Rengui1，WU Xianbing1，FENG Laiping1，WANG Xiwei2
1.Xi’an Research Institute of Surveying and Mapping，Xi’an 710054，China；2.78155 Troops，Chengdu 610036，China

A new method for single－frequency precise point positioning using code and phase measurement is presented.Ionospheric delay in each code and phase measurement is estimated as unknown parameters together with receiver clock offset，tropospheric zenith path delay，receiver position and ambiguity of carrier phase.Modified square root information filtering ＆smoothing algorithm with parameter elimination was employed for parameter estimation.The method can be applied to real－time positioning and post processing，and it is independent of any ionospheric model.With the method，static positioning test was carried out with GPS data collected at 32 stations of the International GNSS Service（IGS）through day 75 to90in2011，which shows RMS in E，N，U are0.023 m，0.018 m and0.059 m respectively.Kinematic experiment with airborne GPS data collected on September 5th 2008 shows that RMS in E，N，U compared with kinematic relative differential solution are 0.168 m，0.151 m and0.172 m.

single－frequency precise point positioning；ionospheric；delay estimation；parameter elimination；square root information filtering；square root information smoothing

RUAN Rengui（1983—），male，research assistant，majors in GNSS precise positioning and orbit determination.

RUAN Rengui，WU Xianbing，FENG Laiping，et al.Single－Frequency Precise Point Positioning with Simultaneous Ionospheric Delay Estimation［J］.Acta Geodaetica et Cartographica Sinica，2012，41（4）：490－495.（阮仁桂，吴显兵，冯来平，等.同时估计电离层延迟的单频精密单点定位方法［J］.测绘学报，2012，41（4）：490－495.）

P228

A

1001－1595（2012）04－0490－06

国家自然科学基金（141074020）；中国卫星导航学术年会资助

宋启凡）

2011－10－17

2012－01－16

阮仁桂（1983—），男，助理研究员，研究方向为GNSS精密定位和精密定轨。