既有铁路隧道衬砌裂损维修决策研究

李 云，吴小萍，廖群立

(中南大学土木建筑学院，湖南长沙410075)

0 引言

随着我国交通事业的迅猛发展，修建的隧道数量也越来越多.但是由于水文调查、地质、设计、施工、监理、验收、老化等各方面的原因，导致既有铁路隧道出现衬砌结构变形、开裂、错台、渗漏水、腐蚀等病害，隧道维修必将成为隧道研究热点.因此，根据隧道衬砌裂损情况，建立一种包括各种因素在内的决策评价体系，实现方案选择的定量化与最优化，具有现实意义.

粗糙集理论是由波兰数学家 Z.Pawlak于1982年提出的一种数据分析理论，其特点是不需要提供除问题所需处理的数据集合之外的任何先验信息，仅对实测数据本身进行分类处理，揭示内部规律，因而该方法对不确定性问题的处理相对客观［1］，粗糙集定权能保证权重系数的真实性和准确性.灰色理论是由华中科技大学学者邓聚拢1982年提出并创立.该理论以部分信息已知，部分信息未知的“小样本”、“贫信息”为研究对象，主要通过对部分已知信息生成、开发、提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效控制［2－5］.

既有铁路隧道衬砌维修方案所获得的指标数据往往具有离散、模糊和信息少等特征.笔者结合粗糙集与灰色理论处理此种不确定型复杂系统，具有互补性、真实性和准确性等特点.同时，专家评判定权法的引入，使评价结果更加适合于现实需要.

1 建立指标体系

既有铁路隧道衬砌维修决策指标涉及多个领域.笔者将决策指标按其属性进行分类，形成层次结构.第一层，总目标层，用U表示;第二层为子目标层，由经济性、施工方便程度、施工文明程度、质量保证四项组成，分别用 U1、U2、U3、U4表示;第三层为指标层，由成本(u11)、技术要求(u21)、工期(u22)、列车运营的影响(u23)、设备要求(u24)、次级灾害的可能性(u31)、列车对人的影响(u32)、噪声与环境污染(u33)、工作安全程度(u34)延长的使用年数(u41)等10项组成.各层之间的隶属关系如图1所示.

2 指标权重的建立

建立知识表达系统 s=(U，A，V，f)，并且采用等频率区间法进行离散得到离散值.其指标均离散化为 4 个值：1，2，3，4.分别代表差、一般、良、优［2］.

根据离散值分别计算每个子目标知识表达系统的可辨识矩阵［4］M=(mij)n×n，其中，

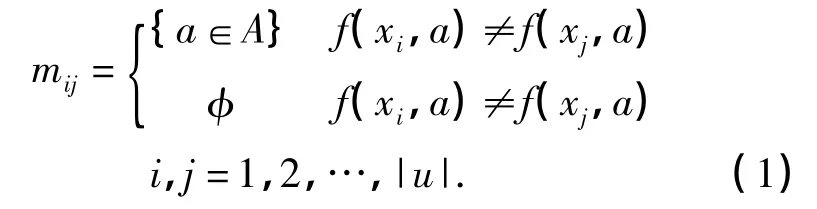
图1 铁路隧道衬砌维修决策综合评价指标体系Fig.1 Railway Tunnel Lining Maintenance Decision comprehensive evaluation index system

根据文献［1－4］可知，指标出现的频率越高，其潜在的区分能力也越大，但这种频率的计算不是简单的计算，而是加权的，加权的大小根指标出现的分辨矩阵中的长度有关.对于分辨矩阵，其重要度记为w(a)，计算公式为［5］

每个子目标下的指标计算所得重要度归一化，既得指标权重，其中表示包含a的个数.如果指标a的重要度为0，则表示可以将a约简，否则不可约，最后可得到指标的权重向量 wi，i=1，2，…，n.同时，在此基础上结合专家判断法得到隧道衬砌裂损维修方案决策的子目标权向重 w［3－9］.

3 决策排序

3.1 确定评价灰类

离散值可作为灰数的白化值.确定评价灰类就是要确定灰类的灰数，等级数及白化权函数.笔者采用4 个评价灰类，灰类序号为e，e=1，2，3，4，分别表示“优”、“良”、“一般”、“差”，其对应的白化权函数如下［6－7］：

第一灰类“优”(e=1)，设定灰数⊗1∈［4，+∞)，可得白化权函数为f1的表达式如下：

第二灰类“良”(e=2)，设定灰数⊗2∈［0，6)，可得白化权函数为f2的表达式如下：

第三灰类“一般”(e=3)，设定灰数⊗3∉［0，4)，可得白化权函数为f3的表达式如下：

第四灰类“差”(e=4)，设定灰数⊗4∈［0，2)，可得白化权函数为f4的表达式如下：

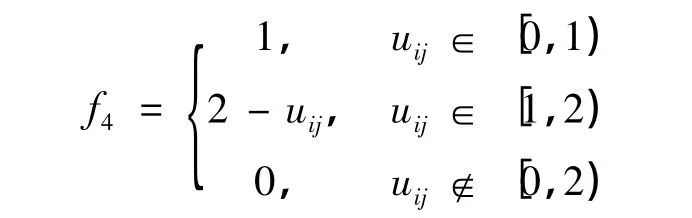
3.2 计算灰类评价权向量及矩阵

对评价指标uij，第s个方案的总灰类评价系数记为.对第s个方案的第e个灰类的灰色评价权记为.

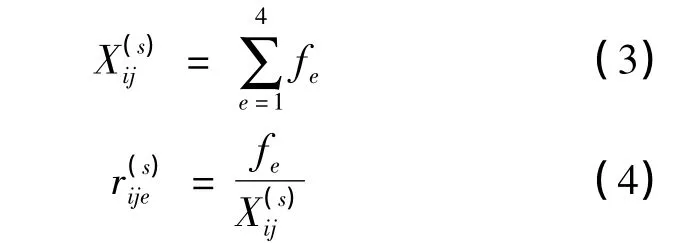
每个指标由4个灰类的评价权组成，因此，第s个方案的评价指标uij对于灰类的灰色评价权向量为［10］

将第s受评方案的Ui的所属指标uij对于评价灰类的灰色评价权向量综合后，获得第s个受评方案Ui所属指标uij对于各评价灰类的灰色评价权矩阵

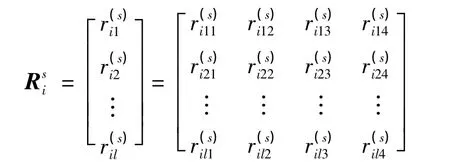
3.3 对Ui进行评价

对于第s个受评方案的Ui作综合评价，其综合评价结果可记为则有：

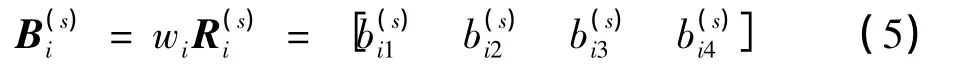
由Ui得综合评价结果得到第s个受评方案所属指标Ui对于各评价灰类的灰色评价矩阵

对第s个受评方案的U作综合评价，其综合评价结果记为B(s)，则有：

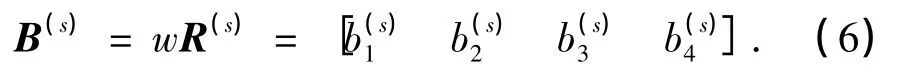
3.4 计算综合评价值

综合评价结果B(s)为向量，无法用于决策结果排序.因此需做一定处理，笔者引入不同灰类的权系数cj(j=1，2，3，4)，使结果单值化.可事先确定数值(c1=4，c2=3，c3=2，c4=1).

则第s个受评方案的综合评价值为U(s)［3］

根据计算结果值从大到小排序，数值最大者为最优方案.

4 模型应用

思蒙四号隧道于1971年2月建成，全长201.7 m，位于湘黔线溆浦和仁里冲区间.该地雨水充足，雨量受季节影响较大.隧道围岩为泥质板岩，裂隙和风化都比较严重.调查表明，思蒙四号隧道进口至洞标80 m拱部裂损掉块，段标130～201 m衬砌边墙拱部均严重裂损，出口左侧洞门受山体挤压开裂外倾，产生的错台在变化中，右边边墙外突产生变形，其裂纹宽度和长度还在不断加大，影响衬砌稳定性.隧道内裂纹较多，漏水严重，接缝处水流较大等.笔者选取其中一段作为维修决策分析，此段主要病因是：围岩长期受水的侵蚀出现部分松动、隧道衬砌受到偏压、渗漏水严重等.根据病害状况制定如下4个维修方案：方案一：锚杆+注浆(u1)，方案二：挂网+注浆(u2)，方案三：挂网+安装排水管/槽(u3)，方案四：注浆(u4).根据相关专家的分析与实际情况结合等频率区间法得指标层的离散化如表1所示.

根据可辨识矩阵的启发式约简算法公式(1)，(2)分别算出重要度，归一化得指标层的权重 w1=(1)，w2=(0.305 6，0.194 4，0.277 8，0.222 2)，w3=(0.222，0.222 2，0.361 1，0.194 4)，w4=(1)

根据隧道实际情况，在启发式约简算法的基础上结合专家判断法得到隧道衬砌维修决策的总目标权重：w=(0.2，0.3，0.15，0.33)

表1 指标层离散化表Tab.1 Indicators layer of discrete form

限于篇幅，笔者以方案一为例，根据方案一的离散值，结合白化权函数与式(3)～(5)可得灰色评价矩阵：

根据式(6)可求出第1个受评方案的综合评价结果向量B(1)：

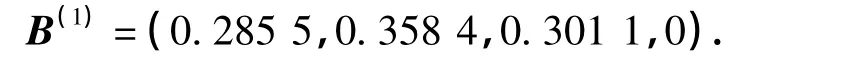
根据式(7)可得第1个受评方案的综合评价值为U1=2.983 5，同理，可得方案二、方案三、方案四的综合评价值分别为，U(2)=2.885 3，U(3)=2.953 8，U(4=2.964 4，U(1)=2.983 5.故方锚杆+注浆为最优方案，这与实际运用的治理方法相符.

5 结论

(1)笔者采用可辨识矩阵启发式约简算法对指标层进行定权，采用专家评判法对子目标定权，这样既可以保证权重的客观性、准确性和真实性，又能保证权重符合现实需要，使权重更加有效、合理.同时，笔者采用灰色理论中的多层次灰色综合评价法对既有铁路隧道衬砌维修方案进行综合决策，解决了“小样本”或“贫信息”方案难以评价的问题，又保证了决策结果的真实性.而思蒙四号的实例应用表明，该方法可定量的得出所需结果，具有一定的推广价值.

(2)结合实际情况，笔者运用几种不同的数学方法，将定量和定性有机结合，从不同角度研究既有铁路隧道衬砌维修方案决策模型.几种数学方法的综合运用，为同类工程提供了借鉴意义.

［1］吴其刚，杨建军，高明明.城际铁路建设准入室序决策模型研究［J］.铁道工程学报.2009(10)：102－105.

［2］芦晓红，陈世权，吴今培.基于可辨识矩阵的启发式属性约简方法及其应用［J］.计算机工程.2003，29(1)：56 －58.

［3］罗冠枝，徐林荣.基于粗糙集和灰色理论的模糊综合定权法在泥石流危险性评价中的应用［J］.安全与环境工程.2008，15(3)：1 －6.

［4］史成东，陈菊红，郭福利.基于粗糙集的供应链绩效改进决策研究［J］.计算机工程与应用.2007，43(32)：185 －187.

［5］石骁，赵庆飞.基于粗糙集理论的模糊综合评判权值确定［J］.西南石油学院学报.2001，23(3)：16 －19.

［6］孙楠，姚林，孙峥.城市生态安全多层次灰色综合评价［J］.中国安全科学学报.2008，18(2)：143 －148.

［7］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用［M］.北京：科学出版社，2005.

［8］苗夺谦，李国道.粗糙集理论、算法与应用［M］.北京：清华大学出版社，2007.

［9］匡乐红，徐林荣，刘宝琛.组合赋权法确定地质灾害危险性评价指标权重［J］.地下空间与工程学报.2006，2(6)：1063 －1067.

［10］杨俊辉.高校毕业设计(论文)质量的多层次灰色评价方法研究［J］.西南邮电学院学报.2008，13(3)：153－157.