椭球壳及椭球体转动惯量的简易推导

刘 红

（北京物资学院物流学院，北京 101149）

椭球壳及椭球体转动惯量的简易推导

刘 红

（北京物资学院物流学院，北京 101149）

本文利用微积分方法，给出计算球壳、球体转动惯量的一种简易办法，又利用正交轴定理，给出椭球壳、椭球体的转动惯量.

转动惯量；球壳；球体；椭球壳；椭球体

在讲授《大学物理》刚体绕定轴转动时，要向同学们介绍一个新的概念：转动惯性的量度，即转动惯量.在中学阶段，同学们没有接触过这个概念，大学阶段需要讲解清楚，一般教科书都会列出几种常用刚体的转动惯量［1］，然后以例题的形式给出均质细杆、均匀圆环和圆筒及均质圆盘和圆柱体的转动惯量的推导，但对球壳和球体的转动惯量的推导基本不提，似乎是让学生自己练习得到.从维数的角度看，球壳、球体属于三维，比起二维的圆环、圆盘难度高了一个数量级.用高难度的题作练习，不符合学生的实际能力，往往效果不佳，留下一个漏洞，让学生觉得大学物理很难，没有思路，无从下手，即使勉强做了，发现和答案不一样，自己找不出错误的原因，不知是书上给错了呢，还是自己推导错了，这种疑虑对大学物理学的教学产生不利影响.

本文通过简单的推导，让学生觉得，自己通过学习，把数学知识用到物理的具体过程，发现自己在推导过程中本事变大了，事半功倍.下面就用微积分的思想，给出让圆环长大变成球壳，让球壳长大变成球体，给出球壳、球体的转动惯量，然后延伸到椭球壳、椭球体的转动惯量，开阔学生眼界，起到交流的作用.

1 让圆环长大变成球壳

物理中的圆环是一个理想的圆环，质量为M，半径为R，质量均匀分布，即均质，其线密度λ的定义为单位长度上的质量，因为均质，所以任何在该线上的一小段，都具有相同的λ.圆环转动惯量的表达式为

现在让圆环长大，先让一个质量为M，半径为R的大圆环向上长，长成半个球壳，之后乘2得整个球壳.成长中的圆环，质量在变，半径在变，变到半个球壳时，用积分形式表示如下

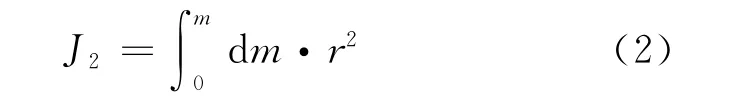
如何把变量dm与变量r联系在一起呢？用理想均质圆环的线密度作过渡

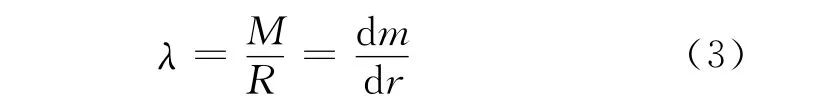
将式（3）中的dm代入式（2），积分后就得到半个球壳绕中心轴的转动惯量

对式（4）乘2，就得整个球壳的转动惯量

2 让球壳长大变成球体

有了球壳的表达式，球体可以看成是一个半径很小的球壳，沿半径的方向长大，长到半径为R停止，成长中的球壳，质量在变，半径在变，变到一个球体时，用积分形式表示如下

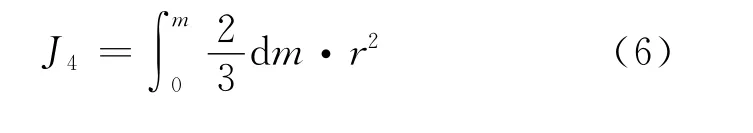
如何把变量dm与变量r联系在一起呢？用理想均质球体的体密度作过渡，球体从小长大的过程中，体密度保持不变，体密度用ρ表示，其定义为单位体积内的质量，局部和整体一致

将式（7）中的dm代入式（6）中，积分后可得球体的转动惯量

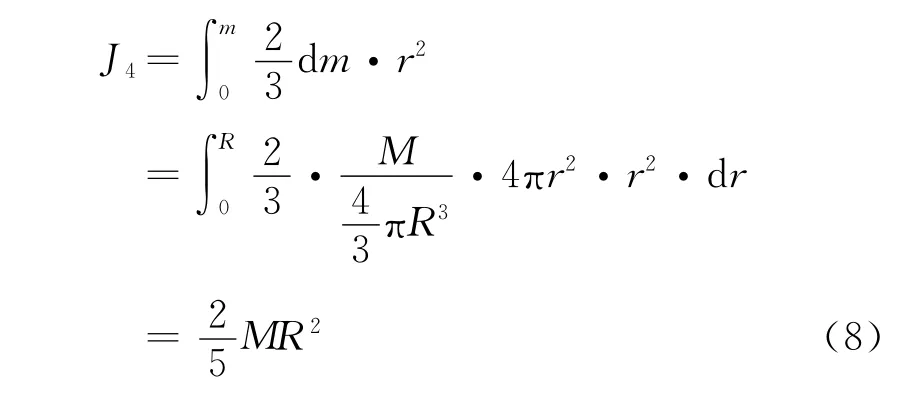
此种方法被普遍应用，是微积分精彩范例之一.

3 让球壳变成椭球壳

把球壳压扁一点，对称性稍有破坏，它的转动惯量如何求呢？我们用已经求得的绕固定轴转动惯量的表达式，通过转动惯量正交轴定理［2］，将对成轴z轴的转动惯量，分解到不对称的正交的x轴和y轴，

对于椭球壳，设x方向和y方向的半径分别为R1和R2，根据式（9），椭球壳的转动惯量为

当R1＝R2时，式（10）即为式（5），为球壳的转动惯量.

4 让球体变成椭球体

椭球体转动惯量的求法，可以按照以上对椭球壳求法的思路，将对称的轴分解成不对称的两个正交轴，半径分别为R1和R2，则椭球的转动惯量

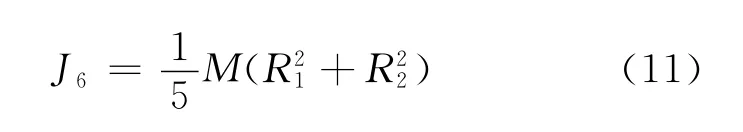
当R1＝R2时，式（11）即为式（8），为球体的转动惯量.

从以上推导可以看到微积分鲜活的生命力，给人形象生动的感觉.而正交轴定理又巧妙地简化了运算，如果不用正交轴定理，椭球壳和椭球体的求法有一定的计算量［3］.

［1］ 吴百诗.大学物理［M］（第三次修订本）.西安：西安交通大学出版社，91

［2］ 黄国集.益阳师专学报（自然科学版），1989，（2）52-55

［3］ 赵新闻，杨兵初，黄生祥.椭球体转动惯量的计算［J］.物理与工程，2007，（2）

2011-07-24；

2011-11-02）

刘红（1966年出生），女，湖北鄂州市人，博士，副教授，主要从事基础物理学的教学.