对匀速率曲线运动的解释＊

章 曦 李配军 吴方平 董秋云 马书云

（解放军理工大学理学院应用数学与物理系，江苏 南京 211101）

对匀速率曲线运动的解释＊

章 曦 李配军 吴方平 董秋云 马书云

（解放军理工大学理学院应用数学与物理系，江苏 南京 211101）

通过理论推导，给出了匀速率曲线运动的规律；同时将理论结果与数值计算进行对比，数值计算与理论吻合得很好.最后给出了控制匀速率曲线运动的方法.

匀速率曲线运动；运动的规律；运动的控制

在《对匀速率曲线运动的探讨》一文［1］（以下简称引文）中，笔者给出了不同情形下质点作匀速率曲线运动的轨迹.那么，质点作匀速率曲线运动的规律是什么呢？

1 理论与方法

t＝1s时刻，an＝0（见图3（a）），此瞬间质点作匀速直线运动；同样，t＝2s时刻，质点也是作匀速直线运动.这两条直线（见图1（d））之间的夹角就是第二秒内质点运动方向所转过的角度.考虑到函数形式的周期性，第n（n为1到30内任一正整数）秒内质点运动轨迹的切线方向所转过的角度φ是一样的.

下面来推导角度φ的具体值.考虑一段无穷小的时间间隔dt，这一段时间内质点转过的角度为ωdt，利用质点作曲线运动的性质［2］，得φ＝这里g＝an／v，与引文中的定义相同.取t1＝1s、t2＝2s，得：φ＝600／π，实际上就是曲线下第二秒内的面积S.

图1 不同时刻质点的运动轨迹

2 数值计算

接下来给出数值计算（这一工作在 Matlab［3］中完成）的结果，对理论结果进行验证.首先给出利用计算机求解φ值的方法.如图2，t＝1s时刻质点的运动方向可以用t＝0.999s时刻和t＝1.001s时刻质点位置所确定的直线来近似；同样的，t＝2s时刻质点的运动方向可以用t＝1.999s时刻和t＝2.001s时刻质点位置所确定的直线来近似.这样，就可以进一步计算出第二秒内质点所转过的角度φ.

图2 数值计算角度φ的方法

（2）式，参见图3（c）

对于这两种情形，对应于不同的C值，表1也给出了φ值（分别记为φ2和φ3）的数值计算结果.该结果与理论值也是相吻合的.

表1 不同情形下第二秒内质点转过的角度φ值的数值计算结果

图3 g的几种不同函数形式

3 结论与分析

值得注意的是，对于C的几种不同取值，φ3的取值为π或0（忽略数值计算的误差）.基于这一原理，我们可以对匀速率曲线运动进行控制.在引文中，g情形下，质点的运动轨迹是不闭合的，而我们只给出了30s内质点的运动轨迹.事实上，随着时间的演化，质点的运动轨迹会变得越来越复杂，艺术上的美感也会大大减弱.

这里，我们可以通过对g函数形式的限制来得到一个闭合的运动轨迹.比如取为式（2）的表达形式，其中C＝324.此时，质点的运动轨迹如图4（a）所示.这种情况下，质点的运动轨迹是闭合的；即使时间趋于无穷大，质点的运动轨迹依然保持不变.

通过参数的调节，我们可以得到任意数目的“漩涡”.当C＝319时，质点的运动轨迹如图4（b）所示.当C＝320＋8／7时，质点的运动轨迹如图4（c）所示；当C＝320＋8／9时，质点的运动轨迹如图4（d）所示.

注意到C＝321和C＝319时，质点的运动轨迹中的“漩涡”数同为8个，但运动轨迹有着细微的差别，C＝321时质点的运动轨迹类似于图4（c）和图4（d）（没有给出）.

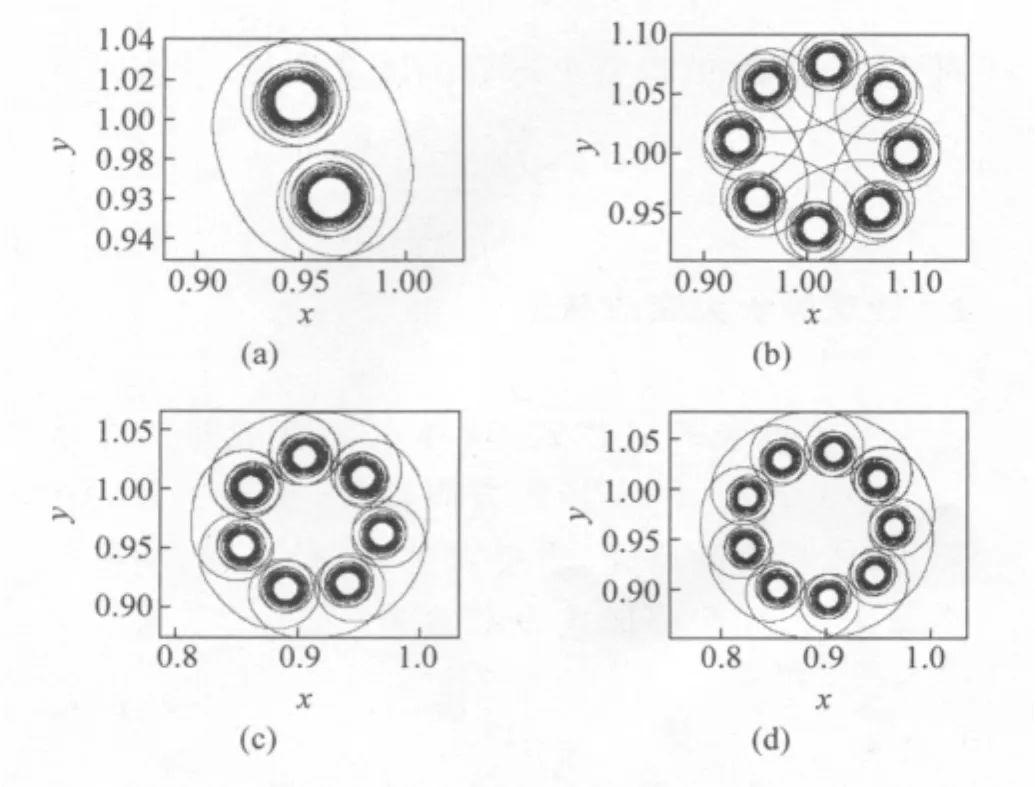
图4 对匀速率曲线运动的控制

［1］ 章曦等.对匀速率曲线运动的探讨［J］.大学物理，2009，28（6）：9～11

［2］ 周衍柏.理论力学教程［M］ 2版.北京：高等教育出版社，1986.3：17

［3］ 张志涌.精通 MATLAB6.5［M］.北京：北京航空航天大学出版社，2003.3

2011-05-31；

2011-09-27）

解放军理工大学理学院青年预研基金（QN-WL-2009-06）和解放军理工大学青年预研基金（20110521）资助.

章曦（1983年出生），男，安徽巢湖人，解放军理工大学理学院应用数学与物理系讲师，硕士，主要从事混沌神经网络和激光探潜方面的研究.