提高迈克尔孙干涉仪实验精度方法研究

董爱国 高 华 王亚芳 周惟公 张自力

（中国地质大学（北京）实验物理教学中心，北京 100083）

提高迈克尔孙干涉仪实验精度方法研究

董爱国 高 华 王亚芳 周惟公 张自力

（中国地质大学（北京）实验物理教学中心，北京 100083）

重点讨论了迈克尔孙干涉仪测量波长和波长差实验中的误差来源和影响因素，进一步提出了解决方法和改进方案，提高了测量精度.

迈克尔孙干涉仪；校准；空程差；视见度

迈克尔孙干涉仪作为重要的光学仪器，大学物理实验中往往用于激光的波长、钠光波长差以及透明介质的厚度或者折射率的测量.实验中影响测量精度的原因有很多，结合实验教学，从以下几个方面进行讨论.

1 空程差与仪器校准

空程差广泛存在于靠齿轮或螺旋（螺杆）传动的机构和仪器当中，其产生原理可由图1表示.由于螺纹或齿轮之间不能够完全啮合，当主动轮反向转动时，从动轮相对主动轮存在移动的滞后，我们称之为空程差［1］.其测量系统包括微动鼓轮、粗调手轮和主尺，鼓轮和手轮之间为螺旋传动，手轮和主尺之间为螺杆传动，为二级传动.其主尺固定，鼓轮和手轮可调：转动微动鼓轮时，手轮随着转动，但转动手轮时，鼓轮并不随着转动，故粗调手轮和微调鼓轮之间存在空程差；转动手轮时，主尺指示刻度也不一定发生变化，故手轮和主尺之间同样存在空程差，为二级空程差.

图 1

调节中，为了提高精度，在同一组测量中必须考虑螺纹的空程差，即只能沿同一个方向旋转微动鼓轮，所有的实验教材都很强调这一点，同时也为广大教学、科研工作者所认同［2～6］.但是，现有的方法基本上在指出消除空程差的时候，往往忽略了仪器的校准，或者虽然指出校准的方法，但是校准中忽略了空程差的影响，实际上并没有校准.常见的校准方法如下：将鼓励沿某一方向旋转至零，然后以同方向转动手轮使之对齐某一刻度.这以后，在测量时只能仍以同方向转动鼓轮［2～4］.

为讨论方便，用图2表示.容易发现，按此方法，调节微动鼓轮一圈后，会出现如图3所示的情况：虽然鼓轮和零刻度对齐，但手轮上指示刻度的标线并没有和下一刻度线对齐.显然，出现此情况的原因就在于：校准的时候由于旋转了手轮，手轮和鼓轮之间又产生了空程差.因此，并没有完成仪器的校准，必然会引起读数的问题，如出现无法读数的情况等.

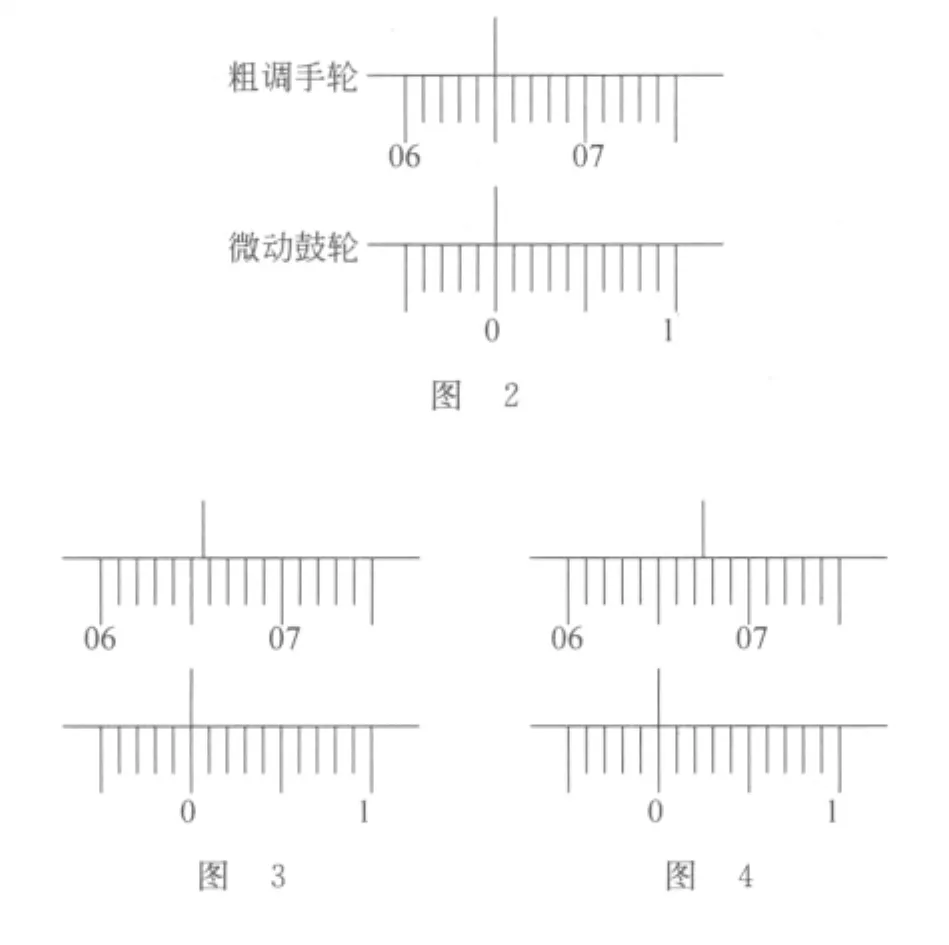
容易发现，图3中刻度线和标线的差值即为空程差，用Δx表示.可以进行如图4所示的操作：按原方向旋转手轮，使标线超出刻度线Δx.这样虽然手轮和鼓轮之间又会产生空程差，但是再旋转鼓轮一圈后，手轮刻度线前进0.01—Δx，则刚好和刻度线对齐，仪器完成校准，而此时手轮和鼓轮之间空程差也已经消除.因此，以后只要按原方向旋转鼓轮，直至观察到干涉条纹的吞吐现象，则手轮和主尺之间空程差也被消除掉.

当然，也可以将微调鼓轮调节到0.01－Δx位置上（按Δx约1／10格，则将鼓轮调节到9的位置上），再调节手轮和任一刻度线对齐，然后旋转鼓轮1.1圈，则手轮前进1格，和下一刻度线对齐，而此时手轮和鼓轮之间空程差也已经消除，继续旋转鼓轮一圈，则手轮又前进1格.

第三种方法，也是最简单的方法，在原方法“将鼓轮沿某一方向旋转至零，然后以同方向转动手轮使之对齐某一刻度”的基础上反方向转动鼓轮即可.因为按原方法反向不存在空程差.

需要指出的是，主尺和手轮之间也可能存在如图3所示的情形，但是因为主尺固定，所以主尺和手轮之间无法完成校准.则在测量中，主尺上的读数可以“随便读”：如图2所示，将手轮视为主尺，则此时主尺读作64、65、66均可，当手轮旋转超过零刻度线时，将主尺读数加1即可.

2 波长测量中条纹变化数目的确定方法

根据干涉理论：每变化一个条纹（如：明条纹变到暗条纹，如图5示从b到c），光程差变化量为λ／2，因 此 改 变 Δk条 条 纹 时，光 程 差 变 量 为Δk（λ／2）；若测量出镜子间距改变量Δd，可得光程差为2Δd，则有Δk（λ／2）＝2Δd，可得

图 5

但是习惯上一般采用如图5所示的从a到c，即变化一个级次的时候进行读数，显然若条纹变化数为Δk，级次变化数仅为Δk／2，令ΔK＝Δk／2，则有

3 叉丝定位与波长测量

叉丝与圆环相切位于如图5的a位置时测量数据见表1，叉丝位于b位置时测量数据见表2.

运用逐差法：

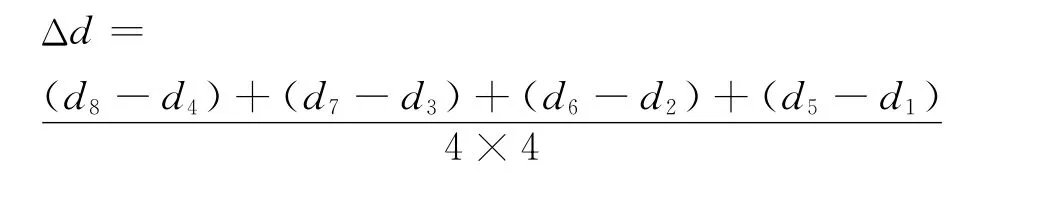
表1 激光波长测量记录表 （ΔK＝20）

表2 激光波长测量记录表 （ΔK＝20）

可 求 得 Δd 分 别 为：0.006 336 25mm、0.006 392 50mm，代入式（2）可得波长分别为：633.625nm、639.250nm.

可见，定位叉丝离中心越远偏差越大.因此，可以将“＋”十字叉丝改成“＝｜”双十字叉丝，测量时使上下横向的叉丝与圆环两端均相切，则可提高测量精度.

4 视见度周期性变化特征与测量方法研究

图 6

干涉仪测量波长差利用的是视见度周期性变化原理，光程差改变为镜子移动距离的2倍时，条纹的数目和间距发生周期性变化，如图6所示.波长差与镜子移动距离之间的关系为：实验中测量视见度变化一个周期所对应的镜子移动量Δd即可计算出波长差.但是，视见度变化存在一个问题：连续性变化.这样，在判断时很难界定是否“回到”了最初的视见度状态.实验中发现，调节鼓轮两三圈，视见度变化很小，而一个周期经计算大约为0.3mm，则测量误差大约在10%左右.这就带来了一个问题：测量时是否必须调节鼓轮呢？加以分析，则有多种测量方法.比如，方法一：采用调节手轮的方法，读数时直接在手轮上进行估读；方法二：先调节手轮再调节鼓轮，虽然有空程差，但可以忽略不计（在调零的过程中可以判断两个螺旋之间的空程差约为0.001mm）；方法三：只调节鼓轮进行测量.方法三应用较广泛，但比较耗费时间；方法一和二则可以提高测量的速度，如能够采用视见度变化多个周期（比如两个周期）时读数，则又可以保障测量的精度.

［1］ 董爱国，周惟公，张自力等.读数显微镜测量中系统误差的研究［J］.高等理科教育，2007年教育教学研究专辑：139～140

［2］ 丁慎训，张连芳.物理实验教程［M］.北京：清华大学出版社，2002.226

［3］ 刘路，周苒.迈克尔孙干涉仪定域干涉光程差和波长的讨论［J］.四川教育学院学报，2007，23（5）：111～112

［4］ 李雅丽，施建珍，袁莉等.多个等倾干涉条纹同时形成的理论与实验研究［J］.物理与工程，2007，17（4）：29～32

［5］ 戴彤炎，唐艳丽，孙晓娟.绘图仪传动回差分析与结构改进［J］.哈尔滨工业大学学报，2006，38（7）：1072～1074

［6］ 罗浩文.迈克耳孙干涉仪对空程差的测定［J］.实验科学与技术，2005年10月增刊：143、183

STUDY ON IMPROVEMENT METHOD OF
MICHELSON INTERFEROMETER EXPERIMENT PRECISION

Dong Aiguo Gao Hua Wang Yafang Zhou Weigong Zhang Zili

（Center of Experimental Physics Teaching，Geosciences University of China，Beijing 100083）

This paper emphasizes on the error source and influencing factors in the Michelson Interferometer experiment of measuring the wavelength and wavelength difference.Solutions and improved scheme are promoted to improve the experiment precision.

Michelson interferometer；adjustment；backlash error；percent articulation

2011-10-11；

2012-05-16）

董爱国（1976年出生），男，河北唐山人，助研，2000年毕业于中国地质大学（北京）信息工程学院，后从事自动化领域工作；2003年至今，在中国地质大学（北京）物理实验教学中心，从事实验技术、教学以及管理工作.