基于马尔可夫模型的交通枢纽客流集散方式研究

叶玉玲，王 浩

（同济大学 交通运输工程学院，上海 201804）

基于马尔可夫模型的交通枢纽客流集散方式研究

叶玉玲，王 浩

（同济大学 交通运输工程学院，上海 201804）

运用马尔可夫决策理论的系统状态转移矩阵决策法，分析交通枢纽客流集散方式中出租车、公交车、地铁、私家车及其他 5 种交通方式的客流变化趋势和规律，通过建立交通枢纽客流集散方式分担率预测模型，采用马尔可夫分析法对未来的客流变化进行预测。以某交通枢纽为例进行实证研究，预测未来年度交通枢纽各种集散方式的分担率，并根据预测结果进行分析，提出有关协调优化对策。

交通枢纽；客流集散；分担率；马尔可夫模型

0 引言

城市对外交通枢纽是城际交通与城市交通衔接的纽带，主要位于城市对外交通出入口处，如铁路车站、长途汽车站、机场等。许多大城市的综合交通枢纽集中了航空、铁路、地铁等多种交通方式，相互之间换乘便捷，旅客下车或下飞机后，足不出户就可以通过其他交通方式到达目的地[1]。近年来，我国综合客运枢纽建设方兴未艾，以上海、深圳等为代表的各大城市正在积极推进综合客运枢纽的建设、运营与管理。目前，我国交通枢纽建设存在的主要问题是各种交通方式各行其政，缺乏协调管理；多种交通方式混合占用交通设施资源，交通设施利用效率较低；交通规划对各类运输方式的衔接与换乘缺少前瞻性、综合性和整体化研究；土地供应支持不足等。

因此，为保证交通枢纽高效有序运营，科学地预测各种交通方式的客流集散分担率显得极为重要。只有在准确掌握客流变化规律的前提下，才能合理地进行交通枢纽设施与设备的规划和布局。实际上，由于客流影响因素的随机性和复杂性，使判断结果与实际客流状况存在较大的偏差[2]，交通枢纽的设施与设备运营效率并不高。

传统的预测方法对交通方式分担率的预测很难得到准确的结果，如长期趋势预测法。该方法是依据历史数据的变化规律对未来市场状况进行预测，但对交通方式分担率这个无确定变化规律的变量来说，就不太适用，又如各种类型的回归分析法。这些方法均未考虑不同交通方式之间的相互作用，因而在提高交通枢纽设施与设备运营效率的决策上有欠缺，有可能使预测和决策产生较大的误差。

为克服已有预测方法工作量太大或可靠性不高的缺陷，针对客流变化的随机性、影响因素的多样性和短期内影响因素的相对稳定性[3]，建立基于马尔可夫模型的交通枢纽客流集散方式分担率预测模型，以枢纽内各种换乘方式客流量的历史数据为基础，采用Matlab软件编程进行模型求解。

1 马尔可夫预测法的基本思想

马尔可夫过程是以其发现者俄国著名的数学家马尔可夫命名的[4]。在已知目前状态(现在)的条件下，未来的演变(将来)不依赖于其以往的演变(过去)。这种已知“现在”的条件下，“将来”与“过去”独立的特性称为马尔可夫性，具有这种性质的随机过程称为马尔可夫过程。时间和状态都是离散的马尔可夫过程称为马尔可夫链。马尔可夫链是根据系统状态之间的转移矩阵来描述一个随机动态系统未来的发展状况，转移概率则反映了各状态之间某种内在的规律性[5]。

了解客流的发展状态，不但要考察客流在现阶段所处的状态，还要考察客流在过去所处的状态。马尔可夫指出，“系统达到每一状态的概率仅与近期状态有关，在一定时期后马尔可夫过程逐渐趋于稳定状态而与原始条件无关”，这一特性称为“无后效性”[6]。由于交通枢纽客流集散方式的选择是一个动态过程，各交通方式客流量作为过程的行为特征量，其变化呈现随机过程的特点，而马尔可夫链可描述这种具有随机波动特点的动态过程。

2 交通枢纽客流集散方式分担率预测模型

2.1 市场调研

市场调研的目的是获取相关的信息资料，并且对所获得的资料进行科学的分析和合理的转化，为建立状态转移矩阵做准备[7]。具体来说，就是搜集交通枢纽最近 2个年度的总客流量及客流集散中各种交通方式的旅客人数；调查上一年度枢纽各集散方式的保留客流量和转移到其他交通方式客流量的情况。其中，旅客选择集散方式的行为受交通方式特性、消费者偏好和票价等因素的影响。

2.2 建立状态转移矩阵

一般地，首先考虑初始条件，S(j)为j年度该交通枢纽集散方式分担率的状态，S i(j)为j年度交通方式i在交通枢纽客流集散中的分担率，设当前状态(即j＝0)为：

第i种交通方式分担率Si(0)=Xi(0)/X，即

式中：Xi(0)为当前交通方式i的客流量，X为当前枢纽的总客流量。

此时第i种交通方式分担率与初始分担率及枢纽总客流量有关。同时，假定满足无后效性及稳定性假设，即P1i(1)＝P1i(2)＝…＝P。其中，P1i(1)为第 1年交通方式 1 转移到交通方式i的概率。

由于交通方式的选择具有动态变化性质，第i种交通方式下一年度(即j＝1)的客流量为：

可用矩阵式表达k年所有状态：[S1(k)S2(k)…SN(k)] = [S1(0)S2(0)…SN(0)]×P[k]：

式中：P[k]为k步状态转移矩阵。

2.3 求解马尔可夫预测模型矩阵

当满足稳定性假设时，有S(k)=S(0)×P[k]。这个公式称为已知初始状态条件下的交通方式分担率k步预测模型。对远期交通方式分担率的预测，就是当k→∞ 时，求S(k)的取值。

由于S(k)=S(0)×P[k]，limS(k)=S(0)×limP[k]。因此，在已知初始条件下求远期交通方式分担率就是求稳态概率矩阵。最后，通过 Matlab 软件编程进行矩阵求解，得出预测结果。

3 实证研究

某大城市交通枢纽客流集散方式有 5 种，分别为出租车、公交车、地铁、私家车和其他，已知该交通枢纽 2010年、2011年各种集散方式的客流量情况如表1 所示，2011年各种集散方式间的转移量如表2 所示。预测该交通枢纽 2012年及系统达到稳态时各种集散方式的客流分担率。为方便计算分析，以符号 A、B、C、D、E 分别代表出租车、公交车、地铁、私家车及其他 5 种交通方式类型。

由表1、表2 可知，出租车在 2010年的枢纽客流集散中分担了 1 200 万名旅客，2011年有 110 万名旅客从出租车转移至公交车、地铁和私家车等交通方式，同时有 95 万名旅客由公交车、地铁等交通方式转移至出租车。

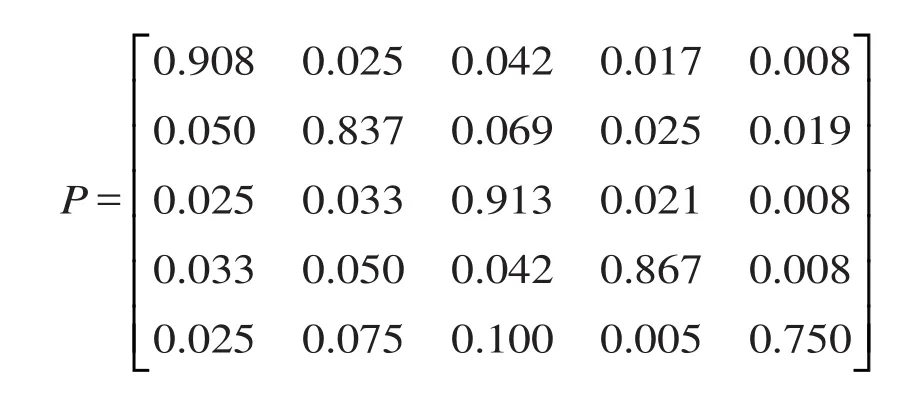
第一步：依据表1 数据计算得到马尔可夫转移矩阵。在该交通枢纽 2011年的客流集散方式选择中，出租车的概率PAA＝(1 200－110)/1 200＝0.908，出租车转向公交车的概率PAB＝30/1 200＝0.025，出租车转向地铁的概率PAC＝50/1 200＝0.042，出租车转向私家车的概率PAD＝20/1 200＝0.017，出租车转向其他方式的概率PAE＝10/1 200＝0.008。同理，可以计算出公交车、地铁等方式的客流分担率和转移概率。将上述计算结果按照对应的顺序排列，得到一步马尔可夫转移矩阵为：

表1 交通枢纽各种集散方式的客流情况 万人

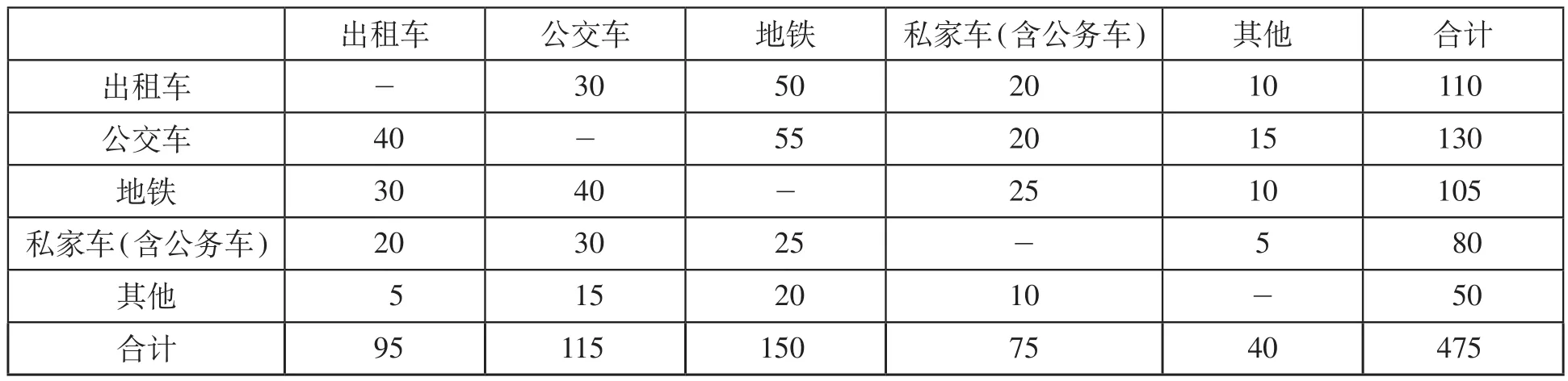
表2 2011年各种集散方式间的客流转移量 万人

第二步：计算 2011年该交通枢纽客流集散方式的状态概率。2011年出租车的分担率为PA＝1 265 / 4 300＝0.294；同理，公交车的分担率PB为0.204，地铁的分担率PC为0.302，私家车的分担率PD为0.151，其他方式的分担率PE为0.049。2011年该枢纽客流集散方式的状态概率为：

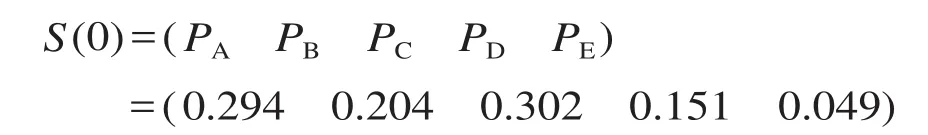
第三步：在该交通枢纽客流集散方式选择相对稳定的情况下，预测 2012年各种客流集散方式的分担率为：

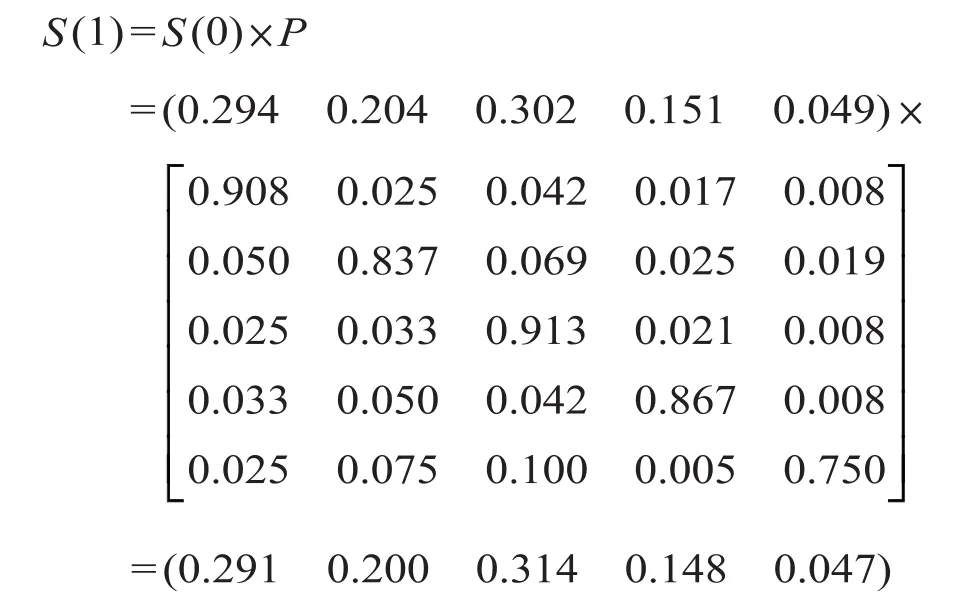
2012年在该交通枢纽的客流集散中，出租车、公交车、地铁、私家车及其他方式的分担率分别为 0.291、0.200、0.314、0.148 和 0.047。同理，可预测 2013年在该交通枢纽各种客流集散方式中，出租车、公交车、地铁、私家车及其他方式的分担率分别为 0.289、0.196、0.324、0.145 和0.046。

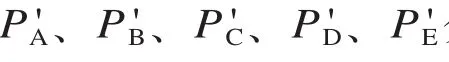
这表明，经过足够长的时间周期后，该交通枢纽的旅客集散方式选择处于一种稳定状态，其中选择出租车的旅客占客流集散总量的26.1%，公交车占 17.8%，地铁占 38%，私家车占 14.2%，而其他方式占 3.9%。

4 预测结果分析与对策

4.1 预测结果分析

（1）集散方式中地铁的客流分担率仍居首位，达 38%，且呈现上升趋势，上升速度比较快；出租车的客流分担率仅次于地铁，占 26.1%，仍居第二位，但是其降幅较大，应引起出租车运营方面的警觉，采取相应对策；公交车的客流分担率稍有下降，但基本保持原有份额。

（2）私家车和其他方式的客流分担率也稍有下降。这主要是因为城市公共交通在占用道路空间、环境污染和能源消耗 3 个方面具有优势，各大城市都在大力提倡和发展城市公共交通，使绿色环保低碳的公共交通出行方式成为城市出行的主要方式。

4.2 对策

针对该交通枢纽客流集散方式承担客运量的情况，城市交通运输管理部门需要协调优化各交通方式的分工，实现集散交通方式的协同运营、资源优化配置和交通安全协调应急指挥。

（1）缩短公共交通发车间隔的同时，发车时间尽量与枢纽内铁路旅客列车的到发时刻相匹配。由于轨道交通在枢纽客流集散中占有较大的分担率(算例中约占 38%)，因此在晚间轨道交通停止运营后应采取加大公交车的发车密度、开通夜间运营线路等措施，对夜间到发的旅客进行疏散。

（2）公共交通基础设施应满足旅客需求。一方面，缩短铁路客运站出入口至公交、轨道交通的换乘距离。公交枢纽一般应位于铁路客运站出入口附近，以便及时疏散集中到达的铁路客流；轨道交通规划设计也应与铁路车站设计相结合，缩短换乘距离，尽量使轨道交通的站厅或出入口靠近铁路站台及出入口，使旅客不用出站即可实现城市轨道交通与铁路的换乘。另一方面，公共交通标志应清晰合理。公共交通在设计标志和导向系统时应考虑色彩搭配和明暗光线设置，充分利用空间；地铁候车室的设计应注意宽敞简约，通常需要足够的灯光照明，且提供报纸、自动取款机等服务。

（3）提高服务质量。随着人民生活水平和消费能力的持续提高，未来旅客出行结构将会发生明显变化，消费性旅行需求的增长速度将会加快，旅客的多元化和个性化需求逐渐增加，旅客对公共交通方式的方便、快捷、舒适、安全等要求也会明显增强。因此，应树立以人为本、旅客至上的思想，转变服务观念，不断提高自身服务水平。

（4）枢纽交通行政管理体制的改革。建立由政府主导、市场协调的运营管理机构，形成畅通、安全、便捷的交通运输体系，改变条块分割、各自为政的交通管理模式，统筹各种运输方式的规划，明确枢纽从规划—建设—运营—管理各阶段相应的责任主体，进而与其他相关部门有效协调；整合各种交通资源，逐步推行决策、执行、监督相协调的大交通管理模式，以确保综合交通系统运营效益最大化[8]。

5 结束语

运用马尔可夫决策理论的系统状态转移概率矩阵决策法对交通枢纽客流集散中出租车、公交车、地铁、私家车及其他 5 种交通方式的客流变化趋势和规律进行分析，采用马尔可夫分析法对交通运输市场未来的客流变化进行预测。为解决铁路枢纽当前存在的主要问题，保证交通枢纽设施与设备高效有序运营提供了新的思路，并通过实例研究说明该方法的可行性。

：

[1] 王 南. 高速客运站设置的系统优化研究[D]. 成都：西南交通大学，2008.

[2] 杨新苗，王 炜，顾维平，等. 公交线路客流模糊神经网络预测模型[J]. 公路交通科技，2000，17(4)：43-46.

[3] 沈家军，王 炜，陈 俊. 基于灰色马尔可夫模型的近期公交客流量预测[J]. 公路交通科技，2007(9)：120-123.

[4] 林晓言，陈有孝. 基于灰色—马尔可夫链改进方法的铁路客运量预测研究[J]. 铁道学报，2005，27(3)：15-19.

[5] 梅振宇，王 炜，李 铭，等. 高速公路交通生成预测的改进灰色马尔可夫模型[J]. 公路交通科技，2004，21(12)：89-92.

[6] 傅广军. 现代企业管理与分析方法[M]. 北京：兵器工业出版社，1993.

[7] 蒋飞翔，孙有信. 马尔可夫分析法在旅客运输市场中的应用[J]. 交通科技与经济，2011(5)：100-102.

[8] 蔡昌淼，刘少波，付百学，等. 中心城市综合交通枢纽问题分析及对策[J]. 交通科技与经济，2010，12(6)：57-60.

Study on Passenger Flow Centralization and Distribution Mode in Traffic Hub based on Markov Model

YE Yu-ling,WANG Hao

(School of Traffic and Transportation,Tongji University,Shanghai 201804,China)

By using the system transfer matrix decision-making method in Markov decisionmaking theory,this paper analyzes the passenger flow change trend and principle of taxi,bus,metro,automobile and other traffic modes in passenger flow centralization and distribution mode of traffic hub. Through establishing the share rate forecast model of the mode,the passenger flow change in future could be forecast by using Markov analysis method. Taking the traffic hub as demonstration example,this paper forecasts the share rate of each centralization and distribution mode of traffic hub in future year and analyzes its forecast result,then puts forward relative coordination and optimization countermeasures.

Traffic Hub; Passenger Centralization and Distribution; Share Rate; Markov Model

1003-1421(2012)12-0048-05

U491.1+23；O211.62

A

2012-08-27

2012-10-22

何 莹